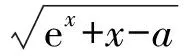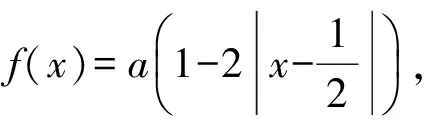利用f(f(x))=x根的性质巧解2道高考题

●

(南昌市外国语学校 江西南昌 330025)

利用f(f(x))=x根的性质巧解2道高考题

●梁懿涛

(南昌市外国语学校 江西南昌 330025)

( )

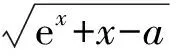
A.[1,e] B.[e-1-1,1]

C.[1,e+1] D.[e-1-1,e+1]

(2013年四川省数学高考理科试题第10题)

(2)若x0满足f(f(x0))=x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点，如果f(x)有2个二阶周期点x1,x2,试确定a的取值范围；

(3)对于第(2)小题中的x1,x2和a，设x3为函数f(f(x))的最大值点，A(x1,f(f(x1)))，B(x2,f(f(x2)))，C(x3,0)，记△ABC的面积为S(a)，讨论S(a)的单调性．

(2013年江西省数学高考理科试题第21题)

这2道试题不约而同地利用二阶迭代函数y=f(f(x))的不动点，即f(f(x))=x的根来命题．因为

f(f(x0))=x0⟺f(x0)=f-1(x0)，

(1)

所以原问题可以转化为y=f(x)与y=f-1(x)的交点问题，从而得到试题的简易解法(注：式(1)处f-1(x0)表示满足f(x)=x0的任意x)．

解答2道试题前，笔者先给出以下4个引理：

引理1函数y=f(x)与它的反函数y=f-1(x)图像的交点，或者在直线y=x上，或者关于直线y=x对称地成对出现．

证明设(a,b)是y=f(x)与y=f-1(x)图像的交点，即

从而

即(b,a)也是y=f(x)与y=f-1(x)图像的交点．显然点(a,b)与点(b,a)关于直线y=x对称,特别地，当a=b时，点(a,b)与点(b,a)重合在直线y=x上．

引理2如果函数y=f(x)是单调递增函数，那么y=f(x)与它的反函数y=f-1(x)图像的交点必定在直线y=x上．

证明由引理1，假如y=f(x)与y=f-1(x)的图像存在不在直线y=x上的交点(a,b)，则(b,a)也是它们交点，从而

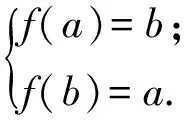
若a>b，则由y=f(x)单调递增，得f(a)>f(b)，即b>a，矛盾；同理若ab，也矛盾,从而假设不成立，y=f(x)与y=f-1(x)图像的交点必定在直线y=x上．

引理3若x0，f(x0)使得f(x0)及f(f(x0))有意义，且x0满足f(x0)=x0，那么x0也满足f(f(x0))=x0．

证明若f(x0)=x0，则f(f(x0))=f(x0)=x0成立．

引理4如果函数y=f(x)是单调函数，且存在x0，使得f(f(x0))=x0，则f(x0)=x0．

证明只需证明y=f(x)单调递增的情形，y=f(x)单调递减的情形同理可证．

假设f(x0)≠x0.若f(x0)>x0，则f(f(x0))>f(x0)>x0，与f(f(x0))=x0矛盾；若f(x0)

再运用以上4个引理来解答例1和例2：

ex+x-x2=a．

令φ(x)=ex+x-x2，x∈[0,1]，则

φ′(x)=ex+1-2x.

再令h(x)=ex+1-2x，则

h′(x)=ex-2，

显然h(x)在[0,ln2]上单调递减，在[ln2,1]上单调递增.因此

h(x)≥h(ln2)=3-2ln2>0，

即φ′(x)>0，于是

φ(x)∈[φ(0),φ(1)]=[1,e]，

即a∈[1,e]．故选A.

对例2的分析(1)略；

由f(f(x))=x，得f(x)=f-1(x)．结合引理3和引理4，得

解得

(以下同标准答案，略．)