浅谈中考数学复习课的选题策略
●
(丰北中学 浙江余姚 315400)
●陈立彬
(天台县教育局教研室 浙江天台 317200)
浅谈中考数学复习课的选题策略
●陈永浩
(丰北中学 浙江余姚 315400)
●陈立彬
(天台县教育局教研室 浙江天台 317200)
纵观近几年全国各地的中考试卷,多数能面向全体、注重基础、着眼未来,有利于引导正确的、积极的教与学;有利于学生掌握必要的数学基础知识、基本技能和基本思想方法;有利于面向全体学生以成功者的心态走向后续的学习和生活;有利于高中教育的普及与学生的可持续发展;能以知识技能应用为载体,以学生日常数学学习中的任务再现为背景,让学生重新经历数学学习的过程,重现过程性目标和结果性目标评价功能的融合、基础性目标和发展性目标评价功能的有机结合.中考卷是以“面向全体、注重基础、着眼未来”为原则,突出对学生基本数学素养的评价,注重学生在学习数学和应用数学解决问题过程中最为重要的、必须掌握的核心观念、思想方法、基本知识、基本活动能力和常用技能的考查,重视数学理性精神和继续学习能力的考核,注重过程评价,力求“为激励正确的、积极的教与学而考,为矫正教与学中存在的问题而考,为促进学生的可持续发展而考……”[1].
充分了解中考试题的特点,能较好地引导我们的复习工作,明确方向,把握重点、难点,提高复习效益.在平时的课堂教学中,教师应该合理地选取例题,尤其是应结合不同的教学要求,精心选取例题,让所有的教学行为紧紧围绕相应的教学目标(知识目标、思想方法目标、能力目标等),从而提高课堂教学的针对性和有效性,使教学效益达到最大化.下面从如何精选例题的角度谈谈中考复习课的选题策略,其中所举例题皆属笔者原创题,以期对同行有一定的参考价值.
1 以基础知识为核心,精选例题
“基础知识是学生学习的主要内容,学生需要掌握的数学学科知识”在《课程标准》中有非常明确的规定,同时从学生长远发展的角度看,教师还需关注数学学科以外的知识,真正完成数学学科所承担的教学任务和教育功能.
1.1 数学学科知识
数学学科知识是学生应掌握的基础知识.在课堂教学中,教师应讲清数学概念的本质,让学生充分地明白数学知识形成的过程是自然的;在数学概念的学习过程中,不仅要搞清楚是什么,更要搞清楚为什么,它的科学性、合理性、优越性在哪儿等等.

图1
例1对于2个平面图形甲和乙,点M,N分别是图形甲和乙上的任意一点,我们将线段MN长度的最大值定义为图形甲与乙的“通距”.如图1所示,⊙O1与⊙O2的“通距”应定义为
( )
A.线段BC的长度 B.线段O1O2的长度 C.线段O1C的长度
D.线段AD的长度
评析此题是学生由已学知识通过类比、迁移,自我构建新概念的过程,引导学生关注数学本质,明白数学是自然的、合理的.
1.2 社会生活常识
数学来源于生活实践,而又服务于生活实践,因此数学是有用的、有趣的.生活中的许多问题本身就是数学问题,它是编制数学试题的广阔题材.因此在课堂教学的例题中,应充分关注数学在生活实践中应用,提高学生的学习兴趣和学习积极性.
例2表1是小明的中国建设银行存折的一部分,则其中数字a是

( )
A.1 501.55 B.750.69 C.500.69 D.250.69
评析该题属生活常识,背景亲切(许多学生将自己的压岁钱存入银行),主要考查学生对有理数的概念、加减法等知识的掌握以及数学应用能力.
例3《庄子·天下》有一句名言:“一尺之棰,日取其半,万世不竭”,这句话的大意是:一尺长的木棍,每天截去它的一半,千秋万代也截不完,假设庄子于公元前290年时将一根1尺长的木棍截去它的一半长,以后每过一年就截去留下木棍长度的一半,他的子子孙孙继承遗志能够不断地截取下去,直到公元2012年截取后,留下木棍的长度是______尺.
评析本题考查有理数的概念、加减法、乘方等有关知识和数学应用能力,还涉及社会生活常识,即在公元纪年的规定中,公元1年的前一年是公元前1年,没有公元0年.
2 以思想方法为指导,精选例题
中考对数学思想方法的考查是一贯的宗旨.数学思想方法存在于数学知识的学习和解决问题的过程中,因此在课堂教学所选的例题中,应特别关注渗透数学思想和方法,“顺便”地发展、提高学生分析问题和解决问题的能力,养成良好的思维习惯.
中学数学思想主要包括4类,即函数方程思想、数形结合思想、分类讨论思想和等价转化思想.
2.1 函数方程思想
例4已知商店里1瓶可乐(包括可乐汁和可乐瓶)的价格是2元,为了加强环保意识,商店规定废品必须由商店回收,且2个可乐瓶可以换得一瓶可乐.小明同学有4元钱,请问最多能喝到几瓶可乐汁?
评析不少学生没有从方程的角度思考这个问题,他只简单认为,4元钱首先能购得2瓶可乐,喝了可乐汁后可换回1瓶可乐,喝了这瓶可乐汁后,对于留下的1个可乐瓶不知道该如何处理了.本题考查的是函数方程思想.
2.2 数形结合思想
例5我们知道,二次函数的图像是抛物线,反比例函数的图像是双曲线,善于学习的小亮同学思考,这2种曲线的差异在哪儿呢?通过查阅网上资料得知:①平面内到一个定点的距离与到一条定直线的距离相等的所有点组成的图形叫抛物线;②平面内到2个定点的距离的差的绝对值等于同一个常数的所有点组成的图形叫双曲线.请分别利用抛物线和双曲线的定义解决以下问题:

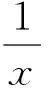
评析解析几何的核心思想是数形结合思想.该类试题可以较好地帮助学生掌握数形结合的解题方法,建立数形结合的解题思想,深刻理解“形”的关系可以通过“数”来刻画,而“数”的问题又可以借助“形”来体现.
2.3 分类讨论思想
例6已知在12个小球中有1个小球是次品(次品与正品的形状、大小和颜色都相同,只是重量不同),现给你一架天平秤,要求最多称3次,找出次品.聪明的小明将这些小球依次标上号码,第1次将①~④号小球与⑤~⑧号小球相称,结果如图2所示,因此他判定次品肯定在①~⑧号小球中;第2次将①、②、⑥号小球与③、④、⑤号小球相称,结果如图3所示;要想找到次品,第3次的称法是将______号小球与______号小球相称.

图2 图3
评析本题主要渗透分类讨论的思想,综合考查学生的思维推理能力.从第2次称的结果看,首先可以判定⑦、⑧号小球为正品,再从2次称的轻重结果看,①、②、⑤号小球也是正品,因此最后一次只要将③号小球与④号小球相称,重者为次品,若重量相同,则⑥号小球为次品,且次品稍轻.其实第1次称的结果从左端看有2种:若平,则次品在另外4个小球内,利用标准的8个小球再称2次,很容易可以找到次品;若不平,则可以视作如图2所示的结果.在接着的第2次称时,从左端的结果看有3种,分别为重(如图3所示)、平、轻:(1)若重,即为该题的结果;(2)若平,则次品为⑦号或⑧号小球,第3次只要将⑦号小球与⑧号小球相称,轻者为次品;(3)若轻,次品在①、②、⑤号小球中,最后一次将①号小球与②号小球相称:若平,则⑤号小球为次品,若不平,则重者为次品.在解决本题时所蕴含的数学思想方法、数学思维方式等是很值得回味的.
2.4 等价转化思想

图4
例7如图4,正方形OABC的边长是2,已知点O处是蚂蚁的家,在点(1,0),(2,1),(2,2),(0,2)处各有一只蚂蚁,它们正以相同的速度沿着正方形的边往前爬行.每只蚂蚁在爬行过程中,如果碰到另外一只蚂蚁,则各自掉头往回爬;如果爬到蚂蚁的家就停止爬行.那么这4只蚂蚁需要爬行的总路程的最大值是
( )
A.16 B.18 C.20 D.22
评析该题主要考查等价转化的思想,因为当2只蚂蚁各自相遇掉头往回爬时,从它们爬行的总路程看,等同于2只蚂蚁各自继续往前爬行的路程(甲替乙爬、乙替甲爬),故只要考虑每只蚂蚁爬行的最长路程即可,包含了等价代换的思想.若用分类讨论的方法来解决,则比较麻烦[2].
3 以综合能力为目标,精选例题
对学生综合能力的考核要求,也是中考的目标之一,其中包含运算能力、抽象思维能力、分析问题和解决问题能力等等较多的内容.
3.1 基本运算能力
运算能力是学生首先要掌握的基本能力,它是数学学科的重要特征.在例5中,对学生的运算能力提出了较高的要求.

图5
例8如图5,小明在比赛的一次投篮中,球的运动路线是抛物线y=ax2+3.35(a是非零常数)的一部分,当球出手的一刹那,球离地面的高度是2.725 m.
(1)求抛物线的解析式.
(2)当时小华正位于小明与篮球架之间,原地向正上方奋力跃起恰好盖帽成功.已知小华盖帽时手离地面的高度为3.125 m,求小华起跳时与小明的距离?
评析该题背景熟悉,主要考查抛物线的有关知识,涉及到学生的基本运算能力要求,同时还包含一个基本常识:“盖帽”——篮球犯规规则,即当篮球在上升过程中封盖成功为“盖帽”,而下降时的拦截不能算“盖帽”,应该算进球有效,因此本题只有一解,即离篮框近的位置是不对的,属易错之处.
3.2 合情推理能力
合情推理主要包括归纳推理和类比推理,它是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理.通俗地说,合情推理就是“合乎情理”的推理,在数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论、提供证明的思路和方向.因此在人们认识世界的过程中,合情推理扮演着很重要的角色,它是学生在后续学习和研究中创造性思维的基础和原动力.在高中《数学(选修2-2)》第2章第1节“合情推理与演绎推理”中,学生要系统地学习有关的知识.因此在义务教育阶段,培养学生的数学直觉、合情推理能力有十分重要的意义.

图6
例9在图6的数表中,第1行是由正整数按从小到大的顺序排成的,从第2行起,每一行中的数字均等于其肩上的2个数之和,例如第3行第3个数等于第2行的第3个数与第4个数之和.则第10行第2 009个数是
( )
A.11×28B.2 008×29C.2 019×28D.4 027×28
评析“观察规律找数”一直是中考的热点试题.学生要在较短的时间内解决此类问题,靠的是直觉思维,依赖的是合情推理能力.经过严密推理而“小题大做”,显然是得不偿失的.
3.3 抽象思维能力
数学是思维的学科,学生的抽象思维能力在较大程度上影响了解决数学问题的能力.

图7
例10如图7,r1,r2,r3,r4是正方形ABCD的4条对称轴.正方形ABCD关于轴r1对称得到正方形DCBA,我们把这种变换记为r1,同样把正方形关于轴r2,r3,r4对称的变换分别记为r2,r3,r4.对正方形先作变换rm,再作变换rn,记为rm·rn.善于探究的小明发现r1·r2与r3·r4的变换结果相同,可记为“r1·r2=r3·r4”,那么请你也写出一个类似的探究结果:____________.
评析该题取材于“群”的有关知识,以平面图形的“对称变换”为载体,着眼于研究“群”中运算的封闭性.试题背景熟悉,考查形式新颖,答案开放,侧重于对学生抽象思维能力的考查.
3.4 数学应用能力
随着时间的推移,学生所掌握的数学知识会慢慢遗忘,但是在学习数学知识的过程中所形成的处理问题的思想、方法、策略以及良好的思维品质、思维习惯是永久的.它将指导人们用数学的眼光来观察和思考问题,这是数学学科特有的功能.因此,教师必须有意识地培养学生的数学应用能力.

图8
例11红、绿交通变色灯的拉线开关是这样设计的:接上电源即显示红色,拉第1次开关时,灯的颜色由红色变为绿色;拉第2次时,灯的颜色由绿色变红色,拉第3次开关时;灯的颜色由红色变绿色,如此循环往复.现对编号为1,2,3,…,100的100盏交通变色灯通上电源,先将编号为2的倍数的灯线拉一下,然后将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,则3次拉完后绿色灯的盏数为
( )
A.39 B.51 C.71 D.74
评析从试题考查的数学知识角度看,该题考查了整数的有关内容;从数学思想角度看,考查了“集合”的思想;从数学素养角度看,考查了分类讨论中的“不重不漏”.图8展示的方法比较简洁:灯线拉一次就在该灯的编号上画一个圈(则画1个圈和3个圈的为绿灯),显然在1~30内有15盏,同理31~60和61~90内各有15盏,而91~100内只需数1~10内的,发现有6盏,故共有51盏绿灯.该方法充分表明学好数学能有效地帮助人们自觉或不自觉地运用数学的思想方法、思维习惯和解题策略处理具体问题.
3.5 动手实践能力
有些数学问题,学生只需要根据题意,有效利用身边的学习工具(如铅笔盒、笔和圆规等)或通过动手实践操作解决.动手实践、自主探索与合作交流是学生学习数学的重要方式.

图9
例12如图9,有3根针(标号分别是1,2,3)和套在1号针上的3张金属片.按照下列2个规则,把金属片全部移到3号针上:①每次只能移动一张金属片;②较大的金属片不能放在较小的金属片上面.你认为最少需要移动的次数是
( )
A.3 B.5 C.7 D.9
评析该题是简单的汉诺塔问题,解决它“心”动不如“行”动.学生数学知识的获得方式应该是多种多样的.在《课程标准》中提到,动手实践、自主探索与合作交流是学生学习数学的重要方式,……学生的数学学习活动应当是一个生动活泼的、自主的和富有个性的过程.
3.6 数学学习能力
学生的数学学习能力的形成主要在平时的数学学习上,尤其是数学学习的方式.完整的数学学习应包括学“问”与学“答”,完整的、有效的数学学习过程应该包括:自然、合理地提出数学问题;自然、合理地解决数学问题;自然、合理地拓展数学问题.在数学学习中,及时对知识进行归纳、类比和整理是提高学习效率的有效策略.
例13善于学习的小明在学习解一元一次不等式中,发现它与解一元一次方程有许多相似之处.小明进行了比较,如表2所示:

表2 解一元一次不等式与一元一次方程的比较
从表2可以清楚地看出,解一元一次不等式与解一元一次方程有一定的联系,它们的解题思路以及解题步骤是一致的.请仔细思考,探究下列问题:
(1)若不等式kx>b的解集是x<1,求方程kx=b的解;
(2)若方程kx=b的解是x=-1,求不等式kx>b的解集.
评析该题能让学生领会学习数学的一种策略,尽管每个学生对数学知识的学习和掌握都有自己不同的方式和方法,但有时候是可以相互借鉴的.
3.7 数学应用能力

图10
在关注核心知识的同时,还需关注近几年中考的热点问题,如应用性问题、运动型问题、实验操作、探索规律、图形变换、读图与识图、新概念问题等,它综合体现了学生的数学应用能力.新定义型试题是中考的热点之一,它可以综合考查学生的数学应用能力.
例14如图10,在梯形ABCD中,∠DAB=90°,AB∥CD,点E在边BC上,且CE=DC,BE=AB.
(1)求证:AE⊥DE.
(2)定义:如果某四边形的一条边上(除顶点外)有一个点,使得除该边2个顶点外的另外2个顶点与它的连线互相垂直,我们把满足这种条件的点叫做该四边形的“直角拐点”.例如点E在边BC上,且AE⊥DE,因此点E是梯形ABCD的直角拐点,请探究在边AD上有没有梯形ABCD的直角拐点?并说明你的理由.
(3)请判断在边CD上有没有梯形ABCD的直角拐点?并说明你的理由.
评析“直角拐点”是个新定义,对学生而言,只要不存在害怕心理,仔细阅读理解有关条件,解决它难度不大.若教师在平时的课堂教学中能有意识地渗透此类问题,则可以有效地提高学生分析问题和解决问题的能力.
在中考的系统复习中,教师应多钻研中考试题的特点,根据不同的知识、能力和思想方法的要求,精选例题.在复习课的选题中应充分关注一些适度开放和探索的问题,较多地渗透新背景的试题,使学生自己能给出对问题的理解、解答,解题后加强反思,总结经验,通过提高思维能力、增强解题直觉,从而提高对综合题的适应能力和突破能力,提高学生的解决新颖试题的适应能力,提高学生的数学素养.平时的教学要重在能力的培养上,以不变应万变,靠“题海战术”、“见多识广”、“猜题押宝”制胜的做法是行不通的!
[1] 李昌官.用积极的考试引导积极的教学——2007年台州市初中生学业考试数学命题之实践与探索[J].中学数学教学参考:初中版,2007(8):39-43.
[2] 王桂华,陈立彬.浅谈改编初中数学试题的简单方法[J].中国数学教育:初中版,2007(9):33-35.

