年年考向量 岁岁数与形——浙江省自主命题以来向量试题特点评析

●

(余杭高级中学 浙江余杭 311100)

年年考向量岁岁数与形
——浙江省自主命题以来向量试题特点评析

●曹凤山

(余杭高级中学 浙江余杭 311100)

“注重考查数学的本质、注重数学的核心思想方法考查”是浙江省数学高考试题的显著特点之一，这从试题对向量内容的考查可略见一斑.自2004年浙江省自主命题以来，每年都有一道向量内容的客观题，入口都较宽，解法多样，其中数形结合的方法往往是最优解.同时，每道试题的背后都有一个漂亮的几何背景，都对应一个浅显直观的几何结论.下面以理科试题为例，主要从数形结合的角度做简要解析.

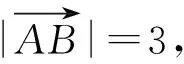
(2004年浙江省数学高考理科试题)

分析如图1，显然△ABC为直角三角形.根据向量积、向量所成角的概念，知

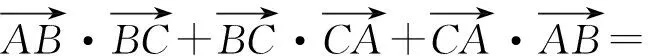
0+ac·cos(π-C)+bc·cos(π-A)=

-(a2+b2)=-c2=-25.

几何背景：直角三角形.

几何结论：直角边在斜边上射影的和等于斜边长(向量式的“射影定理”).

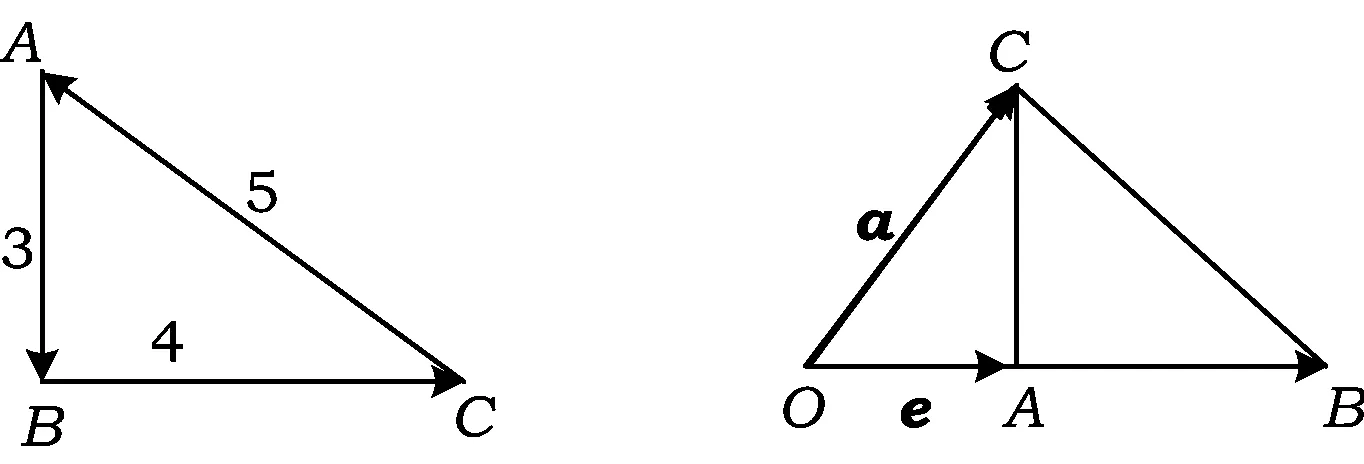
图1 图2

例2已知向量a≠e，|e|=1，对任意t∈R，恒有|a-te|≥|a-e|，则

( )

A.a⊥eB.a⊥(a-e)

C.e⊥(a-e) D. (a+e)⊥(a-e)

(2005年浙江省数学高考理科试题)

分析根据a2=|a|2进行转化是常规的思考方向.因为|a-te|≥|a-e|，即

(a-te)2≥(a-e)2，

亦即

t2-2ta·e+2a·e-1≥0,

所以

Δ=4(a·e-1)2≤0,

故a·e=1.选C.

几何背景：直线外一点到直线上点的距离.

几何结论：从直线外一点到这条直线所画的线段中垂线段最短.

例3设向量a,b,c满足a+b+c=0,(a-b)⊥c,a⊥b.若|a|=1,则|a|2+|b|2+|c|2的值是______.

(2006年浙江省数学高考理科试题)

分析如图3，由a⊥b知四边形ABCD为矩形.又因为a+b+c=0，(a-b)⊥c,所以四边形ABCD为正方形，故

c2=2|a|2，|a|2+|b|2+|c|2=4.

几何背景：正方形.

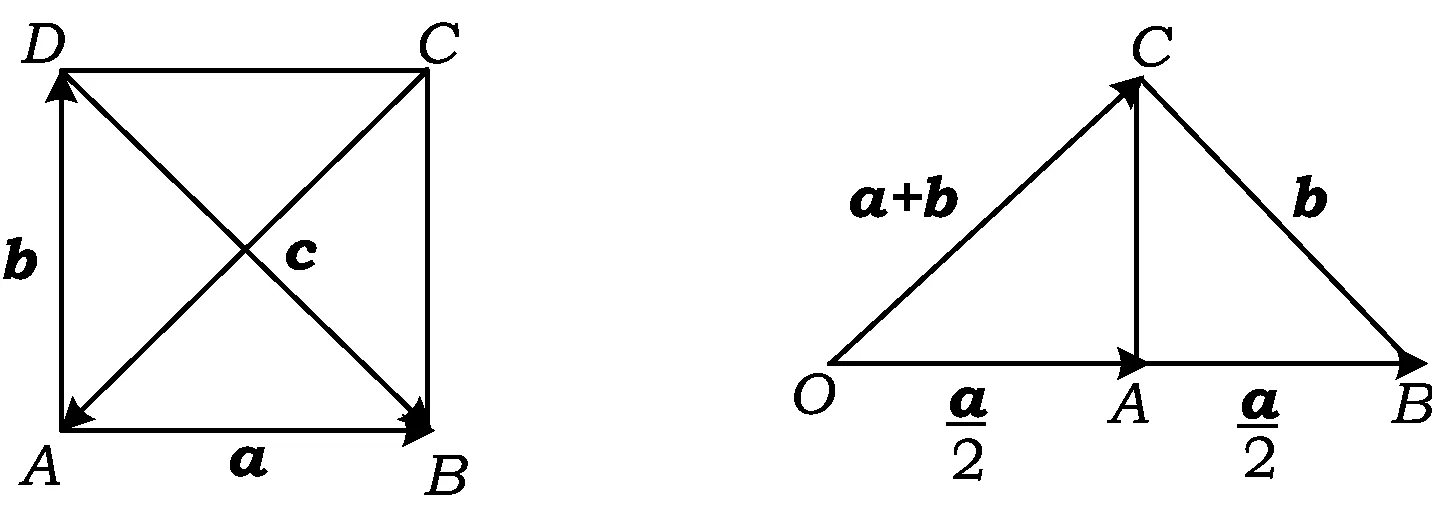
图3 图4

例4若非零向量a,b满足|a+b|=|b|，则

( )

A． |2a|>|2a+b| B．|2a|<|2a+b|

C． |2b|>|a+2b| D．|2a|<|a+2b|

(2007年浙江省数学高考理科试题)

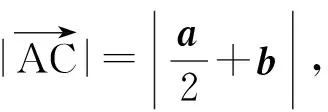
几何背景：等腰三角形(直角三角形).

几何结论：等腰三角形底边上的高小于腰(或直角三角形的直角边小于斜边，或三角形的两边之和大于第三边).

例5已知a，b是平面内2个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0,则|c|的最大值是

( )

(2008年浙江省数学高考理科试题)

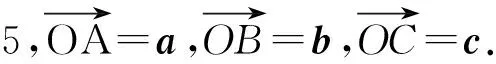
几何背景：圆.

几何结论：直径上的圆周角是直角，直径是圆中最长的弦.

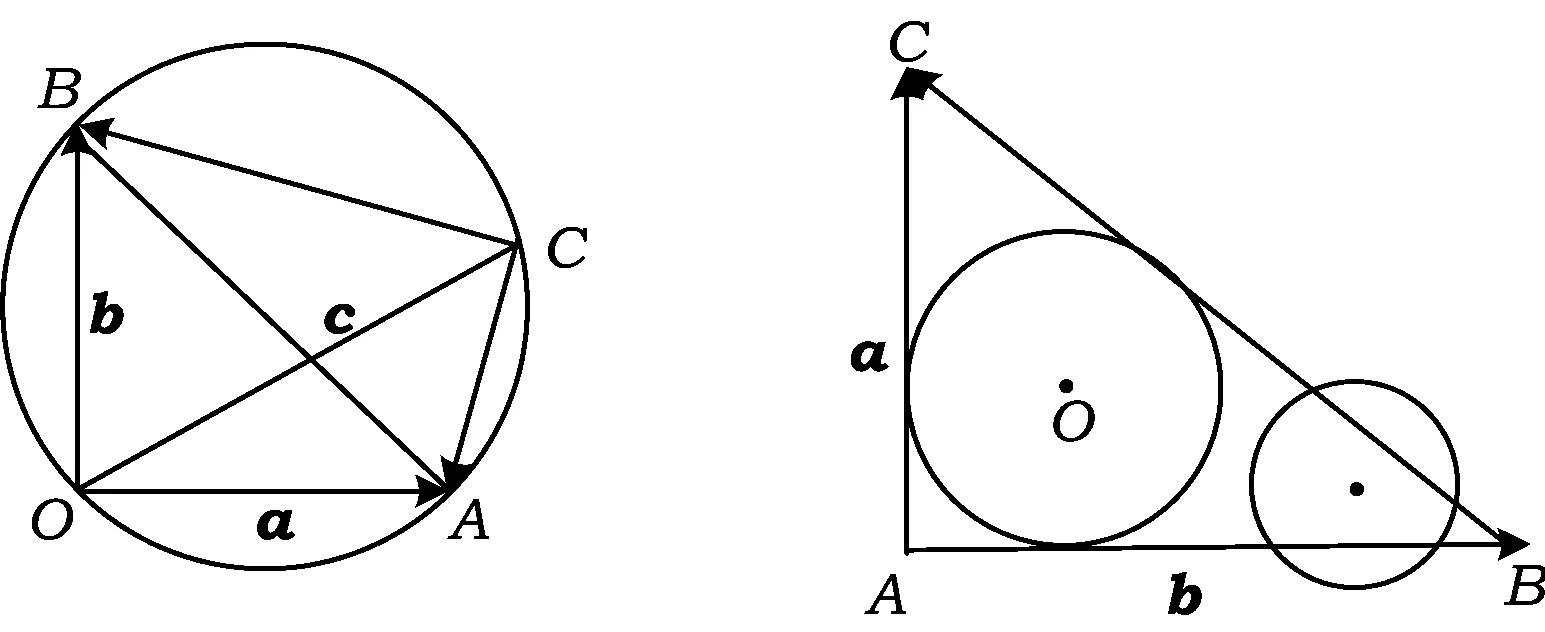
图5 图6

例6设向量a，b满足|a|=3,|b|=4,a·b=0.以a，b,a-b的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为

( )

A.3 B.4 C.5 D.6

(2009年浙江省数学高考理科试题)

分析如图6，半径为1的圆可以与三角形有4个不同的交点.下面探讨能不能有5个甚至更多的交点,也就是半径为1的圆能不能与第3条边也相交？先看一种极限的情形，圆是三角形的内切圆时，

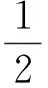
这时r=1.如果⊙O与AC有2个交点，则一定与另外2条边中的一条相离，即最多的交点个数为4个.

几何背景：(直角)三角形.

几何结论：半径等于(小于)内切圆半径的圆最多与三角形的2条边相交.

例7已知平面向量α,β(α≠0,α≠β)满足|β|=1，且α与β-α的夹角为120°，则|α|的取值范围是______.

(2010年浙江省数学高考理科试题)

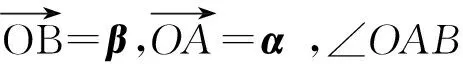
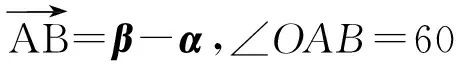
易知，点B在单位圆上，圆心为G，点A在OB所张圆周角为60°的圆的一段弧上，从而

∠OGB=2∠OAB=120°.

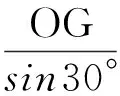
几何背景：圆.

几何结论：同弧(等弧)上的圆周角相等,同弧所对圆心角是圆周角的2倍.

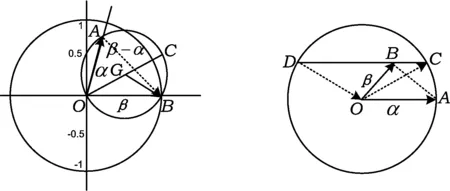
图7 图8

(2011年浙江省数学高考理科试题)

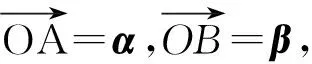
几何背景：平行四边形、三角形、圆.

几何结论：到定直线距离相等的点在一条直线上.

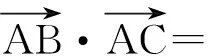
(2012年浙江省数学高考理科试题)

分析如图9，AM=3，MB=MC=5，因此

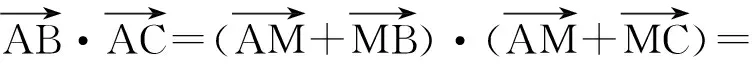
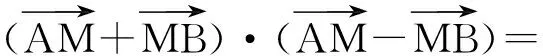
或利用

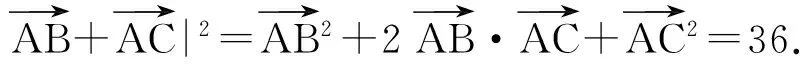
(1)

因为

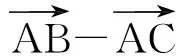
所以

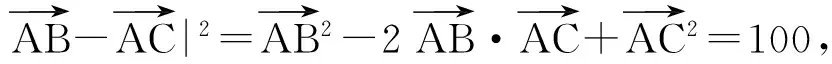
(2)

式(1)-式(2)，得

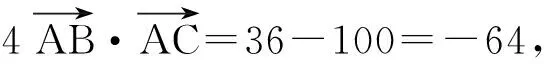
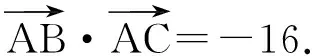
或写成

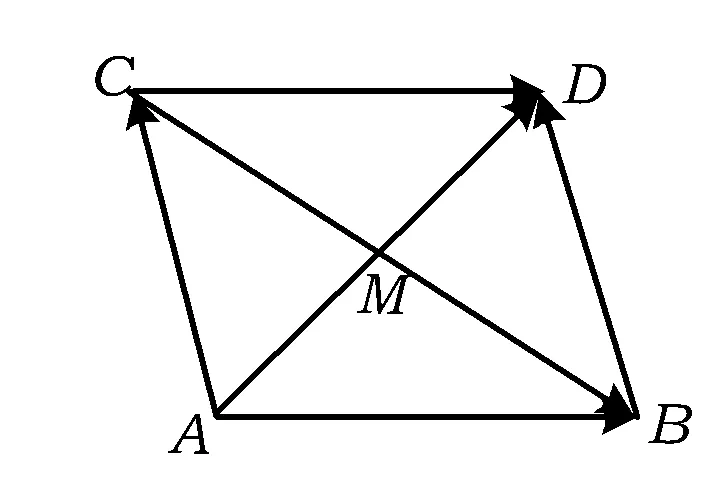
图9

几何背景：平行四边形.