析近3年高考数列考情 定2013年复习策略

●

(象山中学 浙江象山 315700)

析近3年高考数列考情定2013年复习策略

●杨冬梅邓成

(象山中学 浙江象山 315700)

浙江省数学高考对于数列的考查飘忽不定，高考复习很难把握，接下来由笔者一一为您解密，以此揭开2013年高考数列复习的神秘面纱.

1 浙江省数学高考数列考查要求

高考数列重点考2条主线：一条是数列的数列特征：理解等差、等比数列的概念，掌握等差、等比数列的通项公式与前n项和公式，利用等差、等比数列前n项和公式及其性质求一些特殊数列的和.一条是数列的函数特征：等差数列与一次函数、等比数列与指数函数的关系.

2 近3年浙江省高考文、理科数列考查情况

命题特点文科解答题每年必出一题，选择题、填空题不确定，分值在14～23分之间;理科只有2011年考了解答题，其余3年只考小题，分值在4～14分之间.

知识层面纵观近3年浙江省数学高考，数列试题主要考查等差、等比数列的定义、通项、求和等基础知识，出现频率最高的知识点是等差、等比的通项与求和，同时结合不等式、二项式定理(理科)等基础知识综合考查.

能力层面近3年浙江省普通高中考试说明中强调“以能力立意”，即以数列的相关知识作为载体，从数列问题入手，侧重体现对数列知识的理解和应用，尤其是综合应用和灵活应用．个性品质要求关注思想价值立意，注重通性通法，淡化特殊技巧，注重等差(等比)数列的概念、本质和解决数列问题的常规方法，具体表现为试题的情境熟、入口宽、有层次，有利于学生在公平的背景下展示真实水平，体现考生个体的情感、态度和价值观，表现出考生的思维习惯是否慎密等．

浙江省考题与全国卷、其他省市卷数列题有区别，浙江省对数列的考查主要着眼于数列的基础知识与基本方法，作为中档题，回避了递推数列和复杂的不等关系的论证，主要揭示等差和等比数列内在的本质性知识，形成浙江卷数列题的特色．

3 近3年全国各地高考文、理科数列考查情况

笔者翻阅了近3年18个省市的高考文、理科105份数学试卷，发现数列部分的考查具有如下特点：

命题特点大部分省市会出现1～2道与数列有关的试题，个别省市会出项3道数列试题.以2012年数学高考为例，福建、辽宁、四川理科卷考查了3道，湖北、江西和大纲全国文科卷考查了3道.有的省市文科考1道、理科考2道，而有的省市却正好相反，而大多数省是文、理科各考2道与数列有关的试题.以解答题的形式考查为各省市的重点，理科相对较难.

知识层面主要考查等差、等比数列的定义、通项、求和等基础知识，注重通性通法，淡化特殊技巧.出现频率最高的知识点是等差、等比的通项与求和；与其他知识的交汇命题是高考的难点，其中与不等式的交汇试题中考放缩法的试题较难.上海市引领高考数列的新潮，常考创新题.

能力层面主要考查运算求解能力、推理论证能力、分析问题和解决问题的能力、创新思维能力等.

数学思想主要考查函数与方程的思想、化归与转化思想、分类讨论思想、递推思想等.

4 亮点扫描

4.1 重视基本概念、基本运算，注重通性通法

纵观高考卷，对等差(等比)数列的定义、通项公式、求和公式等基本概念、基本运算的考查，依旧是这3年数学高考“数列热点”中的重点，题型分布极为广泛，一般表现在客观题或主观题的第(1)小题，其难度不大，平时应注重通性通法.

例1设公比为q(q>0)的等比数列{an}的前n项和为Sn．若S2=3a2+2，S4=3a4+2，则q=______.

(2012年浙江省数学高考理科试题)

分析简解运用基本量法转化为a1,q的方程，解方程组即可.

点评类似的题目很多，这些都是基础题，题号靠前，只要合理地运用定义、公式进行仔细计算即可解决此类问题.

4.2 重视等差数列、等比数列的函数特征

等差数列的通项与一次函数、前n项和与二次函数、等比数列与指数函数的关系是数列的函数特征的体现，数列具有函数的很多性质，如单调性、对称性、周期性、最值等，如果从函数的角度思考问题，很多问题就迎刃而解了.

例2设Sn是公差为d(d≠0)的无穷等差数列{an}的前n项和，则下列命题错误的是

( )

A．若d<0，则数列{Sn}有最大项

B．若数列{Sn}有最大项，则d<0

C．若数列{Sn}是递增数列，则对任意的n∈N*，均有Sn>0

D．若对任意的n∈N*，均有Sn>0，则数列{Sn}是递增数列

(2012年浙江省数学高考理科试题)

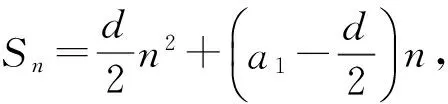
点评数列的函数特征是数列的重要特征，要重点关注.如2011年浙江理科第17题也考查数列的函数性质.

4.3 文科常规背景呈现，考查基础知识

文科对数列的考查要求比较低，以常规背景呈现，常见的题型有：基本运算题、推理论证题等.试题位置相对靠前，考查基础知识，是命题者在设计中认为考生应该得分的题目，在平时的教学中应加强解题规范和正确率的培养.

例3已知数列{an}的前n项和为Sn，且Sn=2n2+n，n∈N*，数列{bn}满足an=4log2bn+3,n∈N*.

(1)求an,bn；

(2)求数列{anbn}的前n项和Tn.

(2012年浙江省数学高考文科试题)

分析(1)an=4n-1，bn=2n-1,n∈N*.

(2)由第(1)小题知

anbn=(4n-1)·2n-1,

从而

Tn=3+7×2+11×22+…+(4n-1)·2n-1,

2Tn=3×2+7×22+11×23+…+(4n-1)·2n,

于是

2Tn-Tn= (4n-1)·2n-[3+4(2+22+…+2n-1)=

(4n-5)2n+5,

故

Tn=(4n-5)2n+5.

4.4 理科交汇整合呈现，综合应用把关

数列与数学归纳法、二项式定理、概率、解析几何、不等式的交汇等，其中与不等式的交汇试题是浙江省考查的一大亮点,考查考生综合应用能力.

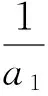
(1)求数列{an}的通项公式及Sn;

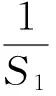
(2011年浙江省数学高考理科试题)

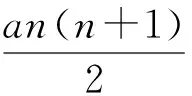
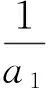
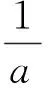
当n≥2时，

即

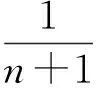
因此，当a>0时，AnBn.

点评本题的最大亮点是题目简洁、表达朴素、内涵丰富．主要考查了等差与等比数列的概念、通项公式、前n项和公式，也考查了其他数列(能裂项相消)的前n项和，结合不等式的知识考查了二项式定理、数学归纳法等内容．

5 复习策略

分析近3年高考数列的考查情况，不难揭开2013年数列复习的神秘面纱，在数列复习过程中只要抓住下面的几点就能迎刃而解了.

(1)吃透1个定义即数列的定义.

(2)突出2条主线数列特征,即等差、等比数列的有关性质与函数特征：即单调性、对称性、周期性、最值等.

(3)活用3类方法:基本量法:a1,an,n,Sn,d(q)知三求二;求通项方法：公式法(考查最多)、累加法、累乘法、待定系数法等；求和的方法：公式法(考查最多)、错位相减法、裂项相消法、分奇偶讨论法、绝对值数求和.

(4)关注4大题型.

基本运算题.通常涉及等差数列、等比数列的通项公式，前n项和公式，常常运用基本量法解决(80%左右).

推理论证题.如证明问题:证明恒等式(考查过3次)；证明不等式(考查过9次)；证明等差、等比数列(考查过11次)等.

知识交汇题.数列与其他主干知识交汇的考题正在增多，常见的交汇有：数列与函数(考查过6次)、数列与导数(考查过7次)、数列与三角(考查过5次)、数列与二项式定理(考查过2次)、数列与概率、数列与解析几何(考查过3次)、数列与不等式的交汇(考查15次).

情境创新题.一种是引入新概念、定义新数列的一类试题．另一种是以数列知识为背景的实际应用问题.

(5)领悟5大思想考试说明指出对数.

数学思想方法的考查是对数学知识在更高层次上的抽象和概括的考查，通过对数列知识的考查，反映考生对数学思想方法的掌握程度.

函数思想.即数列的函数特征(考查过12次).

方程思想.基本量法是解决数列问题的最基本的方法，经常结合数列通项公式和求和公式构建方程或方程组求解，因此方程思想非常重要.

分类讨论.数列中渗透分类讨论的思想．例如由Sn求an，要分n=1和n≠1进行讨论;在数列求和中有时需要进行奇偶讨论;有些数列的通项公式是分段表示的，解题过程需要讨论等.

化归与转化.非等差、等比数列的问题常通过构造转化为等差或等比数列求解;将一般的数列问题转化成等差或等比数列问题，是化归转化的重要目标．

递推思想.递推是数列的本质性内涵，虽然递推数列不是浙江省高考涉及的内容，但是递推思想和方法在解决数列问题中的作用是很大的．涉及数列前n项和的关系问题，常采用递推思想来解决．

与其他省市的数列试题相对比，浙江省数学高考的数列题难度中等．纵观各省市考情，关于数列的教材内容有差异，考试要求有所不同，考查的风格也各有特色．但总体来说，等差、等比数列是永恒的背景，基本量运算是不变的旋律，与其他知识的结合是发展的方向，有关的应用问题则是创新的源泉．