峰高方显谷深 一山自有一景——2013年浙江省数学高考理科卷第18题阅卷体会

●

(金华市第一中学 浙江金华 321015)

峰高方显谷深一山自有一景——2013年浙江省数学高考理科卷第18题阅卷体会

●金建军

(金华市第一中学 浙江金华 321015)

2013年高考已落下帷幕，社会各界对浙江省数学高考试题的评价众说纷纭.笔者的总体感受是“变化不大、稳定持重，经典频现、适度创新”.试题在命题立意、试题结构、材料选取、语言表述、知识点考查等方面都呈现了这一特点.笔者有幸参加了2013年数学高考阅卷工作,下面就理科卷第18题进行评析，谈一些体会与思考,与读者共飨.

例1在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.

(1)求d,an；

(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.

(2013年浙江省数学高考理科试题)

1 卷土重来未可知——意外

自2009年浙江省开始实行新课标高考以来,至今已5年.其中前3年理科卷解答大题一般都是三角函数、概率期望、立体几何、解析几何、函数与导数五大主干知识，2011年则以数列大题替换了概率题，2012年又重复原有情况，2013年是继2012年数列题“退出江湖”后再次“卷土重来”,实为意料之外，情理之中.表现为:

师生普遍认为2013年仍将是以数列代替概率且以大题形式出现,结果理科试卷中三角函数不作为单独的解答题考查，从而造成这些意外.这说明浙江高考稳中有变,启示我们平时要扎实地做好每个知识点复习，而不是猜测高考考什么.其实,高考对三角、数列、概率的考查通常归入容易题的范畴,以小题(主观题)的形式考查居多，这种轮转有助于保证主干知识的核心地位和重点考查，也在情理之中.

2 众里寻她千百度——探源

本题背景叙述简洁，具有高考试题概念清晰、思维深刻、解法多样等特点，“入手容易深入难”，由“知识立意”转化为“能力立意”，意蕴深邃，平淡之中显新意.试题源于课本,活于教材,命题常规.这些试题对学生来说具有“亲切感”，对教学有积极的导向作用：引导教师在高三复习教学中重视教材、研究教材，不搞“题海”.与之相似的平时常规练习题例举如下：

例2已知数列{an}，满足an=|32-5n|，求此数列前n项的和Sn．

变式已知数列{an}的前n项和Sn=10n-n2，又bn=|an|，求{bn}的前n项和Tn.

(2003年浙江省数学会考试题)

然而阅卷后却让我们痛惜不已:考生答题不甚理想,与命题者的期望值有一定距离.那么,这道试题有哪些特点?考生解答时有哪些典型错误?产生这些错解的根源在哪里?针对以上这些,有哪些备考建议?

3 他山之石可攻玉——借鉴

3.1 命题意图

本题紧扣高考考试说明，考查等差数列、等比数列的概念，等差数列通项公式、求和公式等基础知识，同时考查运算求解能力.

3.2 解法分析

浙江省考试院提供的参考答案为：

解法1(1)由题意知5a3·a1=(2a2+2)2，

即

d2-3d-4=0，

故d=-1或d=4，从而

an=-n+11或an=4n+6(n∈N*).

(2)设数列{an}的前n项和为Sn．因为d<0，由第(1)小题得d=-1，an=-n+11，所以

①当n≤11时，an≥0,从而

②当n≥12时，an≤0,从而

|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=

综上所述，|a1|+|a2|+|a3|+…+|an|=

该解题有一个关键点:a1,2a2+2,5a3成等比数列,如何列式代入化简；一个难点:如何对|an|去绝对值进行分类讨论.

学生的普遍解法如下：

解法2(1)略.

(2)由第(1)小题知,当d<0时,an=11-n.

①当1≤n≤11时,an≥0,从而

|a1|+ |a2|+|a3|+…+|an|=

②当n≥12时,an≤0,从而

|a1|+|a2|+|a3|+…+|an|=

a1+a2+a3+…+a11-(a12+a13+…+an)=

2(a1+a2+a3+…+a11)-(a1+a2+a3+…+an)=

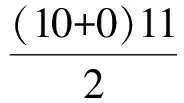
在阅卷中第(1)小题关于d的方程形式有：

①5(a1+2d)·a1=(2a1+2d+2)2；

③484+88d+4d2=500+100d；

④4d2-12d-16=0．

第(2)小题分类讨论的形式有：

①分为1≤n≤11(n<12)和n≥12；

②分为1≤n≤10和n≥11等.

当n≥12时，Sn的可能形式有：

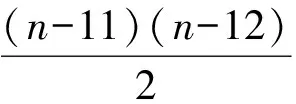
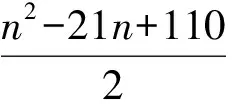
这些都作为正确结论，体现人文关怀.

4 山重水复疑无路——析误

4.1 难度值

本题平均得分为9.8左右，难度系数在0.7左右.

4.2 主要错误

学生出现的主要错误有以下几种情况：

对于第(1)小题：

①概念错误：对于3项成等比数列，学生不知道如何表示或表示错误，少数学生本题得分为0；

②公式记错：如当an=a1+(n-1)d写成an=a1+n(n-1)d；

③化简错误：不能将式子化为d2-3d-4=0，有些学生解方程有误，解为d=1或d=-4；

④书写错误：如d=-1时将an=a1+(n-1)d=11-n写成9-n.

对于第(2)小题：

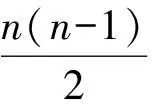
5 柳暗花明又一村——启示

从阅卷情况看，学生基础知识、基本技能的掌握情况不容乐观.主要表现为：概念模糊、公式记错；考虑不周、计算出错；复杂运算不能转化；分类不明，常规问题准确性低，基本的解题书写规范亟待改进.考试反馈表明，加强“双基”教学是高考获取成功的根本要素，教学时务必引起重视.教学时要认真钻研考试说明，不搞怪题偏题，使学生在不同的情境下巩固双基，提高综合解题能力.

教学中要关注反思和拓展，品味解题的方法和关键，探究一题多解，一题多变，深入理解数学本质.因此数学思想和本质的揭示要时时渗透在日常教学中.如在等差数列、等比数列通项公式的推导过程中要注意引导学生揭示和提炼用“累加法”和“叠乘法”求通项的一种思想方法；在等差数列、等比数列的前n项和公式的推导中则要求学生概括和领悟出“倒序相加法”和“错位相减法”的精髓.这些被概括和提炼的数学思想方法源于课本，都是反映数学本质的东西.

总之，2013年浙江省数学高考试卷体现了新课标下的高考要求，传递了一个信息：高中数学教学应重视概念，回归教材，克服“轻概念、重训练”的现象，着力培养学生的思维能力，实现教学的自然回归，引导中学数学教学从“题型+技巧+训练”走向“概念+构建+思维”.