蜂窝板结构等效弹性模量的测试
郝鸿雁,黄志亮
(1.浙江海洋学院机电工程学院,浙江 舟山 316000;2.三一集团有限公司研究总院,湖南 长沙 410100)
0 引 言
由于蜂窝板具有重量轻、强度高、刚性大、稳定性好、隔热隔声等优点,现已广泛应用在航空航天、机车、船舶、汽车和建筑等领域[1-3]。蜂窝板结构的静、动力学分析计算成为现阶段力学领域研究的一大热点。以往的研究大多数采用数值解析法进行分析,但其不适用于复杂的蜂窝板结构,利用ANSYS等通用有限元软件对蜂窝板结构进行力学分析时,由于没有蜂窝结构单元,使得计算只能采用等效的方式进行。蜂窝板的等效参数可以通过理论方法[4]或实验方法确定。
理论方法确定等效弹性模量计算过程比较复杂,文献[5]采用三点弯曲线载荷两端简支板的挠度测试方法,得到蜂窝板的等效弹性模量。这种方法后续的计算过程相当繁琐,并且它是一种静态的方法。本文提出利用动力学的方法来测试蜂窝板的等效弹性模量的新方法。采用LMS Test.lab声振试验系统对某型蜂窝板结构样件进行模态试验,获取了结构的固有频率和振型。用ANSYS Workbench有限元软件对试验结果进行调参,寻求结构的等效弹性模量。
1 蜂窝板结构样件模态试验
试验模态分析是一种系统辨识的方法,是在满足实际结构可以运用“模态模型”来描述其动态特性的条件下,通过对振动响应数据的处理和分析,寻求其模态参数,包括频率、阻尼和模态振型[6]。
实际工程中,需根据实验目的选择不同的模态参数估计方法。多参考点最小二乘复频域法(PolyMAX)是比利时LMS公司开发的一种全新的模态参数频域识别方法[7]。PolyMAX法既适用于弱阻尼也适用于强阻尼密集模态系统,即便是未得到充分激励的模态也能良好的识别出来。
PolyMAX法是以频响函数矩阵H作为拟合函数,H的频域矩阵分式表达为
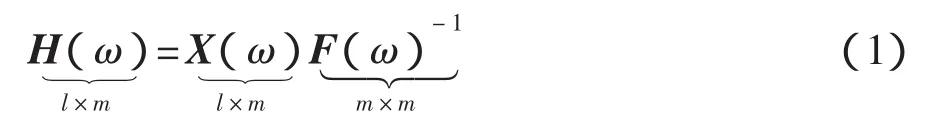
式中:m——输入(激励)参考通道总数;
l——输出(响应)通道总数。
将分子、分母定义成多项式的形式为
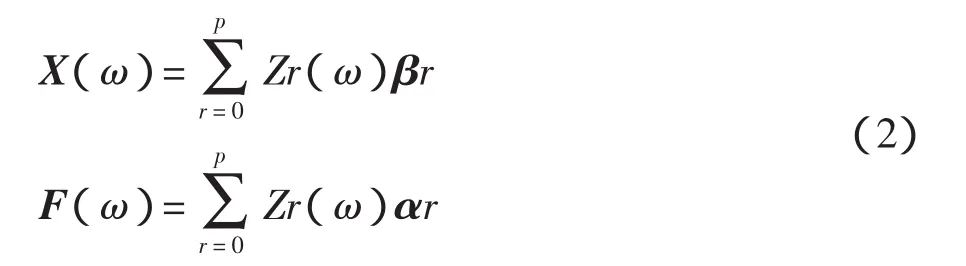
式中:Zr(ω)——多项式基本项,表达式为=e-jωΔt;
βr——l×m阶分子多项式系数矩阵;
αr——m×m阶分母多项式系数矩阵;
p——数学模型设定的阶次;
Δt——采样时间。
将式(2)代入式(1)得到的频响函数矩阵为
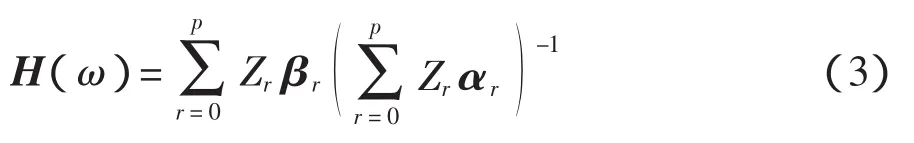
在PolyMAX法中一般设定αr、βr中的元素均为实值系数,于是可表示为

对于频响函数FRF数据频率轴上任意频率ωk,由实测频响函数可以列出式(3),取不同的频率列出足够数量的方程。最后利用最小二乘法估计便可求得待定的分子和分母多项式系数矩阵βr、αr(r=0,1,…,p),通常取 αp=Ⅰ。
在求得分母多项式系数矩阵αr的基础上,将其扩展成友矩阵的形式;再对友矩阵进行特征值分解,就能得出系统的极点和模态参与因子
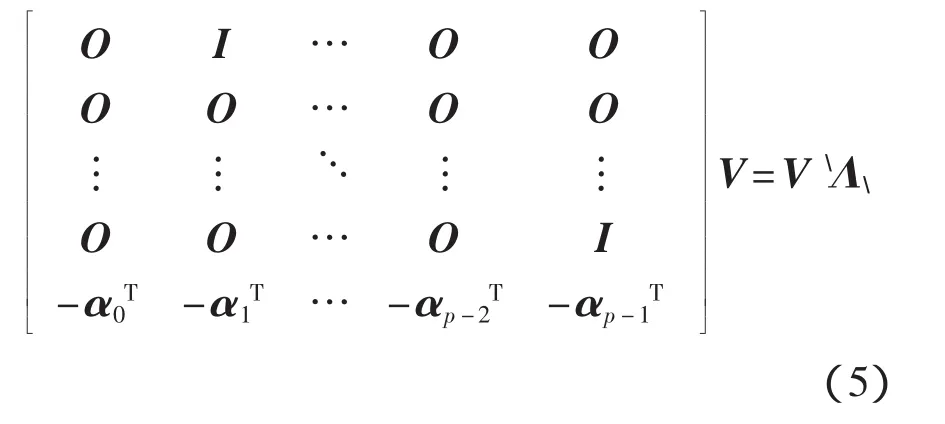
其中,Λ为友矩阵的特征值矩阵(对角阵),其对角线元素(特征值)为λi=e-piΔt(i=1,2,…,mp),它们总是以共轭复数形式成对出现的,且

由特征值分解得到的特征向量 V(mp×mp),取其最下面m行构成的矩阵即为模态参与因子矩阵L(m×mp);其每一列向量li代表各个输入对相应模态的比例贡献。
PolyMAX法采用一种比较简便的方法,即采用最小二乘频域法(LSFD)求模态振型,其拟合函数为
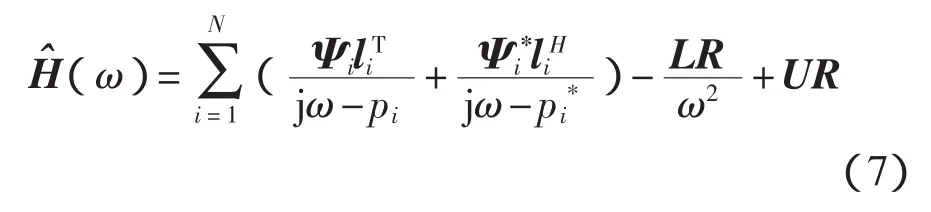
Ψi(l×1)——待求的第i阶模态振型列向量;
liT(1×m)——模态参与因子行向量;
liH(1×m)——li的共轭转置;
LR、UR(l×m)——分析频带有外模态影响的下残余项和上残余项。
由于极点pi和模态参与因子向量都已求得,于是可由测量的频响函数(ω)按不同频率列出式(7),然后用线性最小二乘法求出式中未知的模态振型Ψi以及上、下残余项LR、UR。
1.1 模态试验方法及其测试系统
本实验利用多点激励单点拾振的方法对蜂窝板在自由约束状态下进行模态试验分析。实验使用300mm×300mm×3mm、345g的蜂窝板样件,总计布置了36个测点,试验模型及测点布置如图1所示。实验中将蜂窝板4个角用软海绵垫支撑以模拟其自由约束状态。
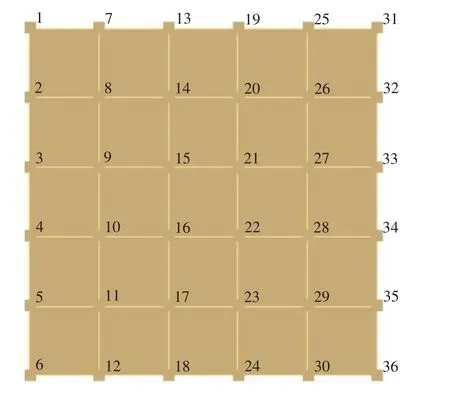
图1 蜂窝板试验样件几何测点布置
在LMS Test.lab声振试验系统中,利用锤击法对蜂窝板试验样件进行了实验模态分析。模态试验测试系统框图见图2。
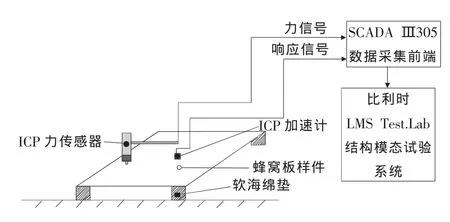
图2 基于LMS Test.lab蜂窝板结构模态试验系统框图
模态试验时,将一个PCB 333B30单向加速度传感器(质量约为4g)固定于10#测点,移动脉冲锤依次进行频响函数的测量。根据板壳振动理论[8]可知,其相对质量ζ近似等于零;因此,附加传感器的质量对模态试验结果的影响可以忽略不计。

式中:m——附加质量;
M——板的质量。
1.2 模态试验结果
采用PolyMAX模态参数识别法[7]对频响函数从100~400Hz进行模态分析,得到的稳定性分析图如图3所示。
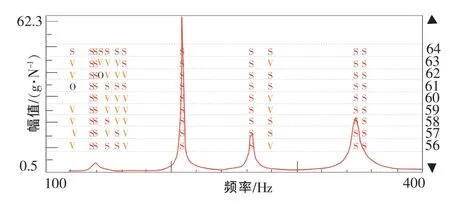
图3 PolyMAX法模态稳定性图
从图3中可以看出:有模态的位置出现一系列s标识,这说明利用PolyMAX法分析得到的频率、阻尼和模态参与因子全部稳定。
采用PolyMAX法识别出来的蜂窝板样件模态参数见表1。自由约束状态下的模态振型如图4所示。
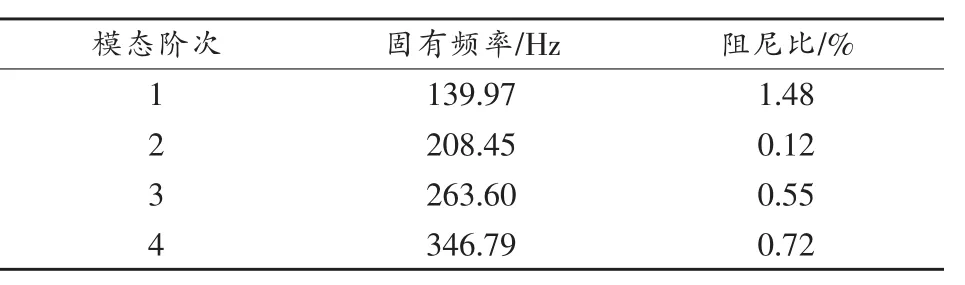
表1 自由约束状态下蜂窝板试验样件模态试验结果
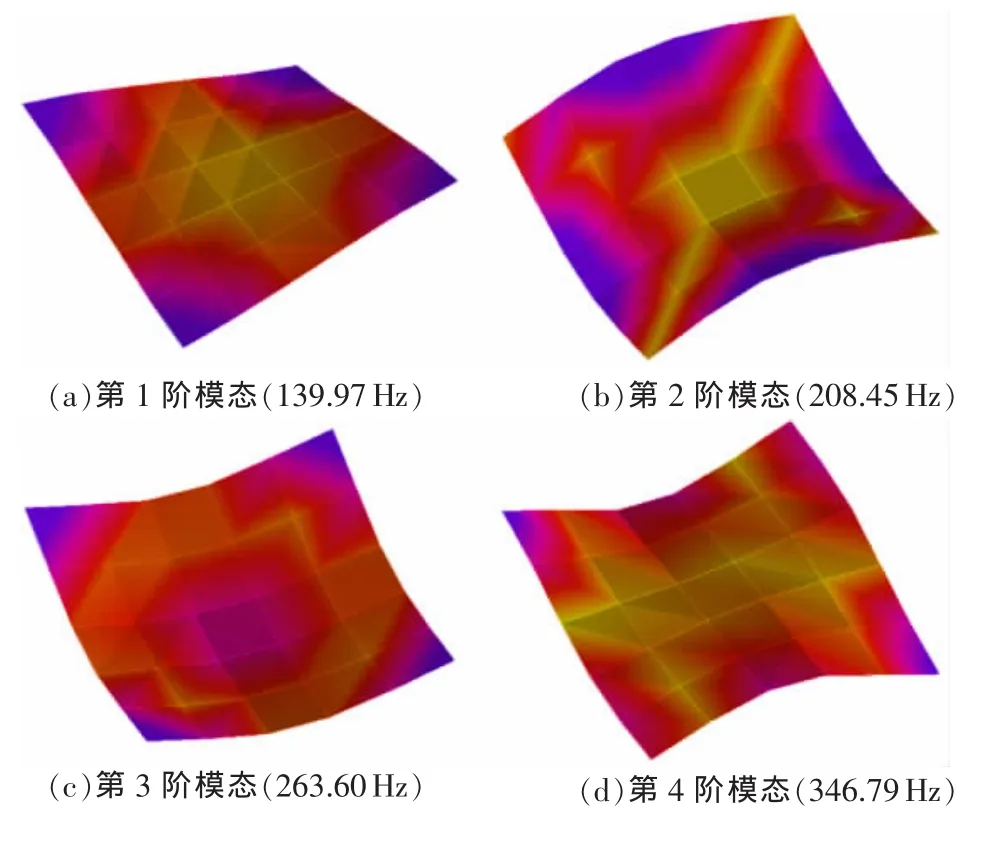
图4 蜂窝板试验样件前4阶模态振型
模态试验完成后,为防止引入虚假模态和丢失真实模态,需要对模态进行验证。而模态判定准则(modal assurance criteria,MAC)不仅可以检验模态的真实性,更广义地说它是衡量模态有效性的尺度。其中模态判定准则通过比较不同模态向量间的线性相关性来判断各阶模态的置信度。在工程分析中,两个模态振型向量Ψi和Ψs之间的模态判定准则定义为
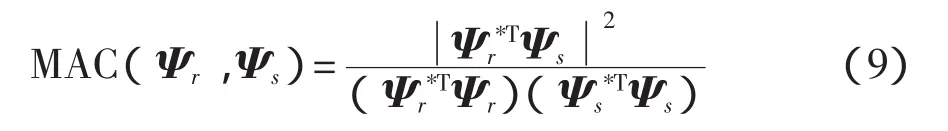
MAC取值从0到100%。若MAC取值越接近100%,则两个模态振型向量是同一个物理振型的估计;若两个模态振型向量是不同物理振型的估计,则MAC取值应该接近0。即取值为100%说明两者是同一物理振型且具有一致的相关性,同时也说明了模态参与因子的有效性;反之,若MAC取值为0,则说明两个模态振型向量是不同的物理振型且没有一致的相关关系,它们是相互独立的。
从模态置信分析图5中可以看出,由PolyMAX模态参数识别法识别出的蜂窝板各阶模态之间满足模态正交性原理;同一物理振型具有比较好的一致性,不同物理振型基本上是相互独立的。因此,本次模态试验所得到的蜂窝板结构模态真实可靠,不存在虚假模态。
2 蜂窝板等效弹性模量的确定
2.1 蜂窝板的等效方法
本文试验的蜂窝板是在假定空间体积和厚度不变的情况下,将其等效成一个等厚度的实心板。等效实心板的密度就可以由蜂窝板试验样件的重量除以实心板的体积得到。
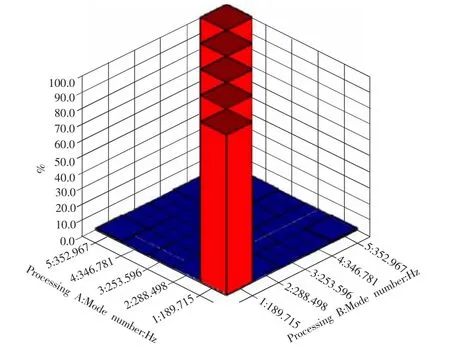
图5 蜂窝板结构模态置信分析图

式中:M——板的质量;
V——板的空间体积。
通过计算蜂窝板等效密度ρ=1278.11kg/m3。
2.2 基于ANSYS Workbench调参确定等效弹性模量
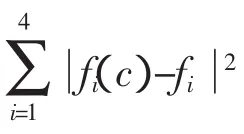
经过多次调参试凑,使有限元分析得到的固有频率和振型与实验结果趋于一致,从而得到蜂窝板等效模型弹性模量的确定值E=55GPa。
在等效弹性模量E=55GPa的情况下,蜂窝板等效模型结构模态有限元分析结果见表2,前4阶模态振型如图6所示。
通过对比蜂窝板等效模型模态有限元分析结果与实验结果可以看出,各阶模态振型非常一致,模态振型分别为:第1阶模态为对边节线四角局部振动,第2阶模态为对角节线四边局部振动,第3阶模态为环形节线局部振动,第4阶模态为对边1节线和对边2节线局部振动;且各阶模态振型对应固有频率非常接近,误差在5%以内。说明通过试验调参得到的蜂窝板结构的等效弹性模量,在动力学仿真分析中能够准确反映蜂窝板实际结构的动态特性。
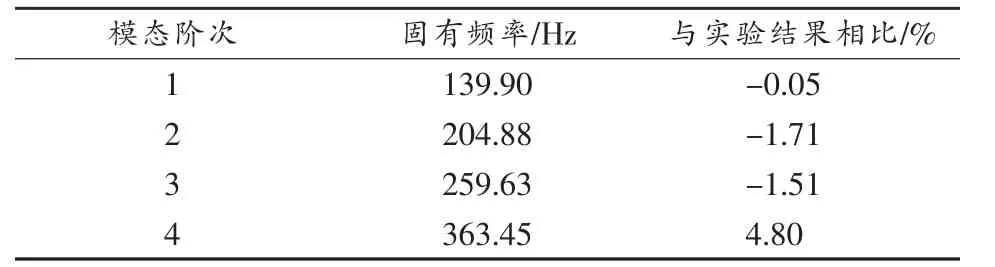
表2 自由约束状态下蜂窝板等效模型模态有限元分析结果
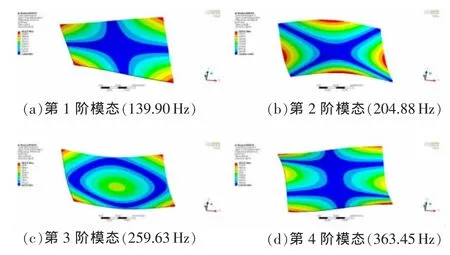
图6 蜂窝板等效模型前4阶模态振型
3 结束语
本文所采用的蜂窝板等效模型以及调参确定的等效弹性模量,在动力学分析时能够真实反映蜂窝板实际结构的动态特性。在等厚度等效方法的情况下,所确定的等效弹性模量真实可靠。同时该等效模型及其等效弹性模量也适用于静力的有限元分析。
[1]彭明军,孙勇,沈黎,等.面板对钎焊蜂窝铝板平压性能的影响[J].材料导报,2006,20(7):471-472.
[2]迎春.镁合金蜂窝板的制备及力学性能研究[D].大连:大连交通大学,2009.
[3]付立英,王维扬.卫星用蜂窝夹层板的等效计算及实验研究[J].科学技术与工程,2008,8(27):6429-6432.
[4]陈昌亚,王德禹,王本利.动力学分析中铝蜂窝夹层板的等效问题[J].空间科学学报,2002,22(增刊 2):142-148.
[5]程军,曾伟明,方如华,等.金属蜂窝夹芯板等效弹性模量的实验测试[J].实验力学,2003,18(1):50-55.
[6]Ward H,Stefan L,Paul S.Modal analysis theory and testing[M].Leuven Belgium Department of Mechanical Engineering,Katholieke Universiteit,1995:80-99.
[7]刘馥清,安宏伟.多参考最小二乘复频域(PolyMax)法在汽车轮胎及车身模态参数识别中的应用 [C]∥2006LMS首届用户大会论文集.苏州:2006:1-7.
[8]曹志远.板壳振动理论[M].北京:中国铁道出版社,1983:59-67.

