基于Copula函数的部件相关串联机械系统可靠性分析
刘 喆,陶凤和,贾长治
(军械工程学院,河北 石家庄 050003)
0 引 言
武器装备是作为一个整体系统在战场上使用的,需要经常考虑它整体系统的可靠性指标。由于实验条件的限制,只能假设装备各个构件是相互独立的,从而对这些构件单独进行试验,根据独立性假设计算获得系统的可靠性。
在装备的实际使用过程中,周围的环境因素、使用工况等同时作用于装备整体,这必将造成零部件的可靠性有共同的发展趋势,即各部件有着一定的相关性,此时仍采用独立性假设是不合适的;因此,如何根据装备各构件独立的可靠性试验数据得出具有相关性的串联机械系统的可靠性,是本文研究的目的。
在现代的可靠性研究中,一种常用手段是随机模拟的方法,然而该方法对算法、建模精度、模拟次数等要求较高,同时由于抽样方法的不同,有可能导致偏差较大。随机向量的联合分布函数是刻画随机向量概率性质的重要工具之一,它包含了两方面的信息:一是变量的边缘分布信息,另一个是变量间相关结构的信息。边缘分布信息相对容易获得,即对部件单独进行试验可以得到部件的边缘分布,但是变量间相关结构的信息很难获取。如果能够在联合分布函数中除去边缘分布的信息,那么就仅剩下了相关结构的信息。同时,如果引入Copula函数来构造多元随机变量的联合分布函数,将有利于解决相关部件的系统可靠度求解的问题。
1 Copula函数的定义和基本性质
1959年Sklar[1]最早提出Copula的概念:Copula是由一维随机变量的概率积分变换引入的。对于一维的连续型随机变量x,如其有分布函数F(x),由概率积分变换得到的 F(x)是服从[0,1]上的均匀分布,则一个二维Copula是满足以下条件的一个函数:
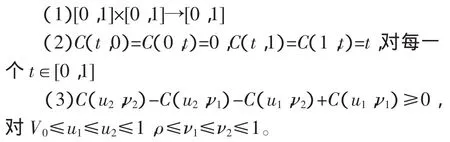
Sklar通过定理[2]说明,若X、Y是具有联合分布函数H(x,y)的随机变量且边缘分布函数分别是F(x),G(y),则对所有的 x、y存在唯一的与之对应的Copula 使:H(x,y)=C(F(x),G(y))。Copula 将 X、Y的联合分布函数H(x,y)与其边缘分布函数联系起来,展现了联合分布函数由它们的边缘分布函数生成的变化特性。许多实际应用中经常关心随机变量的寿命问题,如在可靠性理论中讨论了串联系统的寿命,而且为了方便引入了可靠度函数R(x)=P(X≥x)==1-F(x),对于具有联合分布函数 H(x,y)的二维随机变量(X,Y)也有可靠度函数R(x,y)=P(X≥x,Y≥y),Nelsen 等人提出与之对应的生存Copula——(u,ν)=u+ν-1+C(1-u,1-ν),C(1-u,1-ν)表示 P(X≥x,Y≥y)。
研究两个随机变量的相依性是Copula的一个重要应用,l966年Lehmann引出了正相依和负相依的概念[3]。设X1,…,Xn是具有联合分布函数H(x1,…,xn)的随机变量,且分别有连续的边缘分布F1,…,Fn以及 Copula,若对所有的 Rn中的(x1,…,xn),有 H(x1,…,xn)≥F(x1)F(x2)…F(xn),则 X1,X2,…,Xn是正相依的,简记为 PDQ(X,Y)。
在可靠性理论中,对系统寿命的研究只限于各个部件独立的情况,在本文中将讨论部件之间不相互独立的时候系统的可靠度,把系统寿命的问题和Copula函数联系了起来,通过Copula的性质来探讨系统寿命的一些变化[4]。
2 部件相依的串联系统可靠性分析
机械系统中,可靠度函数的随机变量常常具有真实的物理意义,如:时间、循环数、行驶里程等。为便于表述,本文在分析中统称为寿命。
设某装备由n个构件组成,构件的寿命是随机变量 T=(T1,T2,…,Tn),具有联合分布函数为 H(t)=P(T1<t,T2<t,…,Tn<t),且分别具有边缘分布函数(即失效函数,可由试验获取)为Fi(t),i=1,…,n,Copula函数为C,生存Copula函数为C^,则可得
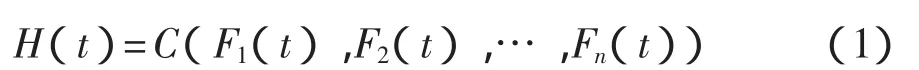
各构件的可靠度函数为Ri(t)=1-Fi(t),系统的可靠度函数为 R(t)。
2.1 串联系统
系统中只要有一个构件发生故障,系统就发生故障,这种系统称为串联系统。串联系统的可靠性框图如图1所示。

图1 串联系统可靠性框图
系统各构件串联时,系统的寿命为各构件中寿命最小的,即 T=min(T1,T2,…,Tn),则系统的可靠度可表示为
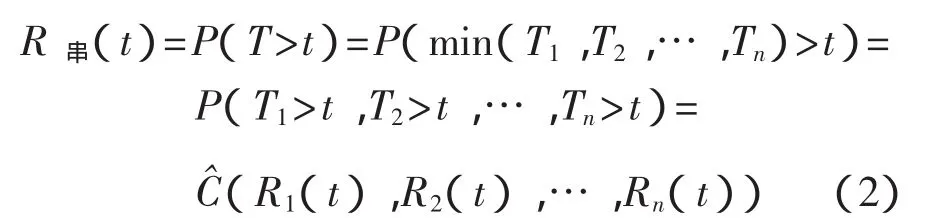
式(2)表示系统可靠度可由生存Copula函数求出。需要说明的是,对于多维的情况,生存CopulaC^不一定是Copula函数。
(1)当各构件独立时,根据随机变量独立的性质
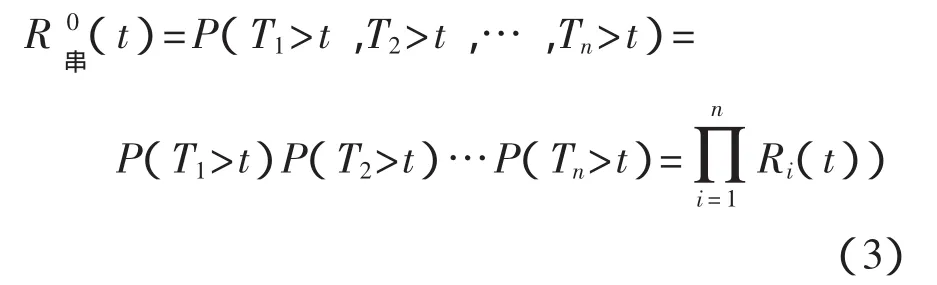
即各构件独立系统的可靠度等于系统中所有构件可靠度的乘积[5]。
(2)当各构件完全相关时,根据最薄弱环节理论,即认为构件可靠度函数是完全相关的两两线性关系此时系统可靠度等于系统中可靠度最小的构件的可靠度[6]。
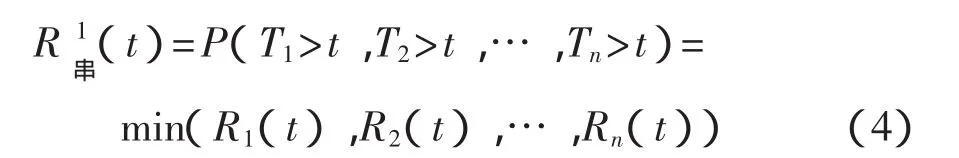
(3)当各构件部分相关时,根据论文对生存Copula C^的介绍,可以通过构造函数找到满足Copula函数定义的C^,该方法简单易用,是计算时的首选,但是在构造Copula函数时会受到一定限制。作为一般情况,下面给出2种通用方法。
1)根据串联系统的定义可知,系统中任意一个构件失效系统就失效,即系统的失效率相当于各构件发生失效事件的集合的并集,因此可以把式(2)做如下变换
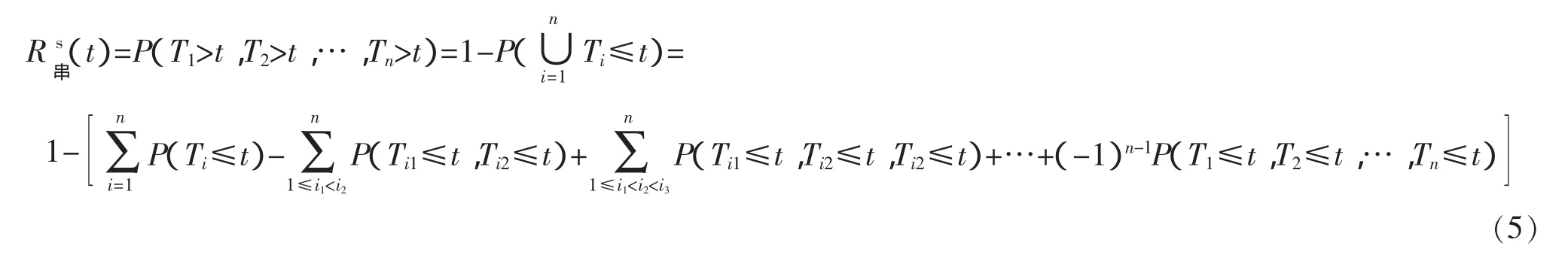
根据 Copula 函数的性质:C(1,…,1,ui,1,…,1)=ui,式(5)变为
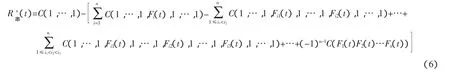
当系统构件较多,即维数n较大时,式(6)中的Copula函数C构成复杂,编程难度和计算量较大,为解决该问题,本文采用下述方法处理高维问题。
2)如图1所示,首先把构件1、2作为一个子系统,求该子系统的可靠度函数,然后该子系统与构件3组成一个子系统,求该子系统的可靠度函数,如此循环求解直至得到可靠度函数
步骤如下
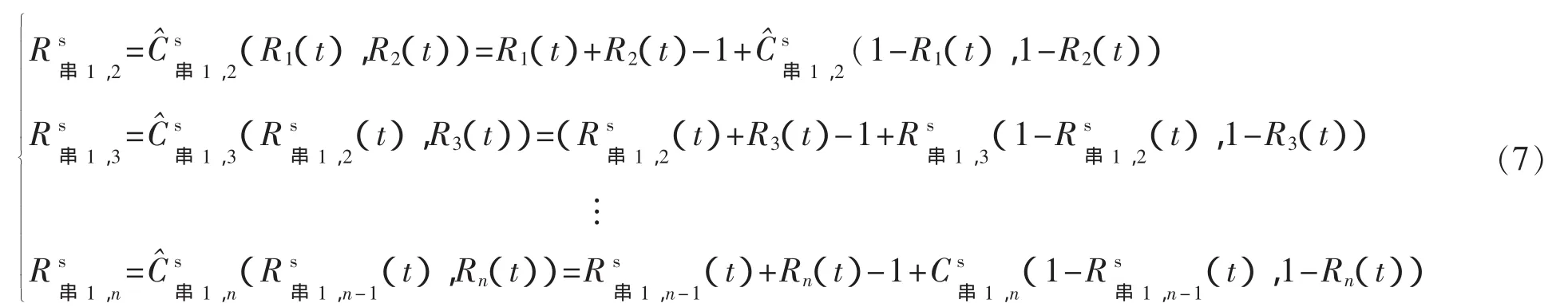
该方法在计算中始终只处理二维问题,C与C^的关系可由式(2)表示,计算量小、便于编程,但是运算过程中各步出现的Copula函数不相同,考虑到简化计算,可以把整体Copula函数的二维形式作为统一的Copula函数进行运算。
(4)串联系统可靠度的界

即各构件完全相关时的可靠度大于各构件独立时的系统可靠度。
在机械系统中,由于各构件之间承受共同载荷冲击、共同的外部工作环境等原因,多表现为正相关性,即在一定应力作用下,一个构件的强度会随着另一构件强度的衰减而衰减[8]。当各构件完全相关时,系统具有最高的一致性;当各构件独立时,系统具有最大的随机性。对于串联系统而言,一致性好对系统有利,因此当各构件完全相关时可靠度最大,当各构件独立时可靠度最小,则式(8)成立
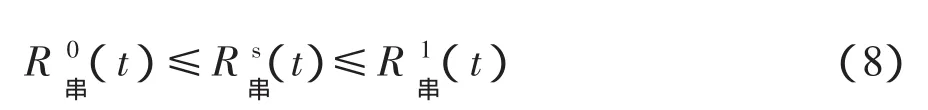
2.2 计算分析
某型车辆行走系统的扭力轴系统由12根扭力轴组成,对整个车辆系统起到支撑和减震的作用,该系统是12维的串联系统。
在行驶过程中,每根扭力轴依次驶过相同的路面,由于车辆对松软地面的压实作用及车辆前部对所受冲击的吸收作用,各扭力轴的行驶工况表现为近似相同,但工况分布又呈现出从前至后恶劣程度逐渐减弱的特点,也就是说各扭力轴表现为部分相关。
在G级路面2挡车速工况下,单个扭力轴的可靠度函数为
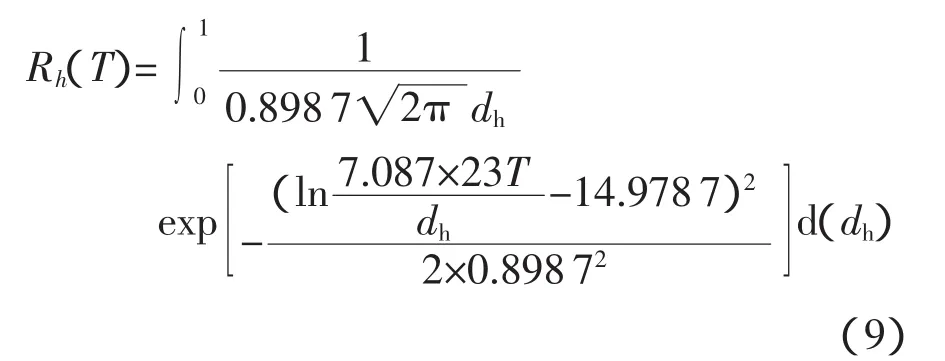
Gumbel Copula函数广泛应用于多元联合生存函数的构造问题,由于生存函数和可靠度函数在数学上具有一致性,因而这类分布同样也适用于联合可靠度函数的构造。且该Copula族属于Archimedean Copula的范畴,构造简单;因此,选取Gumbel Copula函数作为可靠度Copula函数,Gumbel Copula联合分布函数的表达式为
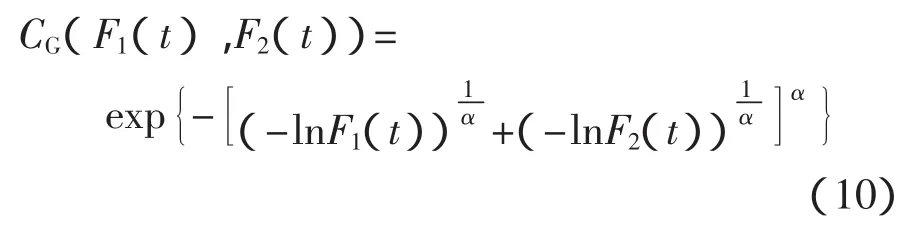
式中:α∈(0,1]。
可以验证,当α=1时随机变量独立,当α减小时随机变量的相关性加强,当α→0时,随机变量趋向于完全相关。参数α可以由极大似然法进行估计。但是由于扭力轴的试验数据较少,因此论文参考其他机械可靠性的数据给出α=0.2的估计值。
根据串联系统可靠度的第2)种算法,经编程,扭力轴系统在G级路面2挡车速工况下的行驶里程与存活概率的关系图如图2所示。
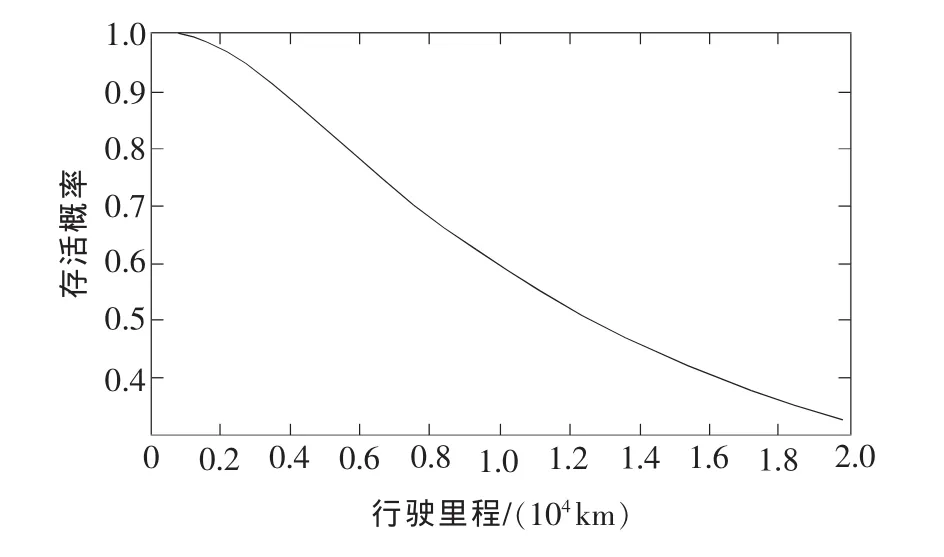
图2 G级路面2挡工况扭力轴系统行驶里程与存活概率的关系图
从图2可以得到,自行火炮在G级路面2挡车速工况下,存活概率等于99%时,扭力轴系统可以行驶1 470 km;当存活概率为90%时,可以行驶3 745km。可见由于各扭力轴之间具有一定的相关性,采用独立性假设计算系统可靠度会造成比较大的误差。
3 结束语
本文介绍了Copula函数的定义和相关性质,并给出了由Copula函数来构造多随机变量联合分布函数的方法。基于该理论对串联系统进行了详细的分析,提出一种计算部件相关的串联系统的系统可靠性方法。该方法考虑了系统中各部件的相关性,使得系统可靠度的计算结果更为合理,为评估装备系统的可靠性提供了一种新方法。
[1]Freuent A M.The safety of structures[J].ASCE Trans.1947(112):125-129.
[2]Wirsching P H.Probability-based fatigue design criteria for offshore structures[R].1983,65(4):42-55.
[3]Martindale S G,Wirsching P H.Reliability-based progressive fatigue collapse[J].Structural Engineering,ASCE,1983,109(8):1792-1811.
[4]Neslen R B.An Introduction to Copulas[C]∥New York:Springer-Verlag,1999(97):145-148.
[5]Benesty J.The committee on fatigue and fracture reliability of the committee on structural safety and reliability of the structural division fatigue reliability[J].Journal of the Structural Division,1982,108(1):3-88.
[6]张明珠.基于Copula函数对相依部件系统可靠度的度量和改进[J].许昌学院学报,2005,24(2):14-17.
[7]董聪,杨庆雄.结构系统疲劳寿命可靠性分析理论与算法[J].航空学报,1993,14(5):247-253.
[8]陈伯真,胡毓仁,顾剑民.结构系统疲劳可靠性分析研究评述[J].力学进展,1996,26(4):500-509.

