基于Lyapunov函数的直驱式风力发电机的无速度传感器直接功率控制

史旺旺，刘 超

（1.扬州大学 能源与动力工程学院，江苏 扬州 225009；2.扬州大学 江苏省水利动力工程重点实验室，江苏 扬州 225009）

0 引言

目前直驱式风力发电省去了故障率较高的变速齿轮箱，提高了系统可靠性，同时可以提高发电机效率、降低成本和噪声、节省成本［1］。因此永磁直驱风力发电系统是变速恒频风力机的重要发展方向之一。

永磁同步电机（PMSG）无速度传感器控制中速度和相位的辨识方法主要有模型参考辨识法、神经网络辨识法和滑模变结构辨识法［1-7］。 文献［7］对上述3种方法进行了对比仿真研究，并得出滑模变结构方法具有更好的鲁棒性的结论。文献［1-3，5，7-8］采用假定旋转坐标法结合数字锁相环研究了无速度传感器控制，并利用“电气稳态”概念［9］在确定锁相误差时忽略了dq坐标系中电流微分项，该方法在接近稳态时效果较好，但忽略了暂态过程的数据，响应速度会降低。由于滑模变结构控制抗干扰能力强，基于电流和磁链模型的滑模变结构控制方法或自适应滑模辨识研究较多［7，10-13］，也有文献用神经网络和模糊等方法提高辨识精度［12］。但滑模变结构辨识中感应电势谐波成分增加，容易造成系统抖动，常用滤波方法来消除，但这会增加延时。

本文采用滑模控制方法控制模型电流，使模型电流误差为零，并使用具有过渡带的近似符号函数，即近似滑模控制，得到了近似正弦波感应电势。由于电机瞬时功率对电机电势、电流、速度和相位不敏感，基于直接功率控制模型利用Lyapunov法进行功率控制，同时辨识出电机角频率，保证了系统稳定，减小了相位跟踪过程中控制器设计难度，提高了电机对转速的响应速度。本文感应电势辨识采用DQ坐标系模型，而功率控制采用直接功率控制模型，并对所提控制策略进行了仿真验证。

1 PMSG的滑模观测器模型

采用电动机惯例，面装式PMSG在DQ坐标系下的定子电压方程为：

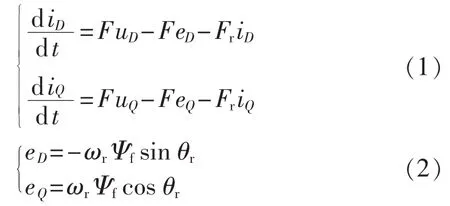
其中，uD、uQ分别为变流器输出电压的 D、Q轴分量；iD、iQ分别为定子电流的 D、Q 轴分量；F=1/L，Fr=R/L，L为发电机定子等效电感，R为发电机定子电阻；eD、eQ分别为发电机 D、Q 轴感应电势；ωr为转子电角速度；Ψf为转子磁链；θr为转子电角度。

参考模型的方程为：

将式（1）和式（3）相减，如果两式中电机参数一致，则得：

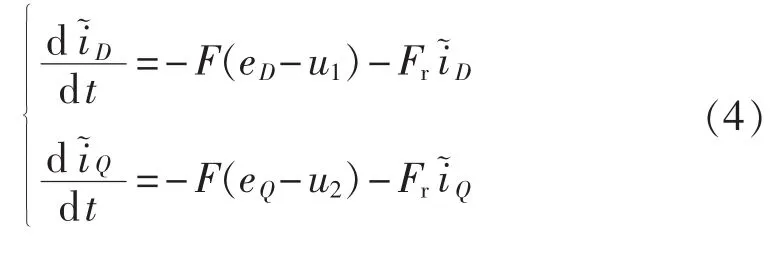
取Lyapunov函数为：

对式（5）求导，得：

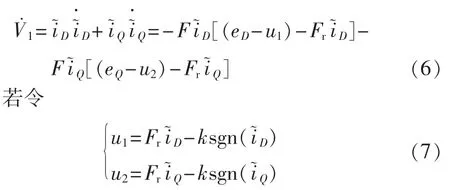
其中，ωr为辨识角频率，ka为主要考虑在动态辨识初期ωr较小时保证系统稳定所加的基值，kb为考虑辨识误差所加的大于1的系数。

当式（4）中的i~D、i~Q收敛到 0 时，可得 u1=uD和u2=uQ，由此可辨识出感应电势。

2 直接功率控制模型

采用上述滑模辨识可以得到eD、eQ的近似值，采用近似符号函数后，可以做到辨识结果近似为正弦波，而且响应速度很快。这样可以利用式（3）进行uD、uQ设计。但设计时无论采用DQ坐标系或dq坐标系，都需要电机感应电势的角频率和相位值，对它们的识别一般利用锁相环进行，响应时间比较长，使得在暂态过程中给定值出现误差，对控制不利，甚至出现控制信号频率不能跟踪感应电势频率的情况。控制信号的频率和相位误差影响了电机电流的频率，进而影响了感应电势的辨识。瞬时功率模型对电压电流相位不敏感，该模型只用到角频率，降低了设计难度，同时响应速度更快。

根据瞬时功率的定义，令

对式（10）中p、q求导，同时考虑到电网电压三相对称时满足：和为电网电压角频率。得到功率控制方程为：

在三相对称条件下，PMSG功率模型与坐标系无关。令 up=u1uD+u2uQ，uq=u1uQ-u2uD。 将 up、uq看作控制量，在求出up、uq后，利用其定义可求出控制量 uD和 uQ，即：

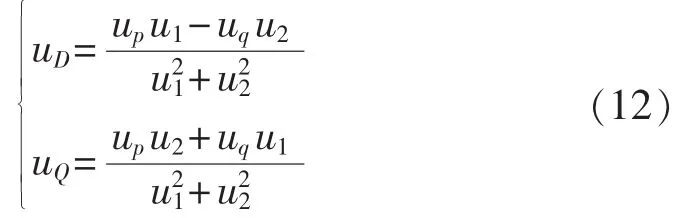
由于 up、uq为直流量，式（11）直接利用了 u1、u2，因此控制量uD、uQ与感应电势同频率。

3 基于Lyapunov法的控制器设计

功率控制的目标是p跟踪设定值 p0，q跟踪设定值 q0，设为角频率ω的观测值，为观测误差。为使功率控制和ω观测误差为0，定义如下Lyapunov函数：

其中，s1、s2为有功功率和无功功率控制误差；C1、C2为s1、s2的积分项的加权系数，kω为观测误差的加权系数，分别表示在Lyapunov函数中所占的权重。

对 Lyapunov函数 V2求导，将 ω=ω^+ω~ 代入式（11）得：

其中，kp、kq为有功功率和无功功率控制的比例系数。

4 仿真验证及分析

为验证本文所提出的直接功率模型以及控制算法的有效性，使用MATLAB进行仿真，仿真时电机电阻 R=0.6 Ω，电感 L=5 mH，则 F=200，Fr=120。 为测试对转速的响应能力，仿真时在0.1 s时将感应电势频率从50 Hz降为20 Hz。图1为实际电势和近似滑模辨识的电势。从图中可以看出两曲线基本重合，说明辨识效果良好。

图1 电机实际与辨识感应电势Fig.1 Practical and identified induced electromotive force of PMSG

图2为在辨识出的电势的基础上利用直接功率控制模型设计的控制电压，结果说明控制电压能跟踪电势频率的变化。图3为电机D轴电流。

图2 控制电压Fig.2 Control voltage

图3 电机电流Fig.3 Current of PMSG

图4为p0=-100kW、q0=0kvar的电机输出功率，由于本文采用电动机惯例，功率的设定值取负值，表示电机发出的功率。由图4可以看出，在Lyapunov采用功率误差积分后，输出功率无误差，且响应速度很快。

图5为采用角频率自适应率的频率输出。可以看出能以较快的速度跟踪频率的突变，但在50 Hz时有一定的误差，表明该自适应率不适用于角频率测量，但用在基于Lyapunov函数设计时是有效的，可以保证系统收敛。

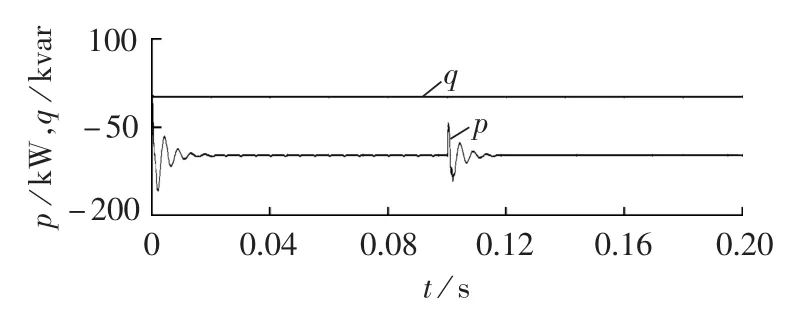
图4 电机功率输出Fig.4 Power output of PMSG

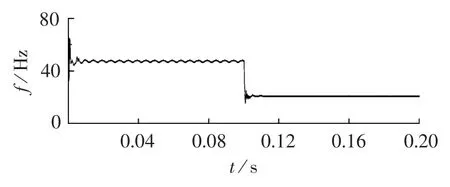
图5 观测频率Fig.5 Identified frequency

5 结语

直驱式风力发电中PMSG的电机转速变化大，在无速度传感器控制中对相位辨识要求高，对控制提出了更高的要求。本文在滑模辨识基础上采用近似滑模控制对电机感应电势进行辨识，获得了近似正弦波感应电势。利用直接功率控制模型进行功率控制，降低了相位跟踪过程中控制器的设计难度，提高了电机对转速的响应速度。对于直接功率控制中需要的角频率，利用Lyapunov函数给出角频率的自适应率，取消了数字锁相环，提高了控制响应速度。仿真结果表明，本文采用的基于Lyapunov函数的功率控制和角频率自适应方法，可以快速地对电机功率进行控制，较适用于直驱式风力发电中PMSG控制，如功率控制和最大功率跟踪等。但本文提出的方法需要精确的电机模型，如果在控制中对电机参数进行辨识，则效果会更好。