基于预仿真策略的变电站培训仿真系统
张炳达,李银芝
(天津大学 智能电网教育部重点实验室,天津 300072)
0 引言
目前,变电站培训仿真系统已成为一种培训变电工人的有效工具,其中数字物理混合型变电站培训仿真系统备受关注[1-4]。这种培训仿真系统对一次系统采用全数字仿真,对二次系统使用全部真实设备。为了能使二次系统真实设备正常运行,要求一次系统数字仿真部分提供的电压互感器二次侧电压信号和电流互感器二次侧电流信号具有实时性[5-8]。
变电站一次系统仿真模型不仅涉及断路器、隔离开关、母线、变压器、地线等设备,而且还要在输电线路部分插入若干个故障模型。为降低数字一次系统的建设成本,本文采用贝瑞隆等值电路描述输电线路,把一次系统仿真模型分解成1个站内仿真模块、若干个线路仿真模块和负荷仿真模块;用逻辑分析法决定电流互感器中的真实电流,使站内仿真模块仅包含变压器、母线节点和馈线端点;采用易于并行化的多项式预条件共轭梯度(PCG)法进行仿真计算,便于用多微处理器系统加以实现。为避免一次系统网络参数突然变化引起的计算风暴对实时仿真的干扰,提出了一种计算模块独立于输出模块的预仿真策略。
1 变电站仿真模型的分块
为模拟输电线路不同位置的故障,将输电线路分成若干段,且在段间加入如图1所示的故障模型。
在图 1 中,Ra、Rb、Rc用于模拟断线故障,Rae1、Rbe1、Rce1、Re1和 Rae2、Rbe2、Rce2、Re2用于模拟短路故障,其中各电阻的取值因故障性质而异。
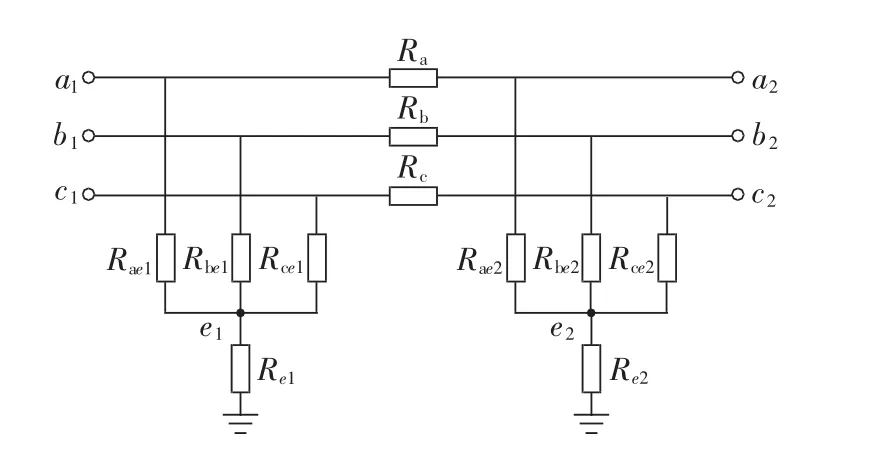
图1 故障模型Fig.1 Fault model
若输电线路采用集中参数模型且分成3段,负荷为Y接法,每增加1回输电线,变电站仿真模型的节点数就增加28个,这严重制约了仿真变电站的规模。
对三相输电线路采用小损耗模型,并通过相模变换和相模反变换形成贝瑞隆等值电路[9-10],如图2所示。
图2中的相间阻抗、对地阻抗分别为:
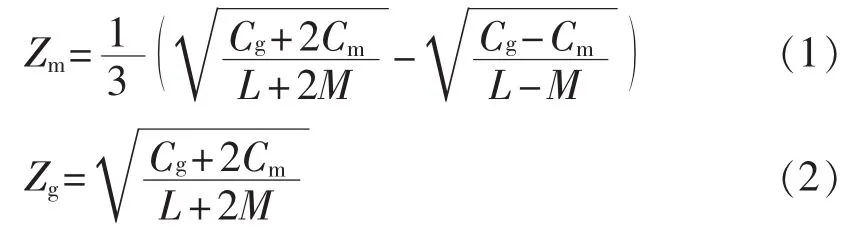
其中,L、Cg分别为各相输电线的自感和对地电容,M、Cm分别为各相输电线间的互感和电容。
图2中各相等效电流源与输电线路首末端(k和m端)电压、电流之间的关系为:


图2 输电线路的贝瑞隆等值电路Fig.2 Bergeron model of transmission line

其中,Zm1和Zm2分别为时间常数τm1和τm2对应的相间阻抗。
由于很难使仿真步长Δt同时为时间常数τm1和τm2的整数倍,采用线性插值法确定等效电流源的数值。
由图2可见,线路两端电气量的求解过程是解耦的。利用这一性质,可以将变电站仿真模型分解为1个站内仿真模块、若干个线路仿真模块和负荷仿真模块。
2 站内仿真模块的简化
由于二次系统设备仅需要母线处电压、变压器两侧的电流和馈线电流等,可以对站内仿真模块进行适当的简化。
图3给出了1台双绕组变压器在某变电站中与母线的连接关系。变压器的各种保护仅涉及其两侧的电流 i1a、i1b、i1c、i2a、i2b、i2c,以及母线 1、母线 2、母线 3处的电压,并不涉及其他设备的电流。若把变压器与母线连接部分的等效电路描述成图4,将图3中p、q、r、s处可能出现的短路故障转移到母线处或变压器两侧,则电流互感器中的实际电流可以用逻辑分析法来决定。
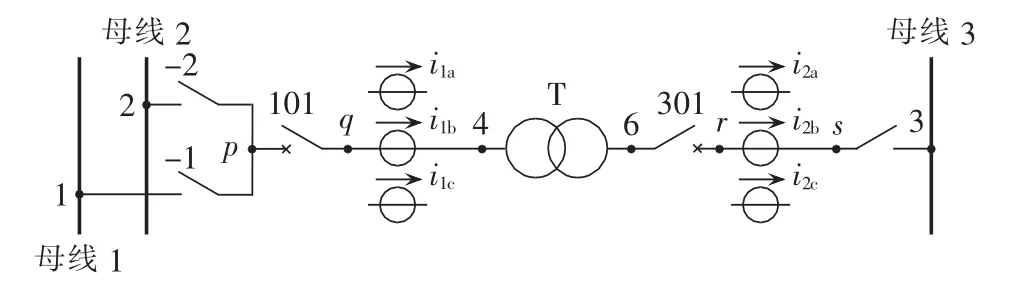
图3 变压器与母线连接示意图Fig.3 Connections between transformer and buses

图4 变压器与母线连接部分的等效电路Fig.4 Equivalent circuit of connections between transformer and buses
图4中 的 Ra14、Rb14、Rc14、Ra24、Rb24、Rc24、Ra63、Rb63、Rc63分别表示图3中节点1-4、节点2-4、节点3-6的连通性。连通时电阻取值很小,不连通时电阻取值很大。
短路故障转移的原则为:以电流互感器为分界点,若短路故障点至少与母线或变压器一方连通,优先往同侧方向移动,否则不予考虑。
当同一母线或变压器两侧的等效短路故障仅来自同侧或异侧,各电流互感器中的实际电流可用逻辑分析法决定。如变压器高压侧电流互感器中的电流为:
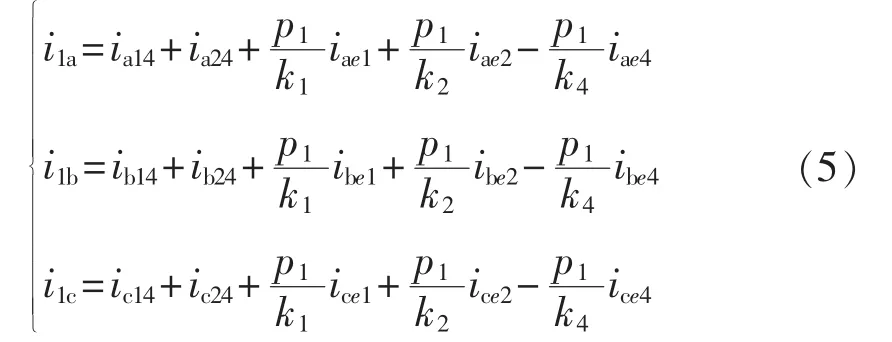
其中,k1、k2、k4分别为母线 1、母线 2、变压器高压侧接受的异侧短路故障点总数;变压器高压侧电流互感器有移动的短路故障点通过时p1=1,否则p1=0。
同样,采用短路故障转移法和电流逻辑分析法使馈线始端部分的等效电路得到简化。由此,站内仿真模块仅包含变压器、母线节点和馈线端点,其节点导纳矩阵的维数大幅降低。
3 变电站仿真模型的求解
无论是站内仿真模块、线路仿真模块,还是负荷仿真模块,暂态解等值电路的节点电压方程都有相同的形式,即:

其中,Y 为导纳矩阵,u(t)为节点电压,i(t)为注入电流源,I为等效电流源。
共轭梯度(CG)法[11]是目前求解方程组最有效的迭代法之一,其基本思想是把共轭性与最速下降方法相结合,利用已知点处的梯度构造一组共轭方向,并沿这组方向进行搜索,最终求出目标函数的极小点。用CG法求解式(6)的过程如下:
步骤 1 设 b=i(t)-I,t=t0,u(0)(t)=0,迭代终止常数 ε>0;
步骤2令迭代次数k=0;
步骤 3 计算残差 r(k)=b-Yu(k)(t),梯度 p(k)=r(k);
步骤 4 当‖r(k)‖>ε 时,转步骤 6;
步骤5计算u(t)近似值的迭代过程结束,使t=t0+Δt,u(0)(t)=u(t-Δt),计算新的注入电流源i(t)和等效电流源 I,转步骤 2;
步骤 6 计算 u(t)新的近似值 u(k+1)(t)=u(k)(t)+αkp(k)和新的残差 r(k+1)(t)=r(k)(t) -αkYp(k),其中 αk=-(r(k),r(k)) /(p(k),Yp(k)),(·,·)表示内积,后同;
步骤 7 计算新的梯度 p(k+1)=r(k+1)+ βkp(k),其中βk=(r(k+1),r(k+1)) /(r(k),r(k));
步骤8令k=k+1,转步骤4。
在计算u(t)近似值的迭代过程中,绝大部分是求内积运算和矩阵与向量乘运算,这些运算都可以分块进行,且各块运算是完全独立的。因此,CG法易于并行化。
由于舍入误差的存在,CG法的收敛速度依赖于系数矩阵Y的特征值分布情况。如果特征值分布相对集中,那么收敛的速度很快,反之收敛的速度很慢,甚至有可能不收敛。为了加快收敛速度,构造一个“近似于”Y的预条件M,使M-1Yu=M-1b中的M-1Y“近似于”单位矩阵,保证其特征值分布在1的周围。
由于矩阵Y具有对角占优的特点,可采用多项式变换法确定预条件M[12-13]。若采用一阶多项式变换法,则预条件M的逆为:
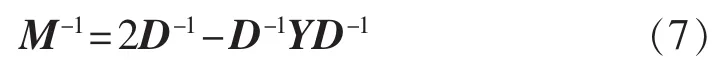
其中,D为矩阵Y的对角阵。
由于矩阵M-1的每个元素可表示为:

故M-1保持了原矩阵Y中“0”元素的分布。
可以证明,M-1Y中的“0”元素分布与原有矩阵Y的“0”元素分布并不一致。若令G=M-1Y,对Gu=M-1b采用CG法求解,则不能充分利用矩阵Y的稀疏性。本文以残差 r(k)=M-1(b-Yu(k)(t))为目标函数,求取其极小点,求解过程与求解式(6)的过程略有不同。
a.步骤 3 变为:计算残差 r(k)=b-Yu(k)(t),梯度p(k)=M-1r(k)。
b.步骤 6 变为:计算 u(t)新的近似值 u(k+1)(t)=u(k)(t)+αkp(k)和新的残差 r(k+1)(t)=r(k)(t)-αkYp(k),其中αk=-(r(k),M-1r(k)) /( p(k),Yp(k))。
c. 步骤 7 变为:计算新的梯度 p(k+1)=M-1r(k+1)+βkp(k),其中 βk= (r(k+1),M-1r(k+1)) /(r(k),M-1r(k))。
可见,PCG法保持了CG法易于并行化和充分利用“0”元素的特点,便于用多微处理器系统加以实现。
4 预仿真策略
为实现实时仿真,计算模块、输出模块在规定的时间点上轮流工作,且要求计算模块的计算时间tc不能超出仿真步长Δt。但是,在这种计算模块、输出模块轮流运行的定点仿真模式中,一次系统稳定运行时,求解的迭代次数k较少,计算时间tc较短;而当一次系统的网络参数发生变化时,求解的迭代次数k增多,计算时间Tc较长,出现严重的计算风暴。
若仿真步长Δt大于稳定运行时的最小计算时间Tcmin且小于网络参数变化时的最大计算时间Tcmax,可采用预仿真策略[14-15],其基本思想如下:计算模块完成一次系统仿真模型的求解,将结果依次放入队列;当队列处于满状态时,计算模块暂停工作;输出模块以仿真步长Δt为时间间隔从队列中取出数据,用于模拟电压互感器二次侧的电压信号和电流互感器二次侧的电流信号。在这种计算模块、输出模块各自独立运行的仿真模式中,当一次系统稳定运行时,计算模块向队列中存数据的频率比输出模块从队列中取数据的频率要高,队列最终处于满状态;当一次系统的网络参数发生变化时,网络的过渡过程现象不能立刻反映到电压互感器二次侧电压和电流互感器二次侧电流上,队列越长,延时越严重。但是,如果队列的长度太短,由于Tcmax>Δt,有可能造成队列处于空状态。
假设1个工频周期T内有N个Δt,累计迭代次数为K,1次迭代过程的机器周期数为P,微处理器的时钟频率为fclock,则完成1个工频周期仿真所需的计算总时间为:

如果输出模块比计算模块迟1个工频周期T启动,队列的长度设为N,且Tc≤T,则队列永远处于满状态。这样网络的过渡过程现象仅迟1个工频周期T发生,对培训仿真系统而言是可以接受的。
在仿真中,认为开关分闸在电流过零时才会发生,存在三相不同时分闸现象。对于中性点接地系统,开关分闸时发生3次网络参数变化,而对于中性点不接地系统,仅发生2次网络参数变化。因此,应考虑各种开关分闸情况,以工频周期内的最大累计迭代次数Kmax来选择微处理器。
若微处理器的时钟频率fclock已确定,完成工频周期仿真的最大计算时间为:

在计算模块、输出模块轮流运行的定点仿真模式中,工频周期内的最大累计迭代次数为kmaxN(kmax为1个仿真点上的最大迭代次数),则完成工频周期仿真的最大计算时间为:
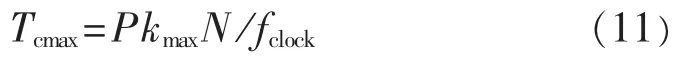
对于多微处理器系统,完成工频周期仿真的最大计算时间Tcmax还与微处理器的数量有关。因此,无论采用CG法还是PCG法,由于kmaxN≫Kmax,预仿真策略都能降低对微处理器运算速度的要求;或可减少微处理器数量,甚至可仅用1个微处理器;或可扩大仿真变电站的规模。
5 应用实例
图5是一个全部采用单母分段接线的110 kV/35 kV港口仿真变电站,具有2回110 kV馈线、4回35 kV馈线和2台变压器。将输电线路分成3段,且在段间加入故障模型。同时,考虑输出模块的输出量仅涉及电压互感器二次侧电压和电流互感器二次侧电流。通过贝瑞隆法和短路故障转移法,把一次系统仿真模型分成1个64节点的站内仿真模块、12个14节点的线路仿真模块和6个12节点的负荷仿真模块。
针对港口仿真变电站的一次系统仿真模型,在Altera的QuartusⅡ仿真平台上编写了基于CG法和PCG法的计算程序。其中,仿真步长Δt=10 μs(1个工频周期2 000个仿真点),迭代收敛精度ε=10-8。为了得到工频周期内的最大累计迭代次数Kmax或kmaxN,模拟了变压器故障、线路故障、母线故障。表1给出4种算法的一次迭代过程的机器周期数P、工频周期内的最大累计迭代次数Kmax或kmaxN,并按微处理器的时钟频率fclock=100 MHz估计了完成工频周期仿真的最大计算时间Tcmax。
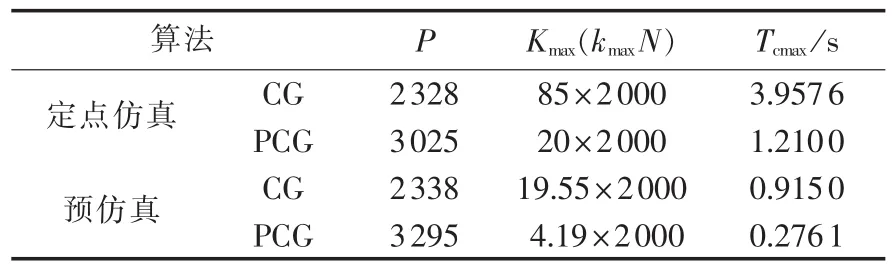
表1 4种算法的对比Tab.1 Comparison of four algorithms
由表1可以看出,虽然PCG法的一次迭代过程机器周期数比CG法有所增加,但无论是定点仿真还是预仿真,PCG法的工频周期内的最大运算量都有所减少,约为CG法的1/4。进一步而言,预仿真下PCG法的工频周期内的最大运算量是定点仿真下CG法的1/16。
EP3C80属于CycloneⅢ的FPGA系列,具有低功耗和大容量的特点。通常,1片EP3C80能较好地模拟8个具有64×64位乘法器的计算单元。由表1可推论,对于PCG法,采用定点仿真需8片EP3C80,而采用预仿真时仅需要2片。
在仿真步长内,站内仿真模块、线路仿真模块、负荷仿真模块之间不需要数据通信,且线路仿真模块是联系站内仿真模块与负荷仿真模块的桥梁。为减少模块之间的通信量,将线路仿真模块、负荷仿真模块放置在一片EP3C80中,而站内仿真模块单独放置在另一片EP3C80中。同时,使用数模转换器和功率放大器将数字式一次系统的数字信号变成互感器二次侧的模拟信号,利用模拟开关设备接受真实二次设备的分合闸信号,并将其状态传输给数字式一次系统。
大量的仿真实验表明,基于预仿真策略的数字式一次系统,在二次真实设备的配合下,不仅能够模拟变电站的各种正常运行方式,而且能模拟各种短路故障、断路器故障、保护故障,营造出与真实变电站高度相似的环境。

图5 港口仿真变电站主接线Fig.5 Main connections of simulative harbor substation
6 结论
a.PCG法充分利用了一次系统节点导纳矩阵稀疏性的特点,使仿真模型的求解运算量是一般CG法的1/4。
b.基于计算模块独立于输出模块的预仿真策略把计算风暴分散到1个工频周期内的各个仿真点上,使工频周期的最大累计迭代次数是定点仿真模式的1/4。
c.通过贝瑞隆法、短路故障转移法与电流逻辑分析法、PCG法、预仿真策略,使复杂的变电站一次系统仿真能在廉价的多微处理器系统中完成。

