等角扇形束投影的CT重建算法研究
敖 波,曾亚斌,吴 伟,金信鸿,祝忆春
(1.无损检测技术教育部重点实验室(南昌航空大学),南昌 330063;2.中国联合网络通信有限公司江西省分公司,南昌 330096)
0 引言
X射线计算机断层扫描技术(Computed Tomography,CT)是通过对物体进行不同角度的射线投影测量而获取物体横截面信息的成像技术。它能在对被检物体无损伤条件下,以二维断层图像或三维立体图像的形式,清晰、准确、直观地展示被检测物体内部的结构、组成、材质及缺损状况,被誉为当今最佳无损检测技术[1-2]。CT技术的核心是由投影重建图像的理论,其实质是由扫描所得到的投影数据反求出成像平面上每个点的线衰减系数值[3-4]。滤波反投影法(Filtered Backprojection,FBP)是最常用的CT重建算法,滤波器和内插方式的选取是最重要的。
二维CT投影扫描方法有平行束扫描和扇形束扫描,扇形束扫描效率要远高于平行束扫描,实用中扇形束扫描使用最多。根据扇形束扫描探测器的分布特点分为等角射线型(探测器分布在等角的弧线上)和等距射线型(探测器在直线上呈等距分布)2 种[5]。Li等[6]讨论了等角分布扇形束扫描中角度大小对重建质量的影响。杨民等[7]在等距分布情形下,针对旋转中心对重建质量的影响,根据投影正弦图提出了自动测量旋转中心的方法。
由于CT重建不可避免地出现伪像,而伪像的处理方法是CT的商业机密,商用CT一般对CT重建图像往往进行加密处理,不利于用户的后续处理;因此,针对本实验室的CT设备的线阵探测器获取的等角扇形束投影数据,有必要研究等角扇形束投影的CT重建。
1 扇形束投影CT重建算法
1.1 等角扇形束投影几何
扇形束投影探测器的布置方式有等角射线型和等距射线型。图1为等角扇形束投影几何,特点是相邻探测器单元与射线源之间的夹角为固定角度。S为射线源,物体旋转中心为O,β为中心射线SO与物体旋转坐标系的夹角。当旋转工作台旋转时,β角将从0变到359°,若投影角度间隔为1°,由此可得到360个不同角度下的投影。

图1 等角扇形束投影几何Fig.1 Geometry of equiangular fan beam projection
1.2 投影数据分布图像
物体沿角度β下路径l的射线投影pβ定义为

其中:I0为入射射线强度,I为穿过工件后的射线强度。当采用扇形束投影几何时,每个角度β下的投影是关于探测器位置的分布函数,β从0°到359°,就可得到不同角度下的投影分布。CT的任务是根据不同角度下的投影数据,反求被积函数μ,得到μ分布(密度分布)图像。
考虑到反投影重建算法的基础是认为断层图像上任何一点的值等于该平面上经过该点的全部射线投影之和。必须首先得到所有角度下的投影数据,以角度为横坐标,不同探测器获得的投影为纵坐标,得到投影分布图像。图2为对C/C复合材料扇形束扫描后的投影分布图像,其中投影角度数量为1024,角度间隔为360/1 024,每个投影角度下的投影数为413个。
1.3 FBP 算法
滤波反投影重建公式为

根据上式可知,滤波反投影重建是先把不同角度下获得的投影数据分别进行卷积滤波运算,得到各角度下滤波后的投影;然后针对重建平面上的每一点,把所有经过该点的射线投影进行反投影运算得到该点的线衰减系数值;最后把线衰减系数分布经过映射后得到断层图像。

图2 投影分布图像Fig.2 Projection image
算法步骤如下:
1)把在固定角度β下测得的投影p(xr,β)经过滤波器h滤波,得到滤波后的投影g(xr,β)。
2)对于每一个β,把g(xr,β)反投影于满足xr=rcos(θ-β)的射线上的所有各点(r,β)。
3)将步骤2)中的反投影值对所有0<β≤2π进行累加,得到重建后的图像。
2 重建结果与分析讨论
2.1 CT系统重建结果
实验材料为三点弯曲实验后的C/C复合材料,实验设备为重庆大学研制的线阵探测器CT系统CD-300BX,用于获取不同角度下的投影数据(图3a),探测器采用LDA探测器(等角扇形束分布),探测器单元总个数为432,A/D位数为20位,系统包括后准直器、探测器、信号采集处理和信号转换电路等。扫描方式为三代CT扫描,射线能量为80 kV,管电流为2 mA,焦点尺寸为1 mm,视场直径为80 mm,重建矩阵为512×512,进行射线投影数据采集,投影角度为1 024,角度间隔为360/1 024,每个角度下探测器单元个数为413,得到某截面投影数据分布图像如图2所示。利用CT系统自带重建功能(S-L滤波器、线性内插)重建结果如图3b所示,从重建结果可以看出内部存在裂纹和空隙。由于反投影法的本质是把取自有限物体空间的投影均匀地反投影到射线所及的无限空间的各点;因此,原先像素值为零的点反投影后不为零,产生星状伪迹。另外,由于CT重建算法的原因,目标周围不可避免地存在环状伪影。系统重建结果的不足是由于数据加密原因难以得到原始重建数据。

图3 三代CT扫描与重建Fig.3 The third generation of CT scanning and reconstruction
2.2 重建质量影响因素分析
扇形束投影的CT重建图像质量取决于探测器系统的性能、数据校正、射线源、滤波函数、频域插值方式等。当扇形束投影CT成像系统固定时,滤波函数和频域插值对重建质量具有重要的影响[8]。
1)滤波函数的选择。
滤波函数指滤波器的系统函数H(ρ)。理想的滤波器H(ρ)=|ρ|是频带无限的滤波函数,在无穷积分区间上积分发散,根据佩利一维纳准则,该理想滤波器是不可实现的。常用滤波器有[9]:
(1)R-L(Ram-Lak)滤波函数。
由于理想滤波器频带无限,通过窗函数截断理想滤波器,得到近似理想滤波器。

其中,矩形窗函数rect(ρ/2B)为

其中d为采样间隔。
R-L滤波函数结构简单,重建的图像轮廓清楚。缺点是由于在频域中用矩形窗函数截断了滤波函数,会造成振荡响应,即Gibbs现象。
(2)S-L(Shepp-Logan)滤波函数。
由于R-L滤波器在|ρ|=1/2d处混叠严重,为了减小|ρ|=1/2d处的混叠,把R-L滤波器与sinc(ρ/2B)进行卷积,就得到S-L滤波器。

其中,sinc(ρ/2B)=sin(ρ/2B)/(ρ/2B)。
用S-L滤波器重建的图像中振荡相应较小,对含噪声的数据重建出来的图像质量也较R-L滤波函数要好。但是由于该滤波函数在低频段偏离了理想的滤波函数|ρ|,因而重建图像在低频段的响应不如R-L滤波函数[10]。
(3)Hamming和Hanning滤波函数。
将R-L滤波器与Hamming窗进行卷积而得到Hamming滤波器。
将R-L滤波器与Hanning窗进行卷积得到Hanning滤波器。
图4是对图2进行R-L滤波后得到的结果。

图4 R-L滤波后图像Fig.4 Projection of R-L filtering
2)内插方式。
常用的内插方式有紧邻内插和线性内插[9]。紧邻内插是将nd邻近±d/2范围内的函数值都认为等于nd处的函数值,即
p(xr)=p(nd),(n-1/2)d < xr< (n+1/2)d;线性内插是将nd邻域±d范围内的函数值取

紧邻内插和线性内插都是不精确的内插,精确内插函数是sinc函数,但运算复杂。线性内插和紧邻内插是CT重建中经典的内插方式。
3)重建图像质量客观评价
为了客观比较重建图像的质量,采用峰值信噪比和平均梯度来评价图像质量。
峰值信噪比(Peak Signal to Noise Ratio,PSNR)是最广泛使用的评价图像质量的客观标准,定义如下:

平均梯度是指图像的边界或影线两侧附近灰度有明显差异,即灰度变化率。平均梯度定义如下:
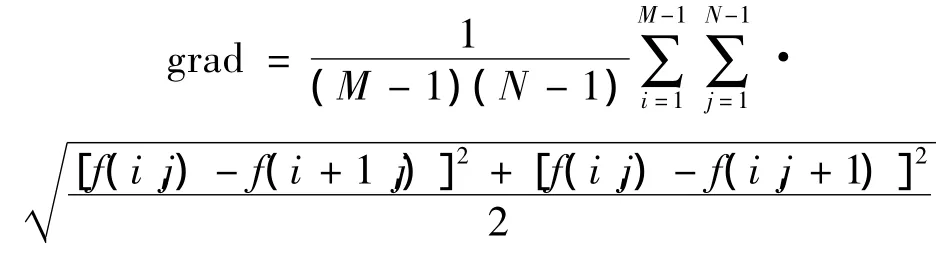
其中:f(i,j)为图像的第i行,第j列的灰度值;M、N分别为图像的总行数和总列数。
平均梯度反映了图像微小细节反差变化的速率,可以用于表征图像的相对清晰程度。平均梯度越大,图像层次越多,也就越清晰。
2.3 本算法重建结果
为了便于对比实验结果,本实验所用计算机处理器为 Intel Pentium(R)D CPU 2.8 GHz,重建软件平台为Matlab6.5。
为了分析滤波器类型对重建质量的影响,将投影数据按顺序取出,导入自开发的CT重建程序,滤波反投影过程中分别选用R-L滤波器、S-L滤波器、Hamming滤波器和Hanning滤波器,内插方式分别采用了经典的线性内插和紧邻内插,重建矩阵大小为413×413。内插方式为线性内插时的重建结果如图5所示。对图5中图像进行PSNR和平均梯度计算,为了减少重建视场外的噪声影响,图像统计计算区域为图5a中白色方框区域,得到统计结果如表1所示。从表1中数据可以看出,当内插方式固定时,R-L滤波器重建图像的PSNR和平均梯度值最大。Hamming滤波器和Hanning滤波器重建图像的PSNR、平均梯度值与R-L滤波器、S-L滤波器差异较大,图像直观表现在图像模糊。对比结果得出R-L滤波器重建图像轮廓最清晰。
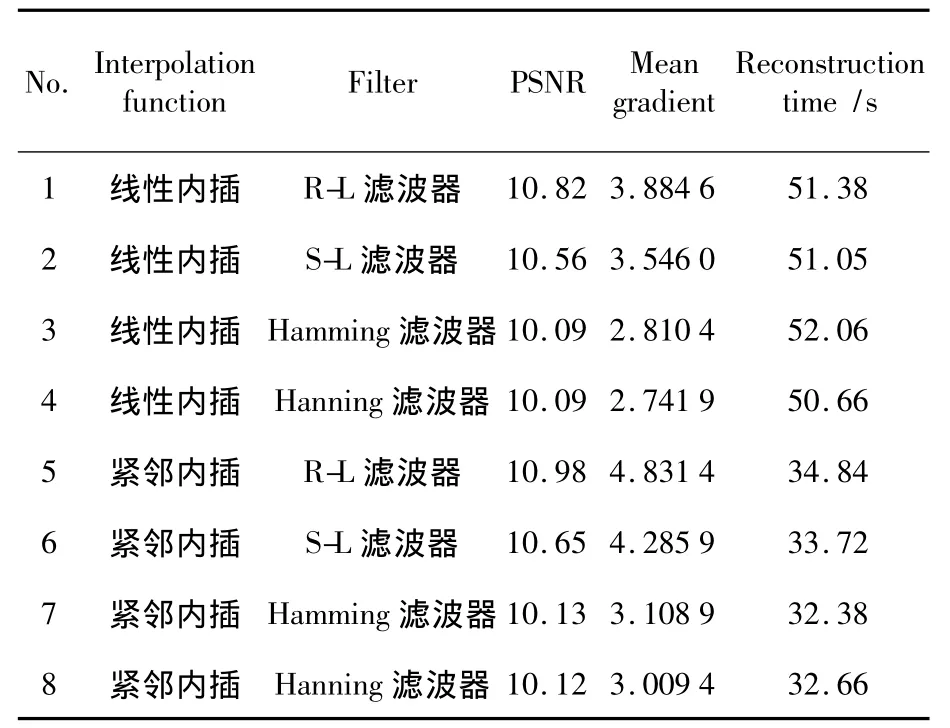
表1 不同滤波器的重建图像定量比较Table 1 Quantitative analysis of reconstruction images of different filters
为了分析内插方式对重建图像质量的影响,滤波反投影过程中选用R-L滤波器,内插方式分别采用线性内插、紧邻内插和Spline内插,重建矩阵大小为413×413,重建结果如图6所示。对图6中图像进行PSNR和平均梯度计算,为了减少重建视场外的噪声影响,图像统计计算区域为图5a中白色方框区域,得到统计结果如表2所示。从表2中数据可以看出,当采用R-L滤波器时,Spline内插时重建图像的PSNR最大,但Spline内插运算复杂,耗时,而紧邻内插时重建图像的平均梯度值最大。综合考虑PSNR、平均梯度和重建时间3个因素,不难得出紧邻内插时重建图像质量最好。
将选用R-L滤波器和紧邻内插方式重建图像与CT系统(图3b,也对应图5b图像)进行对比,本研究的重建结果已达到了CT系统的重建质量,且能得到原始重建数据,有利于后续处理。

图5 线性内插时不同滤波器重建图像对比Fig.5 Comparing of reconstruction images of different filters for linear interpolation

图6 不同内插方式重建结果对比Fig.6 Comparing of reconstruction images for different interpolation

表2 不同内插方式时重建图像定量比较Table 2 Quantitative analysis of reconstruction images of different interpolations
3 结论
1)通过滤波反投影重建算法研究,实现了等角扇形束投影的CT重建。
2)利用CD-300BX获取C/C复合材料扇形束CT投影数据,通过自行开发的重建算法进行了CT重建实验验证。分析了滤波器、内插方式对重建图像质量的影响,引入了PSNR和平均梯度对重建结果进行定量客观评价,通过实验结果对比得出采用R-L滤波器、紧邻内插时重建图像质量最好。
3)本研究重建算法的重建质量达到CT系统的重建质量。
[1]张朝宗.工业CT技术和原理[M].北京:科学出版社,2009:3-10.
[2](美)Jiang Hsieh.计算机断层成像技术原理、设计、伪像和进展[M].张朝宗,郭志平,王贤刚,等译.北京:科学出版社,2006:3-12.
[3]Kak A C,Slaney M.Principles of computerized tomographic imaging[M].IEEE Press,1999:49 -92.
[4]Herman G T.Fundamentals of computerized tomography:imagereconstruction from projections[M].Springer,2009:1 -26.
[5]张聪哲,李晓苇,杨昆.扇束等角型CT与等距型CT的比较研究[J].CT理论与应用研究,2013,22(2):215-223.
[6]Li H J.X-ray chest image reconstruction by radon transform simulation with fan-beam geometry[J].Measurement,2010,43:447-453.
[7]Yang M,Pan J,Zhang J H,et al.Center of rotation automatic measurement for fan-beam CT system based on sinogram image features[J].Neurocomputing,2013,http://dx.doi.org/10.1016/j.neucom.2012.08.066.
[8]张斌.滤波反投影图像重建算法中插值和滤波器的研究[D].太原:中北大学,2009:15-25.
[9]庄天戈.CT理论与算法[M].上海:上海交通大学出版社,1992:63-71.
[10]张顺利,李卫斌,唐高峰.滤波反投影图像重建算法研究[J].咸阳师范学院学报,2008,23(4):47-49.
———《扇形的认识》教学廖

