基于RBF神经网络与LMD的滚动轴承故障诊断方法

莫 燕，孙 伟，熊邦书

(1.南昌航空大学 信息工程学院，南昌 330063;2.中国直升机设计研究所直升机旋翼动力学国防科技重点实验室，江西景德镇 333001）

0 引言

目前，直升机在军用和民用中的作用日益突出，其在飞行过程中的可靠性和安全性问题受到广泛地重视。直升机在飞行过程中通过传动系统将发动机动力传给主旋翼和尾桨，其传动系统关键零部件会承受较大的载荷，容易发生故障;且此类关键部件无冗余备份，一旦发生故障常会导致灾难性的后果。因此，研究直升机传动系统故障诊断及预测对提高其运行时的可靠性和安全性具有重要的现实意义及重大的国防战略价值。

直升机传动系统关键零部件产生故障，如滚动轴承，将直接影响其稳定运行。目前，振动信号分析法是直升机传动系统状态监控和故障诊断的主要方法［1-3］。然而，由于滚动轴承产生的故障信号易受到外界的干扰，致使信号的信噪不高，难以准确诊断。

因此，如何准确快速诊断直升机滚动轴承故障，提出安全可靠的预测方法，国内外研究学者进行了广泛的研究［4-11］。前期研究［12］发现，采用小波包对直升机滚动轴承故障信号进行降噪处理，提高信号的信噪比;然后利用局部均值分解法(Local Mean Decomposition，简称LMD)对降噪处理后的振动信号进行分解，得到若干个 PF(Product Function)分量，对这些PF分量进行频谱分析，有效地提取了故障特征。本研究在此基础上，提出了利用径向基函数神经网络(Radial Basis Function Neural Network，简称 RBF)对故障信号进行智能识别的方法，并验证了该方法，以实现准确快速地智能诊断直升机滚动轴承故障。

1 RBF神经网络

RBF神经网络是是一种性能优良的前馈型神经网络，其可以任意精度逼近任意的非线性函数，且具有全局逼近能力。RBF是由输入层、隐藏层及输出层构成，从输入层到隐藏层相当于是把低维空间的数据映射到高维空间;从隐藏层到输出层是对高维空间的数据进行线性分类的过程［13］。RBF 的结构如图1 所示［14］。

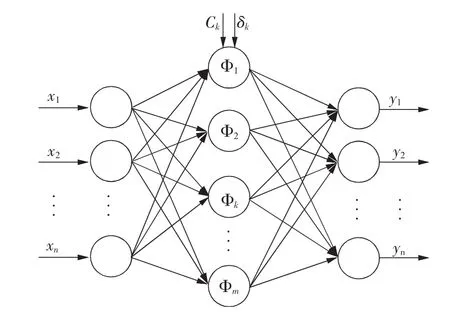
图1 RBF神经网络拓扑结构图Fig.1 The topological structure of RBF neural network

2 基于RBF网络传动系统故障的智能诊断方法

直升机传动系统故障的智能诊断方法主要由3个步骤组成，即振动信号的前处理、特征向量提取和故障识别。在前期研究［12］的基础上，利用RBF对滚动轴承故障故障信号进行智能诊断。具体步骤如图2所示。

首先，利用小波包对样本进行去噪处理，并利用LMD对去噪后的故障信号进行分解，得到具有一定特征值的若干个PF分量［12］;然后，利用这些故障信号对设计好的RBF神经网络进行训练至收敛;最后，用训练至收敛的RBF神经网络对故障信号进行识别。

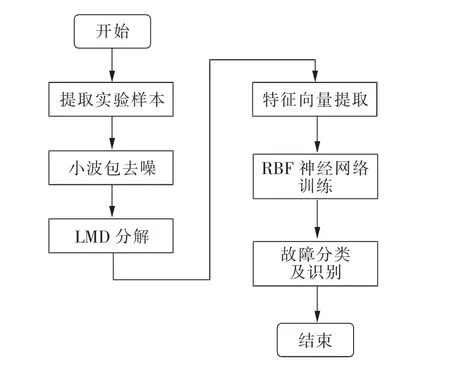
图2 智能诊断实验步骤Fig.2 The process of intelligent diagnosis

3 应用实例

本研究选用美国凯斯西储大学电气工程与计算机科学系轴承实验数据［15］进行实例分析，支承电机传动轴端的6205－2RS SKF深沟球轴承为测试轴承。轴承的钢球直径为8 mm，球组节圆直径为40 mm，钢球数目为9个，接触角为0°。试验台由电动机(1.47 kW)、电器控制装置、测力计、扭矩译码器/传感器等构成。

3.1 故障提取

分别取滚动轴承在正常、内圈故障、外圈故障及滚珠故障四种模式下的振动信号各20组数据，经小波包降噪处理后，再进行LMD分解，得到3个PF分量，并计算各PF分量能量比，结果如表1所示。

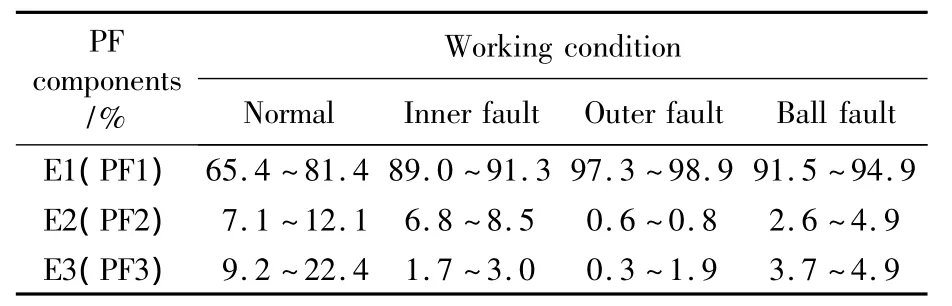
表1 降噪之后得到的PF能量比范围Table 1 The energy ratio range of the PF denoised by wavelet packet

从表1中可知，正常、内圈故障、外圈故障及滚珠故障4种模式下的振动信号经过小波包降噪及LMD分解后得到3种PF分量的能量比值变化趋势各不相同。PF1分量在正常、内圈故障、滚珠故障、外圈故障状态下的能量比逐渐增大，而PF2分量则逐渐减小，PF3分量则在正常、滚珠故障、内圈故障、外圈故障状态下呈减小趋势。从表1结果可以看出，各PF分量的能量比值与不同故障状态下的特征呈一定的关系;因此，PF分量的能量比可以作为神经网络的特征向量。

3.2 神经网络训练

振动信号经过小波包降噪及LMD分解后得到PF分量，计算各分量的能量比，将其作为特征向量，对RBF神经网络进行训练。同时，还对BP(BackPropagation)神经网络进行了训练，以此作为对比。RBF和BP神经网络的建立分别基于MATLAB工具箱中的newrb函数和newff函数，其中newrb函数中的分布密度Spread设置为1.2，newff函数中训练函数为traingdx，其余参数均随机确定。二者训练目标精度均为0.000 1，训练结果如图3所示。

由图3中可以看出，RBF和BP神经网络均训练至收敛。值得一提的是，RBF神经网络只需要25步就能达到0.000 1精度，而BP神经网络则需要238步;因此，相对于BP神经网络，RBF神经网络的训练效果较好，具有一定的优越性。

3.3 故障识别实验及结果

为了考察RBF神经网络对故障的诊断能力，分别取滚动轴承在正常、内圈故障、外圈故障及滚珠故障4种模式下的振动信号各5组未参与训练的数据进行故障识别验证。这些数据经小波包降噪和LMD分解得到相应的特征向量，分别用训练好的RBF和BP神经网络，并进行分类识别，结果如表2所示。

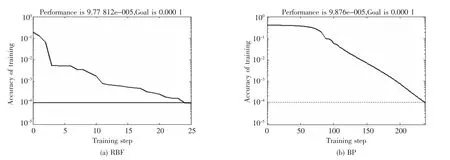
图3 神经网络训练误差Fig.3 The training errors of neural network

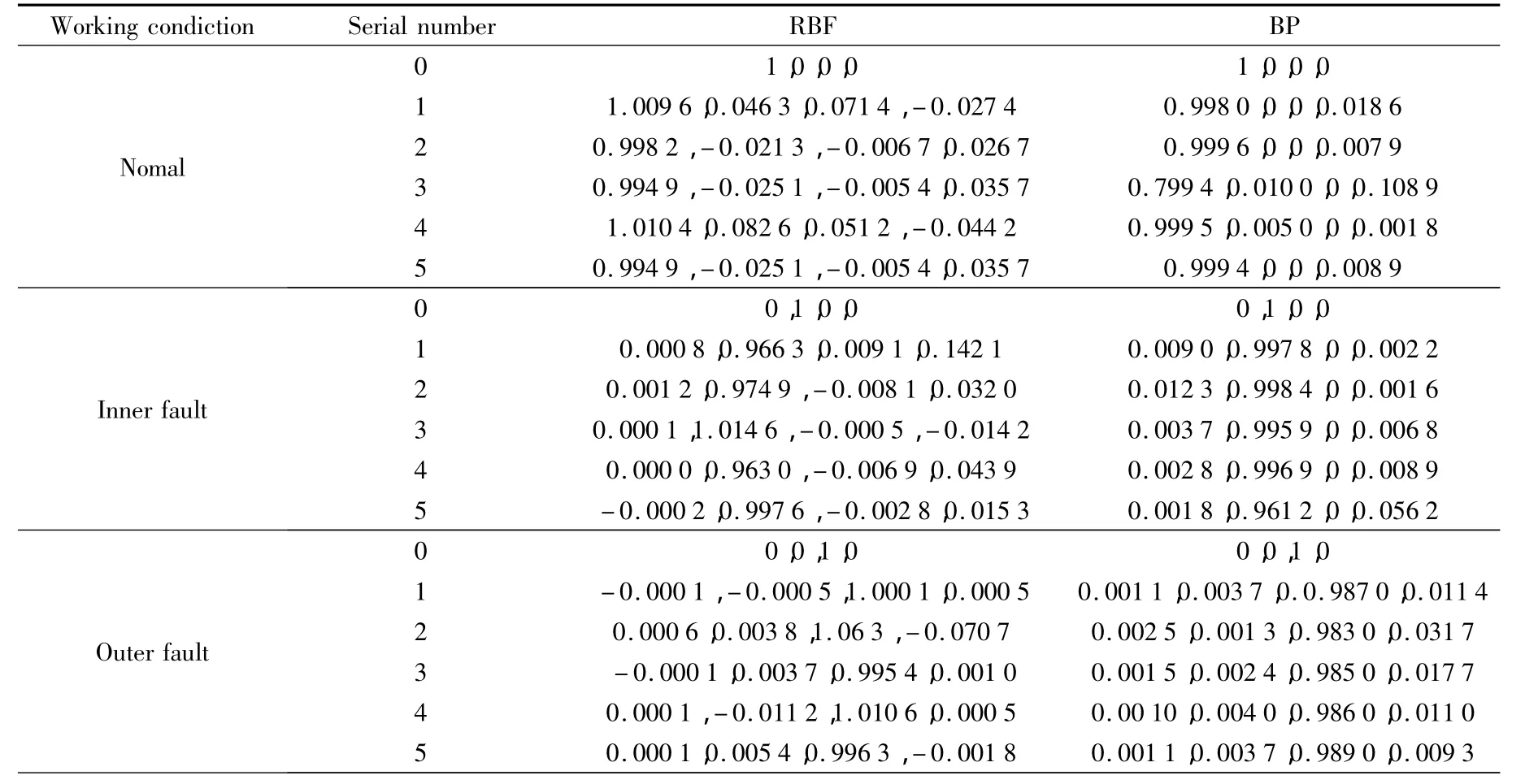
表2 神经网络输出结果Table 2 The output results of neural network

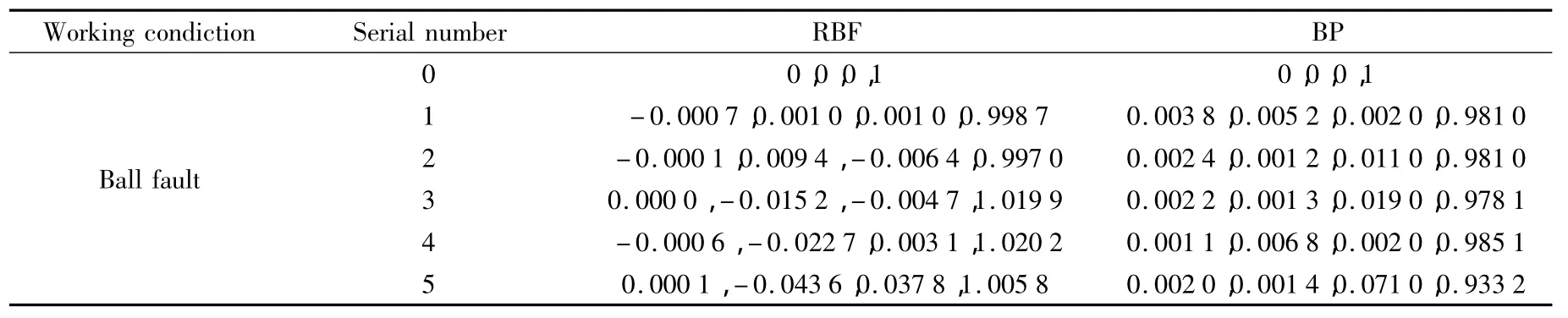
续表2

表2中每种状态下第0组数据为其采用的矩阵编码。如果选取判断区间为(0.2，0.8)，从表2中可以看出，RBF神经网络识别率达到100%;而BP神经网络正常状态下第3组实际输出数据为［0.7994，0.0100，0，0.1089］，介于(0.2，0.8)区间，故认为识别失败。因此，RBF神经网络比BP神经网络更能准确地对故障类型进行识别。

4 结论

1)通过小波包对实验数据进行降噪处理，利用LMD方法分解，并提取滚动轴承故障特征;然后，用故障样本对设计好的RBF神经网络进行训练，最后利用训练好的RBF网络进行滚动轴承故障的智能诊断。

2)实验结果表明:故障识别率达到了100%，表明该方法能够有效地对滚动轴承故障进行分类识别。

［1］Samuel P D，Pines D J.Constrained adaptive lifting and the CAL4 metric for helicopter transmission diagnostics［J］.Journal of Sound and Vibration，2009，319(1 －2):698 －718.

［2］Bayissa W L，Haritos N，Thelandersson S.Vibration-based structural damage identification using wavelet transform［J］.Mechanical Systems and Signal Processing，2008，22(5):1194 －1215.

［3］Samuel P D，Pines D J.A review of vibration-based techniques for helicopter transmission diagnostics［J］.Journal of Sound and Vibration，2005，282(1 －2):475 －508.

［4］Hardman W，Hess A，Shaffer J.SH-60 helicopter integrated diagnostic system program-diagnostic and prognostic developmentexperience［J］. IEEE Aerospace Conference Proceedings，Snowmass，1999:473 －491.

［5］Michael A，Andy H，Harley R.Implementing HUMS in the military operational environment［R］.Annual Forum Proceedings American Helicopter Society 2001，Fort Worth，2001:1822 －1830.

［6］Green A J.The development of engine health monitoring for gas turbine engine health and life management［R］.AIAA 98 －3544，19981.

［7］张新锋，赵彦，施浒立.机械结构系统模糊可靠度数值计算方法［J］.中国机械工程，2009，3:25－28.

［8］李瑰贤，于广滨，马良.基于模糊故障树直升机起落架液压系统的故障诊断方法研究［J］.机床与液压，2007，5:19－21.

［9］Ambarisha V，Parker R.Suppression of planet mode response in planetary gear dynamics through mesh phasing［J］.Journal of Vibration and Acoustics，2006，128(2):133 －142.

［10］Combet F，Zimroz R.A new method for the estimation of the instantaneous speed relative fluctuation in a vibration signal based on the short time scale transform［J］.Mechanical Systems and Signal Processing，2009，23(4):1382－1397.

［11］肖露，熊邦书，莫燕，等.基于分段幂函数的LMD方法及其在轴承故障诊断中的应用［J］.失效分析与预防，2013，8(2):88－93.

［12］孙伟，熊邦书，黄建萍，等.小波包降噪与LMD相结合的滚动轴承故障诊断方法［J］.振动与冲击，2012，31(18):153－156.

［13］雷素娟.一种改进的RBF神经网络及其在股市中的应用［D］.厦门:华侨大学，2009:24－34.

［14］孟艳，潘宏侠.PSO聚类和梯度算法结合RBF神经网络优化［J］.自动化仪表，2011，32(2):6 －8.

［15］Case Western Reserve University Bearing Data Center Website［OL］.http://www.eecs.case.edu/laboratory/bearing/.2011－5－03.