基于多指标正交实验的涡流探头优化设计
祝忆春,杨琳瑜,邱玉兰
(1.中国联合网络通信有限公司江西省分公司,南昌 330096;2.无损检测技术教育部重点实验室(南昌航空大学),南昌 330063)
0 引言
涡流检测(Eddy Current Testing,ET)是基于电磁感应原理揭示导电材料表面和近表面缺陷的无损检测方法[1]。当载有交变电流的检测线圈靠近被测导体试件时,由于线圈磁场的作用,试件中产生感应涡流,而涡流的存在又影响检测线圈周围的磁场分布,线圈的阻抗也就随之变化[1]。涡流探头即检测线圈是拾取涡流场强度及分布变化的传感器。被测金属工件的材质、尺寸、表面状态、激励信号的频率、线圈与被测表面的距离、线圈参数等均会影响涡流场的强度及分布,改变其中任何一个参数都会引起涡流场的变化,涡流场反作用于检测线圈从而使线圈的阻抗发生变化。涡流检测探头是用来连接被测金属材料和涡流测试仪器的敏感元件,是将被测金属材料特性、缺陷等相关信息转变为阻抗变化输出的器件[2],因此涡流检仪器的质量、检测系统的灵敏度直接取决于探头性能的好坏。当今常用的涡流检测探头主要包括激励线圈、检测线圈、磁芯、支架以及外壳磁饱和器几个部分。涡流探头设计的常用方法为实验法、解析法和数值法[3]。解析法是基于电磁理论,推导线圈的阻抗的解析解,从而确定线圈所配置的具体参数。数值法是基于快速增长的计算机技术,通过数值建模求解有关线圈响应的数值解从而实现对涡流探头性能的模拟。3种设计方法各有优越性和局限性。近年来,涡流探头的设计理论逐步发展,例如张玉华等研究了基于场-路耦合模型的涡流探头设计,Buvat F等[4]研究了含铁氧体磁芯的电涡流传感器线圈阻抗理论模型和数值计算。杜平安等[5]采用三维有限元模型对涡流传感器进行仿真和设计。但理论模拟毕竟不能代替实际,理论模拟确定的参数只能作为参考,实验法对于探头的改进仍起最重要作用,是涡流探头设计中不可替代的方法。实验法必须借助实践经验及大量的实验进行反复的修正、改进,从而确定较为适合的探头参数。鉴于涡流探头性能的影响因素较多,每个因素对探头不同性能的影响各不相同,如何以最少的实验试验次数,获得尽量多的有用信息,并且能方便的分析试验结果是采用实验方法进行涡流探头设计需要考虑的问题。而正交设计正是一种多因素、多水平、高效、经济的实验方法[6]。
本研究以用于金属表面无损探伤的点式探头为例,选取影响探头性能的几个主要因素,以多指标正交实验为基础,通过试验据数据分析,综合决定各因素主次及最优水平组合,以得到性能优良的涡流检测探头。
1 实验设计
点式涡流探头是通以正弦电流的线圈,在实际操作中,为提高检测灵敏度并有效分离各种影响因素,应选择合适的检测频率。频率过小穿透深度增加,但“直径效应”方向与“裂纹效应”方向的夹角很小,甚至无法区分[7]。当频率比过大趋肤效应相当明显,检测绝对灵敏度已经显著下降,故要依据检测目的和对象选择不同频率[2]。线圈结构尺寸对涡流场的影响表现为:线圈外径影响周围磁场的分布,线圈近场磁感应强度随着外径减小而增加,但远处延线圈轴线方向磁感应强度衰减快,表现为渗透深度减小、检测灵敏度高、线性范围变小[8]。线圈内径对磁感应强度的影响不大;线圈的轴向厚度与灵敏度呈反比。线圈匝数对探头的影响需综合考虑。一方面,线圈的匝数影响线圈电感量的大小,匝数减少使线圈阻抗减少,激励能量增加,有利于灵敏度的提高;另一方面,激励线圈匝数减少降低了线圈与试件之间的藕合程度,不利于提高灵敏度。感应线圈中插入磁芯可以增大绕组间的电磁耦合、限定磁场范围,能增强线圈电感,减少线圈的分布电容,有助于提高检测灵敏度[9]。综上所述,线圈的检测频率f、线圈的外径D、线圈匝数n、磁芯直径d都是探头设计中的重要参数。
正交实验设计法是研究与处理多因素实验的一种科学方法。是依据数理统计的原理,应用一种标准化了的“正交表”在大量的试验点中科学地挑选合适并具有代表性的试验点,合理安排实验的一种方法。它具有整齐可比性和均衡分散性,可以减少实验次数,大大提高实验效率[6]。本次实验选取线圈检测频率f、线圈的外径D、线圈匝数n、磁芯直径d 4个因素。结合以往实验结果,因素水平选取如表1所示。采用L9(34)正交表安排试验,实验方案如表2所示。

表1 因素水平表Table 1 Factor combination

表2 实验方案及结果Table 2 Experiment scheme and record
探头连接检测系统如图1所示,涡流探头采用绝对式探头,具备产生激励信号及拾取检测信号2个功能,拾取的交流信号经相敏检波、放大电路调理后经A/D转换送至计算机。待检试块预制了4个模拟裂纹缺陷的刻槽、3个模拟腐蚀坑缺陷的平底孔,尺寸数据如图2所示。
2 试验结果及分析
按照表2设计方案制作了9个探头,实验时探头由左至右探测,输出信号如图3所示。由图可见,该系统能有效检测出缺陷,且输出信号能有效区分裂纹型缺陷和孔形缺陷。缺陷深度与输出信号幅值有关,因此取缺陷处信号幅值电压作为定量缺陷深度的标准。试验指标选择反映系统静态特性的主要指标——灵敏度和线性度。

图1 检测系统Fig.1 Detection system

图2 检测试块示意图Fig.2 Schematic drawing of detection specimens
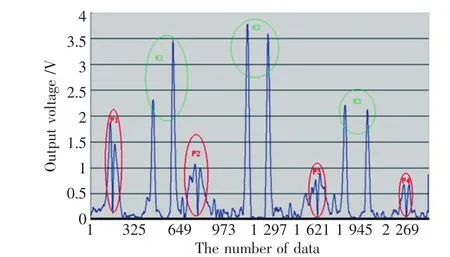
图3 1#探头输出信号图Fig.3 Signal wave of probe 1#
1#探头实验结果如表3所示,静态校准曲线如图4所示。探头校准曲线经最小二乘法拟合,得拟合直线方程y=0.036+0.9x,则该探头的检测灵敏度即为拟合直线斜率0.9 V/mm。探头校准曲线与拟合直线间最大偏差与满量程输出值的百分比为线性度,则探头1的线性度为9.5%。依次进行表2的9次试验,结果见表4。在两项指标中,灵敏度越大越好,线性度越小越好。

表3 1#探头试验结果Table 3 Scheme and record of probe 1#
数据分析采用综合评分法判断探头性能的优劣,是一种将多指标按着一定的规则转换为单指标的方法。综合评分判据为:每项指标的最优值定为满分10分,最差值定为1分,其他介于两者之间的数值则依据该指标值与最优值的差异按比例计分,综合评分公式如式(1),保证其值在1~10。例如对于灵敏度指标,第4号探头最高为1.1,计10分;第7号探头最低为0.47,计1分。对于线性度指标,第5号探头误差最小为8.9%,计10分;第9号探头误差最大为14.2%,计1分。其他介于最优和最差之间的指标值的综合评分按公式1计算得分。

图4 1#探头静态校准曲线Fig.4 Statical calibration curve of detector No.1

综合比较各种指标的重要性及其实测值,对于实际应用,灵敏度指标的重要性高于线性度指标;因此,灵敏度加权系数定为2,线性度加权系数定为1,对每号试验结果评定出一个综合分数,综合评分=2×灵敏度评分+1×线性度评分,以此分数作为单指标进行统计分析。依据每号试验的综合评分,极差分析如表5所示,其中Kj1、Kj2、Kj3分别为因素水平1、水平2、水平3的试验之和;kj1、kj2、kj3分别为因素水平 1、水平 2、水平 3 的试验平均值;Rj为极差。
由表4、表5可知,9次试验中1号试验综合评分最高,即试验条件为f1n1d1D1,根据极差分析表 5,因素主次顺序为 f、n、d、D,其中因素 n、d的作用基本相当,较佳参数方案是f1n1d2D2。
由于f1n1d2D2不在9次试验范围之列,因此选择这一参数重新制作线圈,重做以上实验,实验结果为:灵敏度1.05,线性度9.1%,综合比较前9次试验,这一参数方案具有较高的灵敏度和较好的线性度,综合性能优于此前试验参数。
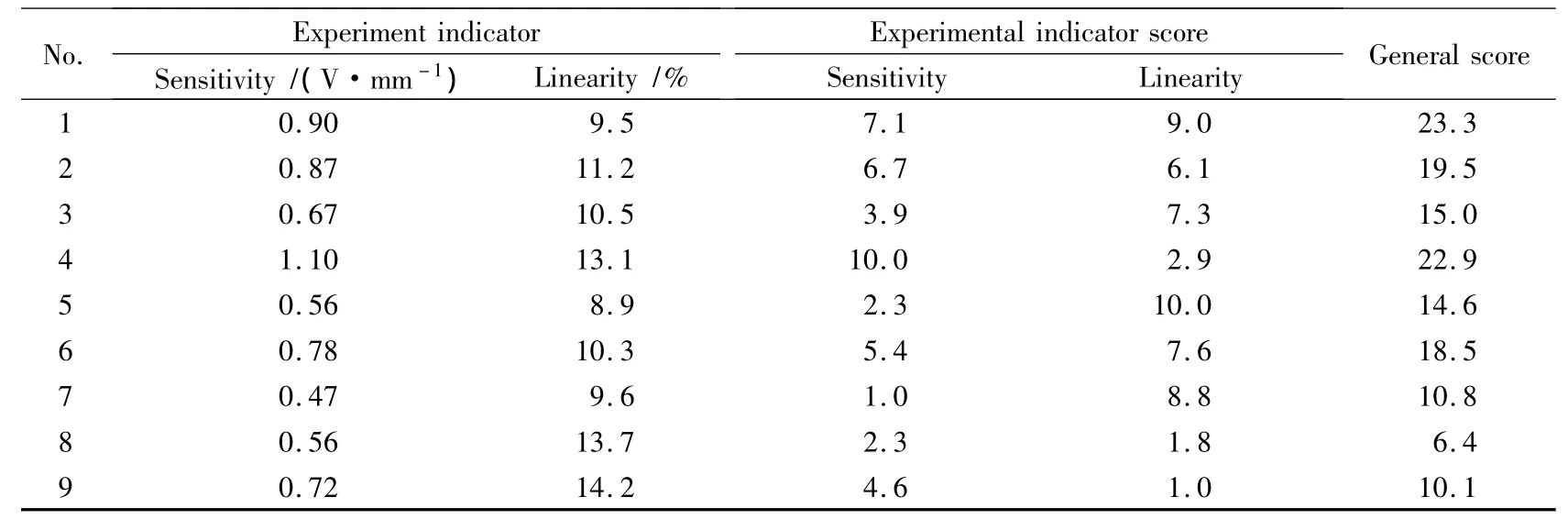
表4 综合评分法结果数据表Table 4 Results of comprehensive evaluation
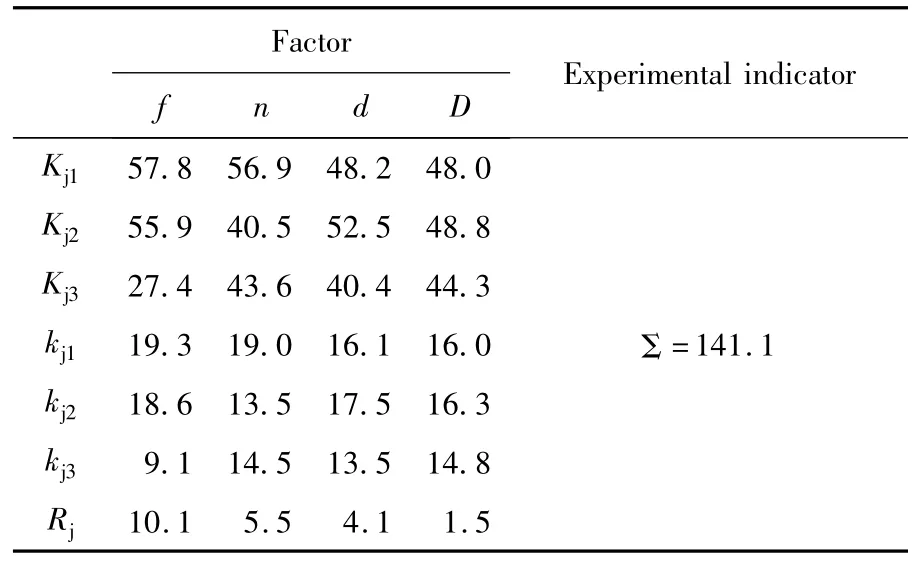
表5 极差分析表Table 5 Range analysis table
由表5可知,极差反映各因素对综合性能的影响,因此4个影响因素中,因素f的影响最大;因素n、d次之,且作用程度相似;因素D影响最小,且作用远低于前3个影响因素。各项因素的水平参数评分表明,因素f中水平1、2,综合性能相似,优于水平3;因素n随着水平的增加,探头性能降低;因素d也显示水平的增加将降低探头性能。
3 结论
1)运用正交实验设计方法确定的各因素对探头综合性能贡献率的主次顺序为:检测频率f,探头的线圈匝数n,磁芯尺寸D,线圈的外径d。
2)实验选取4个因素3个水平,经9次实验得到综合性能最高的参数配置,即频率20 kHz、匝数20匝、磁芯直径2 mm、外径4 mm的探头参数组合为最佳组合。
3)检测频率为20~50 kHz,综合性能相差不大,频率过高将降低探头性能;线圈匝数增加,探头性能降低;磁芯直径过大将降低探头性能。据此可以进一步细化各水平范围,增加水平数量,以期找到最优参数组合。
[1]任吉林,林俊明.电磁无损检测[M].北京:科学出版社,2008:65-85.
[2]单成祥.传感器的理论与设计基础及其应用[M].北京:国防工业出版社,1999:56-58.
[3]美国无损检测学会.美国无损检测手册(电磁卷)[M].《美国无损检测手册》译审委员会译.上海世界图书出版公司,1999:78-82.
[4]Buvat F,Pichenot G,Premel D,et al.Eddy-current modeling of ferrite-cored probes[C].Proceedings of AIP Conference,2005,760:463-470.
[5]Yu Y T,Du P A.Research on the correlation between measured material properties and output of eddy current sensor[J].IEEE International Conference on Industrial Technology,HongKong,2005:428-431.
[6]Jeff Wu C F,Hamade M.实验设计与分析及参数优化[M].张润楚,郑海涛,兰燕,等译.北京:中国统计出版社,2003:25-29.
[7]Huang H,Endo H,Uchimoto T,et al.Eddy current testing and sizing of deep cracks in a thick structure[J].Review of Quantitative Nondestructive Evaluation,2004,700(23):659-666.
[8]Li S,Huang S L,Zhao W.Development of differential probes in pulsed eddy current testing for noise suppression[J].Sensors and Actuators,2007,135(2):675 -679.
[9]Theodoulidis T P,Krezis E E.Impedance evaluation of rectangular coils for eddy current testing of planar media[J].NDT & E International,2002,35(6):407-414.

