关于Diophantine方程x3－1＝Dy2（D＝p，2p）

杜先存

（红河学院 教师教育学院，云南 蒙自661199）

方程x3±1＝Dy2（D是无平方因子的正整数）是一类重要的Diophantine方程，其整数解已有不少人研究过。柯召和孙琦证明了当D不含3或6k＋1型的素因子时，方程x3±1＝Dy2无整数解［1］。但当D含6k＋1型的素因子时，方程的求解较为困难。段明辉给出了方程x3＋1＝57y2的全部整数解［2］。杜先存等给出了D为3（8m＋k）（8m＋k＋1）＋1（m，k∈N，k≤7）型的奇素数时，方程x3－1＝Dy2无正整数解的两个充分条件［3］。文献［4］给出了方程x3－1＝Dy2无正整数解的3个充分条件。文献［5］给出了方程x3±1＝2py2无正整数解的两个充分条件。黄寿生证明了p为48s2＋1（s∈Z＋）型素数时，方程x3－1＝2py2无正整数解［6］。

本文将主要讨论p为6k＋1型奇素数，且D＝p，2p时，Diophantine方程x3－1＝Dy2解的情况。

1 若干引理

引理1［4］若p＝3n（n＋1）＋1（n∈N），则px2－3y2＝1（1）的最小解为（2，2n＋1）。

引理2［7］设ɑ＞1，（ɑ，b）∈N2，ɑb不是完全平方数，如果有解（x，y）∈N2，设是方程ɑx2－by2＝1（x，y∈Z）的基本解，则ɑx2－by2＝1的任一组解可以表示为

引理3［8］设p是奇素数，则方程组x－1＝3pu2，x2＋x＋1＝3v2仅当p＝7时有非零整数解x＝22，u＝1，v＝13。

引理4［8］设p是奇素数，则方程组x－1＝6pu2，x2＋x＋1＝3v2仅当p＝13时有非零整数解x＝157，u＝2，v＝181。

2 主要定理

定理1 设奇素数p＝3n（n＋1）＋1≡1，5（mod 8）（n∈N），若存在形如8k－1，8k－3型的素数q使得q｜（2n＋1），则Diophantine方程

无正整数解。

定理2 设奇素数p＝3n（n＋1）＋1≡1，7（mod 8）（n∈N），若存在形如8k－1，8k＋3型的素数q使得q｜（2n＋1），则Diophantine方程

无正整数解。

3 定理的证明

3.1 定理1的证明

证明 因为gcd（x－1，x2＋x＋1）＝1或3，故给出以下4种分解：

情形Ⅰ：x－1＝pu2，x2＋x＋1＝v2，y＝uv；

情形Ⅱ：x－1＝3pu2，x2＋x＋1＝3v2，y＝3uv；

情形Ⅲ：x－1＝u2，x2＋x＋1＝pv2，y＝uv；

情形Ⅳ：x－1＝3u2，x2＋x＋1＝3pv2，y＝3uv。

对于情形Ⅰ，由x2＋x＋1＝v2，得x＝0或－1，代入x－1＝pu2均不成立，故情形Ⅰ无正整数解。

对于情形Ⅱ，因p＝3n（n＋1）＋1≡1，5（mod 8）为奇素数，则p≠7，故由引理3知，情形Ⅱ无正整数解。

对于情形Ⅲ，由x－1＝u2，得x－1≡0，1，4（mod 8），得x＝u2＋1≡1，2，5（mod 8），则x2＋x＋1≡3，7（mod 8）。

由x2＋x＋1＝pv2知v为奇数，故v2≡1（mod 8），而p≡1，5（mod 8），故pv2≡1，5（mod 8），则有3，7≡x2＋x＋1＝pv2≡1，5（mod 8），矛盾。故情形Ⅲ无正整数解。

对于情形Ⅳ，将x－1＝3u2代入x2＋x＋1＝3pv2，整理得

则（2v，2u2＋1）是方程（1）的一组解。因为p＝3n（n＋1）＋1，则由引理1，得（2，2n＋1）是方程（1）的最小解。

由引理2知，从（4）可得

由式（5）可得2u2＋1≡0（mod（2n＋1）），因为q｜（2n＋1），所以2u2＋1≡0（modq），因此2u2≡－1（modq），即（2u）2≡－2（modq），则模q的勒让德符号

又由题意知，q≡5，7（mod 8），故矛盾。由此可知，情形Ⅳ无正整数解。

综上有，方程（2）在题设条件下无正整数解。

3.2 定理2的证明

证明 因为gcd（x－1，x2＋x＋1）＝1或3，方程（3）给出以下4种分解：

情形Ⅰ：x－1＝2pu2，x2＋x＋1＝v2，y＝uv；

情形Ⅱ：x－1＝6pu2，x2＋x＋1＝3v2，y＝3uv；

情形Ⅲ：x－1＝2u2，x2＋x＋1＝pv2，y＝uv；

情形Ⅳ：x－1＝6u2，x2＋x＋1＝3pv2，y＝3uv。

对于情形Ⅰ，由x2＋x＋1＝v2，得x＝0或－1，均不适合x－1＝2pu2，故情形Ⅰ无正整数解。

对于情形Ⅱ，因p＝3n（n＋1）＋1≡1，7（mod 8）为奇素数，则p≠13，故由引理4知，情形Ⅱ无正整数解。

对于情形Ⅲ，由x－1＝2u2，得x＝2u2＋1≡1，3（mod 8），则x2＋x＋1≡3，5（mod 8）。

由x2＋x＋1＝pv2知v为奇数，故v2≡1（mod 8），而p≡1，7（mod 8），故pv2≡1，7（mod 8），矛盾。故情形Ⅲ无正整数解。

对于情形Ⅳ，将x－1＝6u2代入x2＋x＋1＝3pv2，整理得

则（2v，4u2＋1）是方程（1）的一组解。因为p＝3n（n＋1）＋1，则由引理1，得（2，2n＋1）是方程（1）的最小解。

由引理2知，从（7）可得

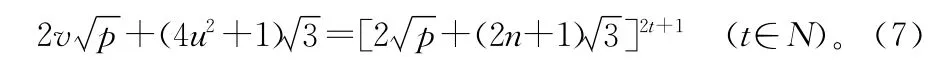
由（7）可得4u2＋1≡0（mod（2n＋1）），因为q｜（2n＋1），所以4u2＋1≡0（modq），因此（2u2）≡－1（modq），故模q的勒让德符号

又由题意知，q≡3，7（mod 8），故矛盾。由此可知，情形Ⅳ无正整数解。

综上有，方程（3）在题设条件下无正整数解。

［1］柯召，孙琦.关于丢番图方程x3±1＝Dy2［J］.中国科学，1981，24（12）：1453－1457.

［2］段明辉.关于丢番图方程x3＋1＝57y2［J］.重庆师范大学学报，2010，27（3）：41－43.

［3］杜先存，李玉龙，赵金娥.关于不定方程x3－1＝Dy2［J］.四川理工学院学报，2012，25（4）：79－80.

［4］杜先存，史家银，赵金娥.关于不定方程x3－1＝Py2［J］.西南民族大学学报：自然科学版，2012，38（5）：748－751.

［5］杜先存，赵东晋，赵金娥.关于不定方程x3±1＝2Py2［J］.曲阜师范大学学报：自然科学版，2013，39（1）：42－43.

［6］黄寿生.关于指数 Diophantine方程x3－1＝2Py2［J］.数学研究与评论，2007，27（3）：664－666.

［7］夏圣亭.不定方程浅说［M］.天津：天津人民出版社，1980：97－98.

［8］张同斌，潘家宇.关于丢番图方程x±1＝3Dy12，x2x±1＝3y22［J］.河南教育学院学报：自然科学版，1999，8（3）：1－3.