国外关于要素再配置效应的度量方法述评

栾大鹏，王士海

（1.中央财经大学 国民经济学系，北京100081；2.山东农业大学 农林经济管理系，山东 泰安271000）

上世纪90年代以来，围绕我国要素再配置效应问题所展开的研究愈渐增多。然而对于要素再配置效应是否在我国存在，以及其在现实中的表现是否明显两个议题，到目前尚未形成统一定论。这其中的主要原因在于：在测度我国要素再配置效应时，不同学者往往采取了不同的度量方法。基于此，本文重点对国外关于要素再配置效应的度量方法及其各自的适用条件进行了介绍和说明，以期为国内学者今后开展相关研究提供方法上的参考和借鉴。

1 要素再配置的内涵和存在前提

要素再配置效应理论是由Chenry，Feder和Syrquin通过对多国经济增长间的比较建立起来的［1－3］。在基本内涵上该理论认为，当存在 “结构红利”的时候，由产业结构等结构性变动所引致的生产要素（资本和劳动）在国家、地区、产业或部门间的再配置，会改变其各自的产出效率水平，继而也就会对经济的总产出产生重要影响，并且要素再配置是生产率提高和总产出增长的重要源泉之一。

虽然从理论上来看，要素再配置效应在现实中的存在需要以在国家、产业或部门间的不同要素产出效率，即“结构红利”的存在作为基本条件，但是我们同时又能够发现，要素产出效率在国家、产业或部门间的不同，在现实中往往又表现为常态。因为诸如二元经济结构、要素流动所面临的成本限制、政府部门对要素配置的干预，以及不完善的市场经济体制等等一系列影响市场有效配置要素资源的因素，都会导致国家、产业或部门间在要素产出效率上的不同。如Feder就认为，分割的市场对于要素充分流动的限制、政府部门对于投资的过度干预，以及持续不断的技术变革等因素，都是阻碍生产要素有效流动的现实因素，继而也会使得国家、产业或部门间的要素产出效率在现实中的表现并不相同［2］。Syrquin也认为，尽管市场力量倾向于改进总体的资源配置结构，并使整体的经济系统向更加均衡化的方向调整，但是，系统的稳定性和调整上的高额成本无疑减弱了这种力量。同时，这种力量还可能会在诸如外部事件、非平衡的生产率增长，甚至是政府政策等因素的影响下而被削弱［3］。

2 要素再配置效应的度量方法

从近些年来看，国外关于要素再配置效应的度量方法，广为接受和普遍被采用的主要包括三种：转移－份额法（Shift－share analysis）、索洛余值分解法和全要素生产率差额法。而且应该说，虽然在具体的模型设计和分析视角的选择上，三种方法之间还存在着很大的不同，但是从根源上来讲，对于这三种方法而言，都是以要素产出效率在国家、地区、产业或部门间存在差异为基础而建立起来的。此外，尽管转移－份额法、索洛余值分解法重点分析的是产业间的要素再配置效应，全要素生产率差额法重点分析的是部门间的要素再配置效应，但是对于其中任何一种方法来讲，无论是分析国家和地区间的要素再配置效应问题，还是分析产业或部门间的要素再配置效应问题，同样都是能够适用的。

2.1 转移－份额法

转移－份额法也称之为偏离－份额法，最早是由Fabricant在分析劳动力人口在产业间的转移和流动对于其自身产出效率水平所产生的效应时提出［4］，并经由 Massell基于新古典增长模型进行扩展后［5］，建立起的一套考察产业间结构变动所引起的资本和劳动两个生产要素流动对于两个要素自身产出效率水平如何形成影响以及形成何种影响的方法。具体而言，首先，它将要素（平均）生产率的增长解释为全部是由技术变革所引起的，而在这样的处理方式下，就可以把技术变革对于经济增长所产生的影响完全归结于是通过引致生产要素的产出效率发生了变化，由此不仅增强了理论上的说服力，也有效地降低了实证分析上的难度；其次，关于技术变革对于要素产出效率水平所产生的影响，又可分解为产业间要素再配置所带来的贡献和产业内要素产出效率变化所带来的贡献两个部分；最后，关于产业间要素再配置所带来的贡献，则又可进一步细分为要素的静态转移效应和要素的动态转移效应两个部分。

从模型的设定上来看，在下述式（1）中，如果g代表某一时期内要素（资本或劳动）生产率的总体增长率，G代表该种要素在三次产业内的平均生产率水平，下标0代表初始时期，t代表期末，i代表（三次）产业，i＝1，2，3，Si代表产业i内该种要素投入量占该要素在三次产业投入总量的比重。那么转移－份额法的理论模型可具体表述为

在上式中，左边起前两项分别表示在t时期内要素生产率的总体增长率；右边第一项（自左边数第三项）表示要素的静态转移效应，它反映了在各产业内要素生产率水平保持不变的情况下，要素从低生产率水平的产业向高生产率水平的产业转移时引致要素生产率增长的大小；右边第二项表示要素的动态转移效应，它反映了在各产业内要素生产率水平发生变化的情况下，要素从低生产率水平的产业向高生产率水平的产业转移时引致要素生产率增长的大小；右边第三项表示产业内的增长效应，它反映了在不考虑产业结构变动的情况下各产业内要素生产率增长的加权平均值。Massell认为，经过这样的分解后，式（1）右边的前两项之和，事实上也就反映了由产业结构变动所引起的要素流动，对于各要素自身产出效率水平所形成的总体影响，以及对于整体经济增长所形成的再配置效应［5］。

也就是说，虽然转移－份额法的提出和建立，主要是为了分析产业结构变动对于要素产出效率所形成的影响，但是由于其将这种影响进一步地拆分成为产业间的结构效应和产业内的增长效应两个部分，因此通过使用该方法，也能够测度出要素再配置对于要素产出效率所形成的具体影响。而且从求解的整个过程来看，该方法对于数据的要求并不十分苛刻，求解起来也相对比较容易。也正是因为如此，国内外学者在后来分析某些国家或地区要素再配置效应问题时，很多采用了该种方法。

2.2 索洛余值分解法

2.2.1 索洛余值法

在介绍索洛余值分解法之前，有必要先对索洛余值法进行一下描述。该方法由美国经济学家罗伯特·索洛（Robert M.Solow，1957）提出［6］。经过一系列的推导，索洛证明了，在仅投入资本和劳动两种生产要素，以及在技术进步满足希克斯中性的前提下，技术进步引致总产出水平的变动率在数值上就等于产出增长率中扣除资本和劳动两者贡献后的余额。

从具体推导过程来看，首先，如果Q代表经济的总产出水平，K和L分别代表资本和劳动要素的投入量，时间趋势t代表技术进步水平，那么总生产函数可表述为如下形式：

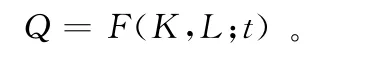
其次，引入技术进步满足希克斯中性的假设，即其不仅独立地影响总产出，而且也不会改变工资和利润两者在总产出中所占的相对份额，于是上式就可具体表述为：

其中，式中的A（t）代表具有希克斯中性的技术进步。进一步而言，对该式左右两边分别关于时间t求导，并除以总产出水平Q以后，就可以得到：

应该说，索洛余值法避开了对于生产函数具体形式的讨论，而更多关注的是函数的相关性质，这使得基于上述推导所得到的关于技术进步对于经济增长贡献的度量方法有了广泛的适用性。然而需要注意的是，该方法也存在着先天的缺陷和不足。具体而言，在索洛模型中，技术进步对于经济增长的贡献被界定为产出增长中扣除资本和劳动两者贡献后的 “余值”，因此可以说，该“余值”实际上涵盖了任何可能导致总生产函数发生变动的因素。然而在现实中，除资本和劳动两种要素的投入之外，并非任何可能导致总产出增长的因素都可归结为技术进步。这也就是说，由于索洛余值中所包含的因素过于宽泛，故而也就不能准确地反映出现实中技术进步对于经济增长所形成的实际影响。而对于中国这样一个处于经济转型阶段的发展中国家来说，因为现实中影响经济增长的因素着实有很多，所以情况就更是如此。

2.2.2 索洛余值分解法

鉴于索洛余值中所涵盖的内容过于宽泛，因此对其细化和分解，进而使索洛余值更加贴近现实中技术进步对于经济增长所形成的影响，也就显得十分必要。索洛余值分解法则正是在此种背景下得以产生。具体而言，该方法就是在索洛所展开的传统分析的基础上，将索洛余值中包含的一系列非技术因素对于经济增长所形成的影响逐个地发掘并从中分解出来。

首先，在考虑影响经济增长的其他非技术因素的情况下，将索洛的总生产函数扩展为如下形式：

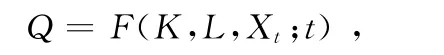
在该式中，Q，K和L分别与其各自在索洛模型中所代表的基本含义相同。而Xt＝ （x1t，x2t，…，xNt），则代表影响经济增长的一系列其他非技术因素。

其次，对于该式而言，在假设技术进步满足希克斯中性的基础上，按照索洛余值法所给出的推导逻辑，可经过逐步地推导得到：

但是值得注意的是，这里的技术进步A与其在索洛模型中所包含的内容已经出现了不同，因为相对于索洛模型经进一步分解，很多影响经济增长的非技术因素从索洛余值中被分离了出来。而且可以发现，与之前索洛余值中的技术进步相比，此时的技术进步A在范围上无疑得到了一定的缩小，当然也更加贴近了现实中的（狭义）技术进步。更为重要的是，将索洛余值进行分解之后，对上述各种非技术因素对于经济增长所形成的具体影响展开实证考察也在事实上成为了可能。我们知道，索洛最初所设定的总生产函数，满足CD（柯布－道格拉斯）生产函数所具有的相关性质，而这也同样适用于基于索洛余值分解法所得到的总生产函数。因此在开展实证分析时，就可具体以索洛余值的这种分解为基础，建立扩展性的C－D生产函数模型，继而来考察系列非技术因素分别对于经济总产出所形成的实际影响。如Chenry就率先使用过该方法，并将产业间的要素再配置等一系列影响经济增长的非技术因素相继加入到了传统的新古典增长模型之中，在多国之间的比较中对这些因素对于各国经济增长所形成的影响展开了实证考察［1］。而且从国内外相关文献来看，自进入本世纪以来，这种方法逐渐被采用得愈加广泛。

2.3 全要素生产率差额法

该方法最早由Syrquin提出，在他看来，总产出和要素生产率水平的增长可以在3组相互作用的供给要素的变化中得到说明：（1）主要投入的变化，即资本积累和就业扩大；（2）部门内要素利用效率的改善，即各部门全要素生产率的增长；（3）各部门之间的资源再配置。这也就意味着，对于要素再配置效应而言，在数值上就等于经济总体全要素生产率的增长率减去各部门全要素生产率的增长率加权平均值后的余额［3］。

具体来说，对于各经济部门的总产出增长而言，如果以一个具有规模收益不变特征和技术进步满足希克斯中性的C－D生产函数来进行刻画的话，就可将其表述为如下形式：

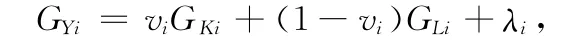
其中，i代表各经济部门，GYi，GKi，GLi，λi分别代表部门i内的总产出水平Yi，资本投入量Ki，劳动投入量Li和全要素生产率的增长率，vi代表资本的产出份额。

不难发现，在上式的基础上，我们可将经济的总产出水平表述为：

其中，Y＝ ∑Yi，代表经济的总产出水平，ρi＝Yi／∑Yi＝Yi／Y，代表部门i内的总产出在经济总产出中所占的份额，其他变量所代表的含义与前述相关模型中所代表的含义相同。

另一方面，从各部门加总的角度来看，经济的总增长函数还可表述为如下形式：

其中，K＝∑Ki，L＝∑Li，v＝∑ρivi，λ代表经济总体全要素生产率的增长率。

在Syrquin看来，经济总体全要素生产率的增长，来自于两个方面的贡献：一是各经济部门全要素生产率的增长；二是要素转移所带来的要素配置和产出效率的改善。因此，如果定义要素再配置效应为TRE，那么综合上面的推导，我们就可以得到：

而且，从该式中我们可以看到，对于要素再配置效应而言，其由两部分构成：资本再配置效应和劳动再配置效应。与此同时，如果我们将代入上式，那么就可以进一步得到：

其中，MPKi和MPLi分别代表部门i内资本和劳动的边际产出水平，Ki和Li分别代表部门i内资本和劳动投入的绝对变动量。与此同时，该式中的各项及其各自所代表的含义表明，当某一部门内要素的边际产出水平大于该要素在经济总体中的边际产出水平时，要素资源从其他部门向该部门的转移和流动，就能够提高其自身的整体配置效率，并促进整体经济生产率的提高，而且在应用上来看，与索洛余值法相类似。自进入本世纪以后，对于全要素生产率差额法而言，也逐渐被采用得愈加广泛。如Timmer和Szirmai［7］，以及我国的曾先锋和李国平［8］等人都曾使用过该方法。

3 三种方法各自的适用条件

从转移－份额法来看，尽管其将要素生产率的增长解释为是由产业间的结构效应（要素再配置效应）和产业内的增长效应两方面促成的，但是依据该方法的分析思路可知，产业部门内要素生产率的增长，也应有一部分是由生产要素在产业内各行业间的转移和流动所引起。然而一般来说，在产业结构不断发生变化的过程中，也很可能会同时伴有产业内各行业间的结构性变动。在这种情况下，对于某一产业而言，其部门内要素生产率的增长，本身也会包含产业内各行业间的要素转移和流动所带来的影响。因此，如果将此时经济总体中要素生产率的增长全部解释为产业间要素转移和产业内生产率增长所形成的综合影响，就会产生重复计算产业内生产率增长的嫌疑，并使得估计到的要素再配置效应偏离其实际值。所以，对于转移－份额法而言，应主要适用于测度那些产业结构发生变动、产业内各行业之间的结构没有发生变动或变动很小条件下的要素再配置效应。

对于索洛余值分解法而言，其对要素再配置效应做出准确测度的前提，是将除资本和劳动以外所有影响经济增长的非技术因素全部分解出并加入到新古典模型之内。然而我们知道，在现实中，除了生产要素之外，还存在着很多影响经济增长的其他“非技术因素”。因此在采用该方法时，就要求我们必须能够尽可能地挖掘出影响经济增长的诸多现实因素，并且能够进一步以可获取的数据指标来对这些因素进行反映和衡量。

不难发现，与转移－份额法相类似，对于全要素生产率差额法而言，本质上也是将全要素生产率的增长解释为是由产业间的结构效应和产业内的增长效应两方面促成的。这也就意味着，当要素的转移和流动在产业间以及产业内同时发生时，应用该方法对要素再配置效应进行测度，也会导致估计的结果偏离其实际值。因此关于这一方法，也主要适用于测度那些产业结构发生变动、产业内各行业之间的结构没有发生变动或变动很小条件下的要素再配置效应。

4 结论

要素再配置效应理论虽已不可称之为一个新兴话题，但由于产业结构的变动和调整是世界各国在经济发展过程中所持续经历和发生的，因此围绕要素再配置效应问题所展开的相关讨论，始终是学术界的一个热点领域。也正是因为如此，在近些年来，国内外关于要素再配置效应问题的相关研究，不仅远远没有止步，而且还表现为逐渐地增多。而对于将调整经济结构作为当前经济发展主旋律的中国来说，在未来的一段时期内，通过选择和应用合适的度量方法来对我国产业、行业和地区间的要素再配置效应问题展开讨论，并以此为基础，探讨和挖掘我国要素配置结构的未来改革方向，不论是对于“转方式”“调结构”战略的有效落实，还是对于促发展目标的有效实现，都将有着十分重要的现实指导意义。

［1］Chenery H B，Robinson S，Syrquin M.Industrialization and growth：a comparative study［M］.Oxford：Oxford University Press，1986.

［2］Feder G.Growth in semi－industrial countries：a statistical analysis［M］／／Chenery H B，Robinson S，Syrquin M.Industrialization and economic growth.Oxford：Oxford University Press，1986.

［3］Syrquin M.Productivity growth and factor reallocation［M］／／Chenery H B，Robinson S，Syrquin M.Industrialization and growth.Oxford：Oxford University Press，1986.

［4］Fabricant S.Employment in manufacturing，1899－1939：an analysis of its relation to the volume of production［J］.NBER Working Paper，1942.

［5］Massell B F.A disaggregated view of technical change［J］.The Journal of Political Economy，1961，69（6）：547－557.

［6］Solow R M.Technical change and the aggregate production function［J］.The Review of Economics and Statistics，1957，39（3）：312－320.

［7］Timmer M，Szirmai A.Productivity growth in asian manufacturing：the structural bonus hypothesis examined［J］.Structural Change and Economic Dynamics，2000，11（4）：371－392.

［8］曾先锋，李国平.资源再配置与中国工业增长：1985～2007［J］.数量经济技术经济研究，2011（9）：3－18.