潜艇耐压结构径向初挠度计算方法试验

朱晓军，王 鹏，朱志洁

(海军工程大学船舶与海洋工程系，湖北武汉430033)

0 引言

潜艇耐压结构通常设计成圆柱、圆锥、球面等断面形状规则的几何体，在受到均布载荷作用时，断面不会产生变形;但当受到非均布载荷作用时，断面会出现偏离纯圆的径向初挠度，将会由于弯矩作用产生附加弯曲应力，从而使结构受力状态发生变化。大量结构模型实验表明，结构的毁坏，大多是从出现径向初挠度比较大的部位开始的［1］。由此可见，潜艇耐压结构断面径向初挠度直接影响着其结构强度［2］。因此，在潜艇耐压结构的建造过程中，其径向初挠度的控制是关系潜艇建造质量的重要因素，这就使得径向初挠度的准确评定成为保证潜艇建造质量的关键一环。

现在船厂为了获得耐压结构径向初挠度，主要是通过测量和评定2个步骤，在保证测量环节准确性的基础上，如何更加精确地评定初挠度误差也是一个重要环节，而进行初挠度评定的关键就是利用测量数据确定评定中心。目前国内对潜艇耐压结构径向初挠度测量大都是采用撑尺法［1］，该方法测量过程中需要施工人员找出一个或者多个评定中心，增加了人为误差，降低了测量精度，同时国内至今没有对撑尺法测量潜艇耐压结构径向初挠度的准确度和精确度进行可靠性分析，导致艇体结构强度可靠性分析缺少基本依据。

近年来，国内针对大尺寸圆形构件变形检测的研究越来越多，张福民等对分段制造中大尺寸测量的关键算法进行了研究［3］，周奇才等对地铁隧道变形监测的数字图像处理技术展开了研究［4］，陆峰对地下隧道倾斜洞门中心三维空间拟合进行了研究［5］。现有的研究大多是利用最小二乘圆法对构件变形进行评定，除了最小二乘圆法，GB/T7235-2004提出的评定圆度误差的方法还包括最小区域圆法、最大内接圆法和最小外接圆法，本文旨在通过比较分析应用这4种方法评定潜艇耐压结构径向初挠度时的优缺点，针对不同的工况要求，选择合适的评定方法，更好地指导潜艇耐压结构的制造工艺工程，保证其建造质量。

1 计算原理

潜艇耐压结构径向初挠度评定的范围仅限于建造过程中布置的有限个母线划分点。在实际评定过程中，若母线划分点的初挠度在保证结构强度允许的范围内，则该耐压结构的建造精度是符合要求的，不需要对其进行超差加强，否则要对其进行超差加强从而满足结构强度要求。本文借用GB/T7235-2004提出的4种评定圆度误差的方法中的拟合圆圆心作为潜艇耐压结构母线划分点径向初挠度的评定中心，以该评定中心到各母线划分点的距离与耐压结构设计半径之差作为初挠度值。以下主要对4种圆度误差评定方法中如何获得拟合圆心进行阐述。

1)最小二乘圆

最小二乘圆 (least squares mean circle，LSC)是使实际被测轮廓上所有测量点到其圆心的径向距离平方和最小的圆。根据最小二乘圆的定义，设参考圆的圆心为 (a0，b0)，任意一个母线划分点的坐标为 (xi，yi)，要获得参考圆圆心，必须使得所有测量点到其圆心距离的平方和取到最小值［6］，即:

取到最小值，从而得到圆心坐标为

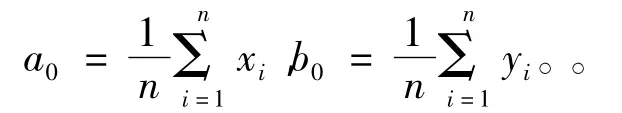
2)最小区域圆

寻找两同心圆与被测轮廓至少有4个公共点，且轮廓上其他点都落在两同心圆所组成的圆环之间，则同心包容圆中半径差最小的一对同心圆即为最小区域圆 (minimum zone circle，MZC)。根据最小区域圆的定义，需要通过多次移心才能找到满足条件的圆心，每次移心都要确定移心方向和移心步长，移心方向要以满足使2个同心包容圆的半径差减小的充要条件为基础，保证原有接触点仍在新的内接圆上，还要针对具体接触情况，选择半径差减小速度最快的方向。通过不断移动圆心，使2个同心包容圆的半径差不断减小，直至找到与实际轮廓曲线有4个内外相间的交错接触点为止。

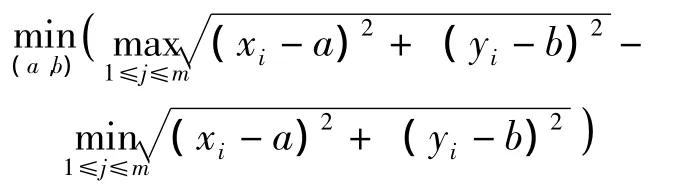
来确定［7］。

3)最小外接圆与最大内接圆

包容实际被测轮廓的半径最小的圆即为最小外接圆 (minimum circumscribed circle，MCC)，被实际轮廓包容的半径最大的圆即为最大内接圆(maximum inscribed circle，MIC)。最小外接圆和最大内接圆按照直线准则或三角形准则［8］来确定。直线准则，当最小外接圆包容实际被测轮廓或者实际被测轮廓包容最大内接圆时，实际轮廓上有2个测点与该圆接触，而由这两点连成的直线恰为该圆的直径;三角形准则，实际被测轮廓上有3个测点与该圆接触，并且这3点连成一个锐角三角形，该圆圆心位于此三角形内部。

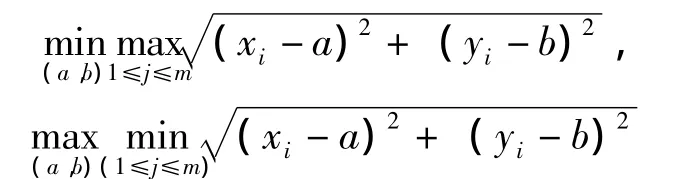
来确定［9］。

2 初挠度评定

2.1 评定中心的确定

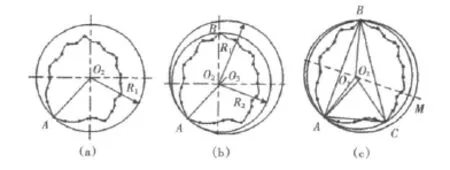
图1 寻找最小外接圆流程图Fig.1 The flow chart for searching MCC

本文所研究的潜艇耐压结构径向初挠度评定问题的重点是评定中心的确定问题，本节所要解决的问题是利用实验测得的数据进行初步处理后进行拟合，得到满足条件的4种拟合圆，并将其圆心作为评定耐压结构径向初挠度的评定中心。最小二乘圆的拟合圆心可以由测量数据的算术平均数确定，最小外接圆与最大内接圆拟合圆心最终都是根据直线准则或者三角形准则进行确定，在最小外接圆的基础上改变圆心，增大半径，使得内外包容圆包容实测轮廓的同时，与其接触点分布为相互交叉的4点，这样就可以确定最小区域圆。本文主要以介绍如何确定最小外接圆法的拟合圆心为例，寻找最小外接圆的基本思路是在找到一个包容轮廓曲线的圆的基础上，按一定的条件逐步缩小这个圆，最后找到最小外接圆。主要经过以下步骤:

1)以最小二乘圆圆心O1为圆心，轮廓曲线上距圆心O1在最远的距离为半径作圆，如图1(a)所示，则该圆半径R1=O1A。

2)缩小圆O1至圆O2，使得找到的圆心O2落在线段O1A上，且该圆与实际轮廓存在2个公共点(点A，B)，其余各点都落在该圆内，如图1(b)所示，则该圆半径R2=O2A。

3)进一步缩小圆O2，得到圆O3，使得找到的圆心O3落在线段AB的垂直平分线O2M上。该圆与实际轮廓曲线存在3个公共点 (点A，B，C)，其余各点都落在该圆内，如图1(c)所示，则该圆半径R3=O3A，且O3A＜O2A;同时可以发现圆心O3在△ABC包容的区域内，或者在点A，B，C任意2点的连线上。

4)重复步骤2和3，并且利用直线准则或者三角形准则，直到找到符合条件的最小外接圆，从而确定拟合圆的圆心。

2.2 初挠度计算

实际工况下，评定潜艇耐压结构径向初挠度只是对其母线划分点的初挠度进行评定，本文利用GB/T7235-2004提出的4种评定圆度误差的方法处理实验数据分别得到拟合的最小二乘圆、最小区域圆、最小外接圆和最大内接圆的圆心，并分别以这4个拟合圆圆心作为潜艇耐压结构母线划分点径向初挠度的评定中心，则母线划分点的径向初挠度:

3 实例验证

3.1 实验数据的记录

使用科利达585R全站仪对Φ3 000mm的圆柱模型径向初挠度进行测量，使用全站仪对被测模型的均匀分布的32个母线划分点进行测量，并对原始数据进行初步处理，得到测量点在评定平面上的投影点的二维坐标，如表1所示。

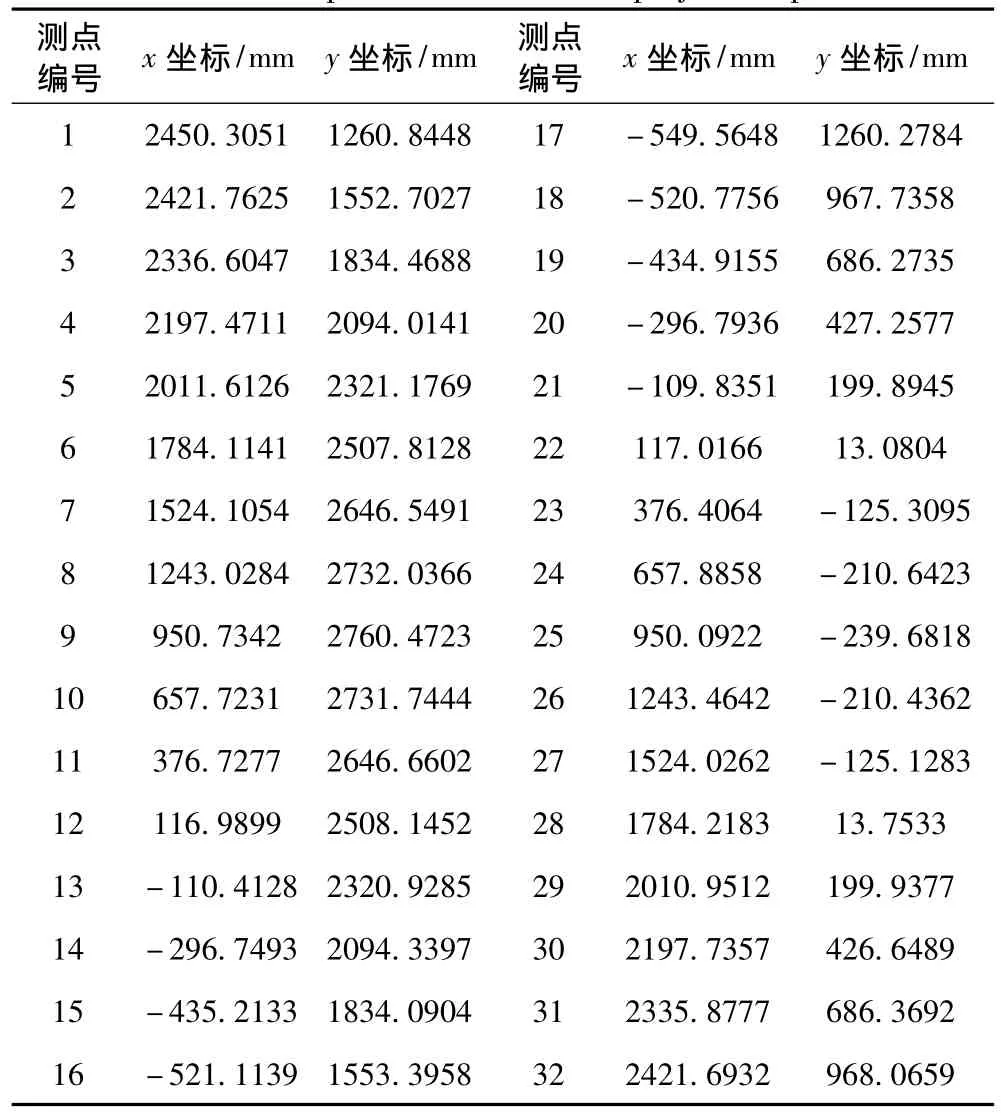
表1 投影点二维坐标Tab.1 The planar coordinate of projection points

3.2 数据计算结果分析

当耐压结构母线划分点径向初挠度的评定结果小于0.002 5R0时，则认为该点出现的径向初挠度在结构强度允许的范围内。将实验测量数据导入到编写的程序中进行计算，得到根据不同的评定中心计算的初挠度评定结果，4种方法的评定中心以及评定合格率如表2所示。

表2 初挠度评定合格率比较Tab.2 The eligible proportion of radial initial deflection evaluating

以最小二乘圆法得到的评定初挠度结果为参考值，其他3种方法评定结果与参考值相比较，可以发现:最小二乘圆法评定的初挠度值最大，最小区域圆法评定的初挠度值最小，如图2所示。初挠度评定不合格的母线划分点需要进行超差加强，若采用最小二乘圆法评定的结果为参照对耐压结构进行超差加强，则需要耗费的人力物力资源较多，并且在进行超差加强时的精度不高，但总的来说可以保证更高的潜艇结构的安全性;若采用最小区域圆法评定的结果为参照对耐压结构进行超差加强，则需要耗费的人力物力资源相对较少，进行超差加强时的精度相对提高，但是只能保证满足潜艇结构安全性的基本要求。

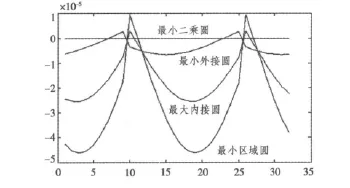
图2 四种方法评定结果比较Fig.2 The result comparative chart of four methods

4 结语

本文对潜艇耐压结构径向初挠度的计算问题进行了阐述，并利用评定圆度误差的最小二乘圆法、最小区域圆法、最大内接圆法、最小外接圆法的拟合圆心作为初挠度的评定中心。试验验证表明:最小区域圆法评定精度最高，得到的耐压结构母线划分点的初挠度评定合格率最高，需要对较少的母线划分点进行超差加强，但其算法复杂，运算时间较长，主要用于精度要求较高的场合;最小外接圆法和最大内接圆法的评定精度次之，但其算法简便、运算时间短;最小二乘法评定精度最低，得到的耐压结构母线划分点的初挠度评定合格率最低，需要进行超差加强的点比较多，但对于潜艇耐压结构强度要求来说是一种安全性比较高的算法，可用于精度要求不高的场合。考虑到保证潜艇耐压结构强度的同时，尽量减少工作量以及建造成本今后还要对评定方法的选择与结构安全性之间的权重关系作进一步研究。

［1］邱桂林.潜艇建造工艺学［M］.北京:国防工业出版社，1982.236-255.

［2］王永军，万正权，祁恩荣，等.考虑大挠度影响的球形壳强度与变形分析［J］，舰船科学技术，2010，32(1):42-47.WANG Yong-jun，WAN Zheng-quan，QI En-rong，et al，Strength and deformation analysis of dome shell considering the large deflection effect［J］.Ship Science and Technology，2010，32(1):42-47.

［3］张福民，曲兴华，叶声华.分段制造中大尺寸测量的关键算法研究［J］.光电子·激光，2008，19(10):1368-1371.ZHANG Fu-min，QU Xing-hua，YE Sheng-hua.Research on key algorithms for large scale measurement in subsection manufacture［J］.Journal of Optoelectronics Laser，2008，19(10):1368-1371.

［4］周奇才，孙月腾，陈海燕，等.地铁隧道变形监测的数字图像处理技术研究［J］.中国工程机械学报，2009，7(4):463-468.ZHOU Qi-cai，SUN Yue-teng，CHEN Hai-yan，et al.Digital image processing technologies for deformation monitoring on subway tunnels［J］.Chinese Journal ofConstruction Machinery，2009，7(4):463-468.

［5］陆峰.地下隧道倾斜洞门中心三维空间拟合研究［J］.科技创新导报，2009，22:62-63.LU Feng.Study on three-dimensional interspace planning of subway tunnels leaned hole［J］.Science and Technology Innovation Herald，2009，22:62-63.

［6］石章松，逯建军，郑鹏，等.一种三维空间目标被动跟踪算法［J］.海军工程大学学报，2011，23(3):30-34.SHI Zhang-song，LU Jian-jun，ZHENG Peng，et al.An algorithm for target passive tracking in three dimensional space［J］.Journal of Naval University of Engineering，2011，23(3):30-34.

［7］彭晓南，刘飞，雷贤卿.基于最大内接圆法的圆度误差测量实现方法［J］.工具技术，2008，42(1):118-121.PENG Xiao-nan，LIU Fei，LEIXian-qin.Evaluating algorithm of roundness error based on maximum inscribed Circle［J］.Tool Engineering，2008，42(1):118-121.

［8］刘顺芳，倪素环.最小外接圆法评定圆度误差值的计算机实现方法［J］.计量技术，2006，2:26-29.LIU Shun-fang，NI Su-huan.Minimum circumscribeb circle method for evaluation of the errors of the circle roundness by using programmer method［J］.Measurement Technigeu，2006(2):26-29.

［9］潘国荣，张鹏，孔宁.造船精度控制系统中用移站测量获取点位信息的一种方法［J］.大地测量与地球动力学，2010，30(5):121-124.PAN Guo-rong，ZHANG Peng，KONG Ning.A stationmoving measurement method for acquiring point position information in precision control system for ship building［J］.Journal of Geodesy and Geodynamics，2010，30(5):121-124.