基于差分自回归移动平均模型的城市火灾趋势预测

●张晓珺

(杭州市消防支队，浙江杭州 310016)

随着我国经济发展、城市化进程加快，城市火灾的危害程度日益加剧。近年来，城市火灾的发生呈现明显的上升趋势。城市火灾的多发，不仅造成了严重的财产损失和人员伤亡，而且也影响了城市的经济建设和社会政治稳定。因此，对城市火灾的发展变化规律进行研究显得尤为重要。而城市火灾是随时间而变化的事件，它是一个时间序列，有其自身的特点和规律。本文以火灾风险统计数据中的火灾发生起数为研究对象，通过研究城市火灾时间序列中数值上的统计相关关系，揭示城市火灾的发展变化规律。

目前，时间序列预测方法有经典的统计方法、神经网络和机器学习等［1］。一般情况下，预测的基本数据是时间序列数据，也就是按照时间顺序先后存放在数据库中的数据，已经有不少使用时间序列模式进行预测的研究成果［2－3］。时间序列建模的目的之一就是对动态数据进行预测或预报，以便对系统的特性进行处理或控制［4］。1968年Box和Jenkins提出了一套比较完整的时间序列建模理论和分析方法，即著名的“Box－Jenkins法”，它通过经典的数学方法建立随机模型，如自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型和差分自回归移动平均(ARIMA)模型等，进行时间序列的预测。

1 ARIMA模型的定义与基本思想

Box－Jenkins法的模型符号一般写作 ARIMA(p，d，q)(P，D，Q)S。其中，AR代表自回归模型，MA代表移动平均模型，I表示两种方法的结合，p代表自回归阶数，q代表移动平均阶数，d代表对含有长期趋势、季节变动和循环变动的非平稳序列进行差分处理的次数，使其平稳且符合自回归模型的需要，P、D和Q分别表示季节自回归阶数、季节差分次数和季节滑动平均阶数。这样，可以把该模型的通式写成以下的形式［1］:

模型由两部分组成，前半部分是p阶的自回归方程;后半部分是q阶的误差移动平均(多项和形式)方程。模型体现了对p阶自回归模型的误差进行q阶修正的预测思想。由于模型以多项和形式出现，因此，p、q可以根据实际情况进行伸缩，使模型能适应于多种类型的时间序列。

ARIMA模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。

2 城市火灾的ARIMA模型预测步骤

2.1 数据的预处理

平稳时间序列可以看作是一种线性转换装置，它将白噪声信号转换为所描述的时间序列。根据时间序列的散点图、自相关函数和偏自相关函数图以ADF单位根检验其方差、趋势及其季节性变化规律，对序列的平稳性进行识别。如果一个序列的平均值和方差始终为常数，则称它为平稳的。如果数据图呈现线性或非线性趋势，则时间序列是不平稳的。如果自相关函数在前面少数几个值后下降为0，则序列是平稳的;如果在前几个值后没有下降为0，而是逐次减少，则序列不平稳。

2.2 模型的识别、定阶与参数估计

对乘积季节模型的阶数识别及参数估计，基本上立足于考察数据的样本自相关、偏自相关函数［5］。如果样本自相关、偏自相关函数既不截尾也不拖尾，而且不是呈线性衰减趋势，相反的，在相应于周期S的整倍数点上，自相关(或偏自相关)函数出现绝对值相当大的峰值并呈现振荡变化，就可以判断数据序列适合于乘积季节模型。

关于差分和季节差分阶数d、D的选取，可采用试探法，也可利用信息准则。差分阶数d、D宜取较低阶(通常取1、2或3)。若对于某一组d、D得到的自相关(或偏自相关)函数呈现较好的截尾或拖尾特性，则认为相应的d，D是适宜的。利用信息准则，即定义一个与模型阶数信息有关的特征参数，从而选取使它达到最小值的阶数作为模型的阶数，其中，Akaike的信息准则(AIC)是适应性非常广泛的准则，可用于确定模型的最佳阶数。定义AIC准则函数为［1］:

可见，AIC准则函数由两项构成，第一项体现模型拟合的好坏，它随着阶数的增大而变小;第二项标志了模型参数的多少，即模型的复杂程度，随着模型参数的增加而变大。AIC同时体现了残差不相关原则和模型简洁原则的结合，并且排除了建模者的主观因素。

作为对这一方法的改进，Akaike和E.J.Haman等人提出了 BIC 准则［1］:

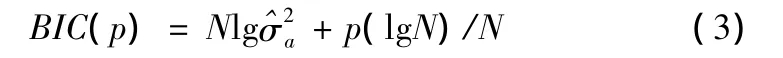
同样，使得BIC最小的p值就是最佳阶数。当阶数d、D确定后，模型参数p、q、P、Q的估计一般采用最大似然估计和无约束最小二乘。

2.3 模型的诊断检验

ARIMA乘积季节模型的诊断检验，即模型的残差序列的独立性检验，若残差序列不是白噪声序列，说明残差序列中还存在有用的信息未被提取，需对原模型进一步改进，从而得到更适合的模型。

2.4 利用已通过检验的模型进行预测分析

经过以上的建模和检验、判别后，就可以使用人们能够认可的ARIMA模型进行逐期递推预测，并给出置信区间。

3 基于ARIMA模型的城市火灾趋势预测

本文以北京市2000～2006年月火灾统计数据为例(如图1所示)，建立ARIMA乘积季节模型并对2007年月火灾发生起数进行预测。

3.1 序列的平稳性处理

对北京市2000～2006年火灾起数时间序列观察其自相关和偏自相关图，并对其进行平稳性(ADF)检验，发现原时间序列不平稳。为了消除原始数据序列的不平稳性，本文采用对月火灾起数取对数形式。由于原序列存在趋势性和季节性，对原始序列在对数基础上进行一阶差分和一阶季节差分，差分后的序列图如图2所示，可见趋势性和季节性基本消除，可认为是平稳序列，但序列图只能粗略的判断序列具有平稳性，理论上应进行检验。应用单位根检验方法，得到ADF Test Statistics结果为 － 7.234647，1% 临界值为 － 3.7304，5% 临界值为 －2.985，10% 临界值为 －2.6328，可知其平稳性，ARIMA模型中d和D应取1。

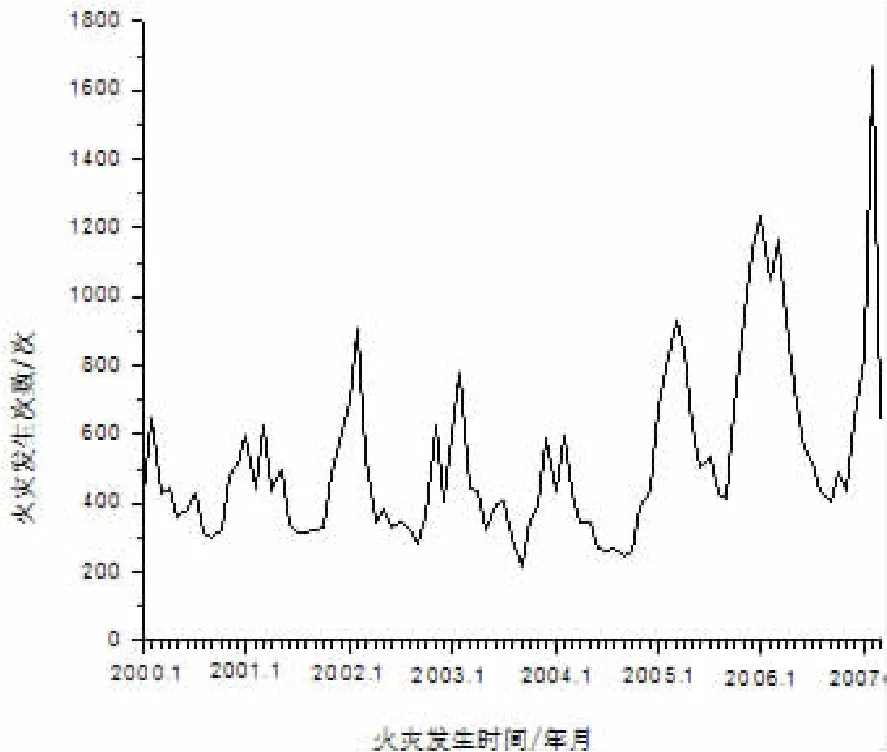
图1 北京市火灾发生起数时间序列

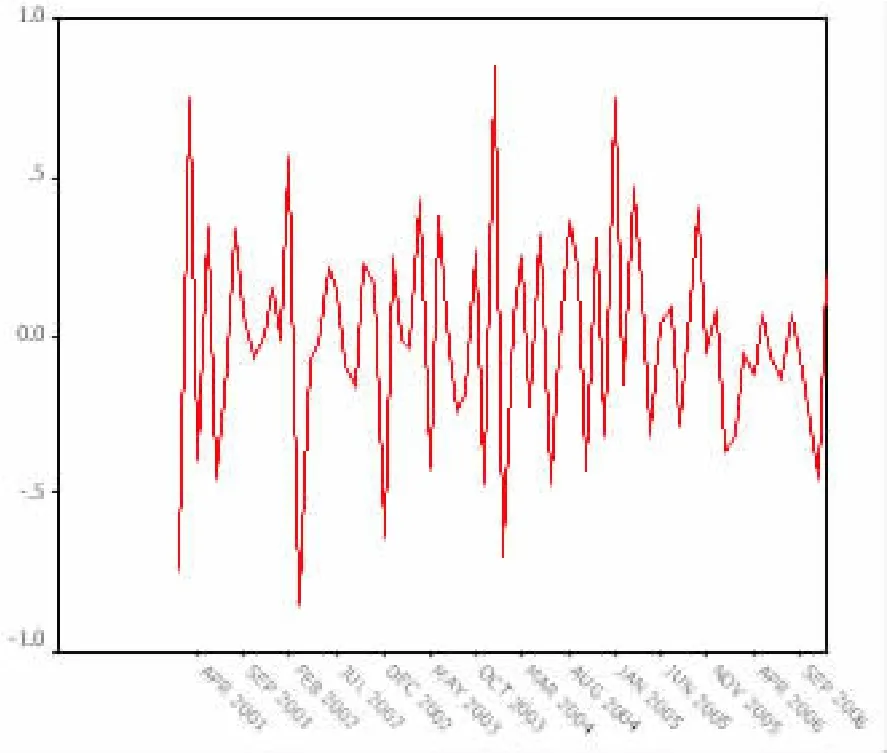
图2 差分后的时间序列图

3.2 模型的识别与建立

经差分平稳后，确定p、q和P、Q:当不包含时滞k=12(或4)、24(或8)等时，p取落入随机区间之外的偏自相关系数PAC的个数或与0有显著差异的PAC的个数，q取落入随机区间之外的自相关系数ACF的个数或与0有显著差异的ACF的个数。当仅观察时滞k=12(或4)、24(或8)等时，P取显著不为0的偏自相关数目，Q取显著不为0的季节自相关数目。由图3和图4可以判断出，p、q分别取1，P和Q分别取0和1，此时信息量准则统计量AIC为804.189，BIC为813.16063，本文所选取的乘积季节模型为 ARIMA(1，1，1)(0，1，1)12。

3.3 模型诊断检验

白噪声残差检验见表1，P＞0.05，x2检验表明不能拒绝残差不相关的零假设，即所建立的模型是合适的。

3.4 模型的预测

利用 ARIMA(1，1，1)(0，1，1)12模型对2007 年1 至12 月的月火灾起数进行预测，结果见表2。

图3 差分后的自相关图

图4 差分后的偏自相关图

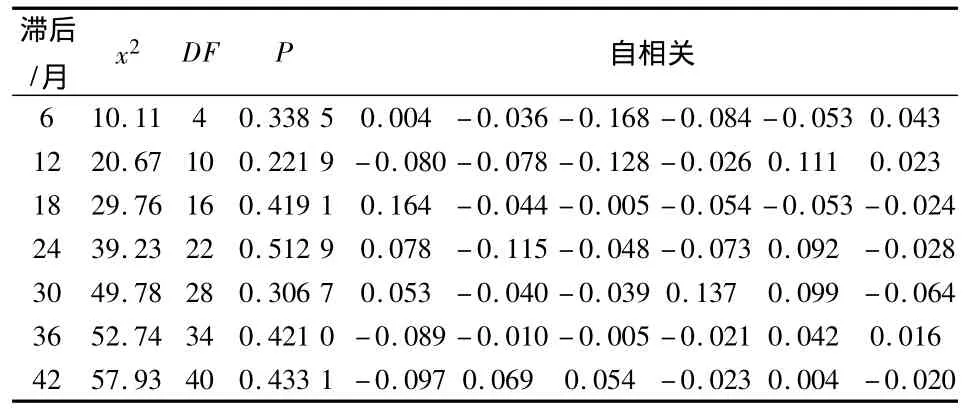
表1 残差序列的自相关检验

4 结论

本文以火灾统计数据中的火灾发生起数为研究对象，利用时间序列分析中的季节乘积模型ARIMA对城市火灾进行预测。以北京市2000～2006年火灾数据为例，建立了预测模型 ARIMA(1，1，1)(0，1，1)12，进而预测了北京市 2007 年月火灾发生起数，并与实际值相比较，发现其绝对误差与相对误差都在合理范围区间，说明该模型预测结果较好，可用于对火灾作短期预测，预测结果可为消防部门的决策提供科学依据。

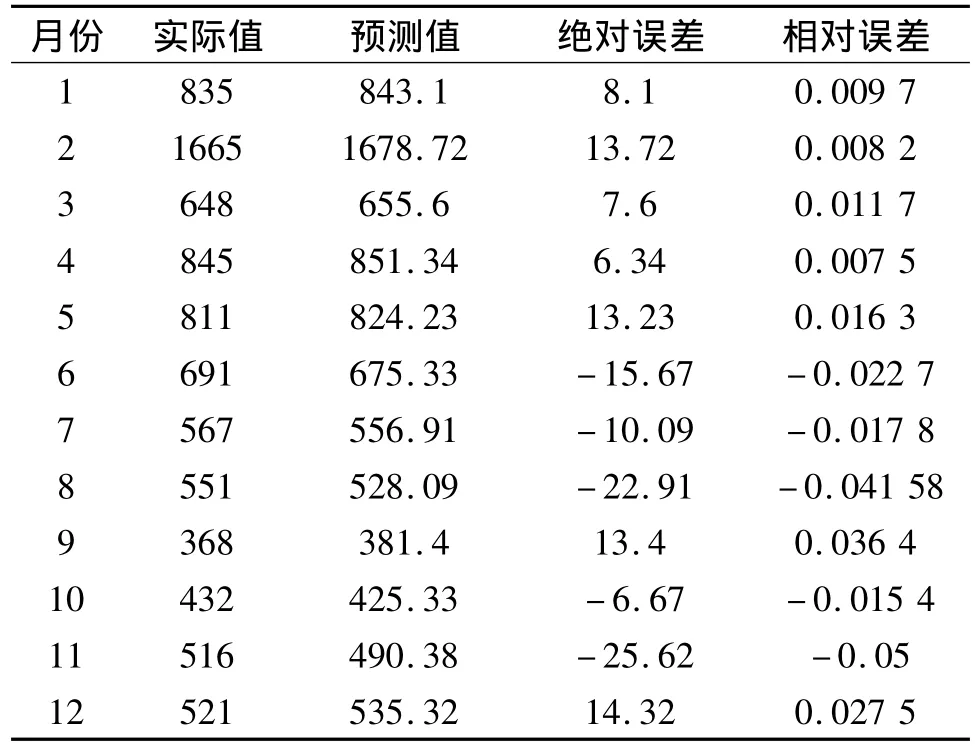
表2 月火灾起数预测结果

［1］陈安，陈宁，周龙骧.数据挖掘技术及应用［M］.北京:科学出版社，2006:253－256.

［2］Rakesh Agrawal，Ramakrishnan Srikant.Mining sequential patterns［C］//Proceedings of 11th Conference of Data Engineering，1995:3 －14.

［3］Ramakrishnan Srikant，Rakesh Agrawa.Mining sequential patterns:Generalization and performance improvement［C］//Proceedings of 5th Int.Conf.Extending Database Technology，1996，1057:3 －17.

［4］吴今培，孙德山.现代数据分析［M］.北京:机械工业出版社，2006:224－230.

［5］涂雄苓，黄月玲.旅游需求预测的ARIMA乘积季节模型构建及实证分析——以桂林市为例［J］.广西财经学院学报，2011，(1).