一种基于分层分析算法的实时最优消防应急救援路径算法

●李超鹏

(太原市消防支队，山西太原 030024)

随着我国社会经济的快速发展，城市规模迅速扩大，各类型火灾发生频率逐渐增大，这直接威胁人民群众的生命财产安全。消防救援作为社会的保障力量，能否及时到达火灾发生地点实施救援至关重要，因而救援路径的选择是关键。目前典型的消防救援路径选择算法是Dijkastra算法及其改进算法［1－4］，这些算法适用于距离是衡量路线优劣惟一标准的情况，这就要求路网畅通度好，道路规格较高及较少的交叉路口等［5］。但是在实际的救援工作中，路网中不同路段的畅通度，道路规格及交叉口数量差别很大，而且路网是动态变化的，经常会发生由于无法预测的因素延误应急救援力量到达被救援地点的时间，影响救援效果，造成不必要的人员伤亡或经济损失。本文提出了一种实时的分层分析算法计算最优路径。该方法不仅考虑了路网中不同路段的畅通度、道路规格及交叉路口数量等因素，同时还充分考虑路网状态实时变化，使用局部规划技术应对突发事件，修正全局路径，保证车辆行驶时间最短。实验结果表明，该算法可以作为应急救援路径选择的依据，同时实际应用证明该算法有效可靠。

1 基于分层分析算法的消防救援路径规划

现有典型的最短路径算法是Dijkastra算法及其改进算法，算法的基本思想是遍历起点到终点的道路进而选择最短的路径。然而实际情况并非如此，如应急救援车的车重是否超过桥梁限重，应急救援车的车高是否可以穿过高架桥，应急车辆经过的道路交叉口延误是否交叉及应急车辆通行路段是否进行交通管制等等。所以不能只考虑道路长短。使用层次分析法可以将上述情况纳入考虑，得出最优应急救援路径。

1.1 层次分析法

人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。用层次分析法建模，可分为三个步骤首先建立递阶层次结构模型，其次构造出各层次中的所有判断矩阵，最后进行一致性检验。

1.2 消防应急求援道路层次结构模型

本文将消防求援车辆到达救援地点时间最短作为决策目标，综合考虑了道路规格、道路通行方向，道路行驶时间，交叉路口延误时间作为影响决策因素，得出如下结构模型见图1。

1.3 构造判断矩阵

根据图1层次结构模型以及多位专家对指标的评价意见，可得出影响道路权值因素的重要性排序，B1＞B2＞B3=B4，并构造出各层次的判断矩阵，然后采用和法计算得到权重。对于目标O构造的各影响力因素Bi的相对重要性判断矩阵O－B见表1。同理构造出判断矩阵B－C的权重，排序见表2。

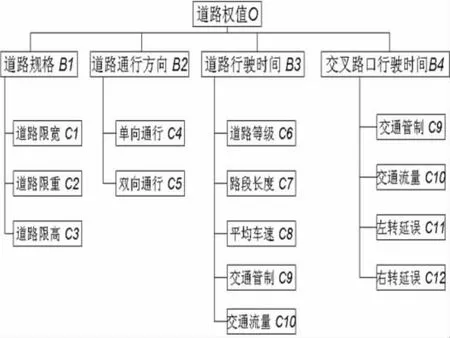
图1 消防应急求援道路层次结构模型

表1 相对重要性判断矩阵O－B

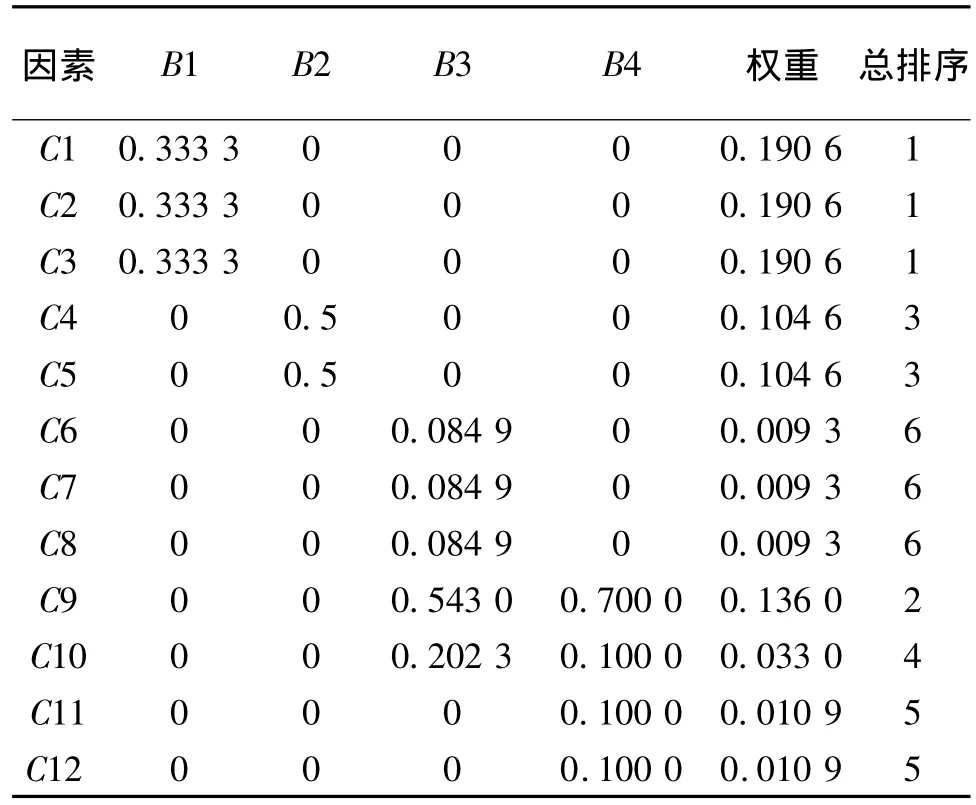
表2 相对重要性判断矩阵B－C及特征向量

以上计算结果一致性检验通过。上述结果表明，在所有影响应急救援行动到达被救援地点时间的因素中，道路限宽、限高、限重是需要首先考虑的因素，其次交通管制、道路通行方向以及交通流量等因素对救援车辆到达时间影响权重较大。这与实际情况相符，也从另一个角度验证了计算结果。

1.4 无纲量化属性数据

由于道路属性是从不同的角度来描述道路形态，因而各个道路属性的单位不同，例如路段车速单位是km·h－1，路段长度单位是km，而左/右转延误单位是min，为便于将不同属性数据统一进行计算就是属性数据的无纲量化。本文使用成本型属性集的无纲量化标准函数进行无纲量化，对于任一属性pi∈U，其取值范围为［mi，Mi］，则无纲量化后属性 ri为:

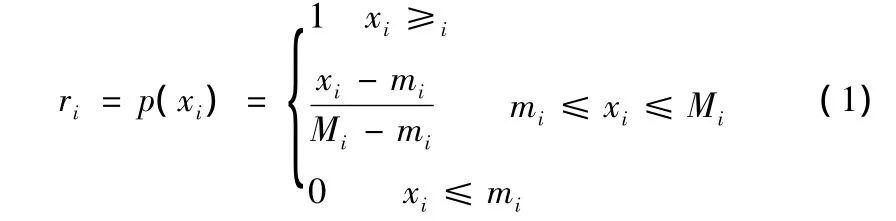
如果道路属性 C1，C2，…，C12 对应的权值为 ω1，ω2，…，ω12，无纲量化后的对应属性为 r1，r2，…，r12，消防应急求援时间T为:

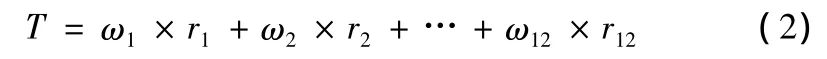
1.5 基于分层分析法的最优路径

从前文利用层次分析法求得的路段权值分别赋予各个路段，因而分层分析法求得最优路径数学模型为，将路网定义为一个赋权图G(V，E)，每一边e(vi，vj)对应权值表示为w(e)，设R是起点Vs到终点Vt所有路径的集合，r为其中一条路径，r∈R，路径r的权为w(r)即w(r)=∑w(e)，目标是求得一条起点Vs到终点Vt权最小的路径r0，即w(r0)=minw(ri)。基于分层分析法的最优路径算法基本流程如下:(1)车辆由起始点S向目标节点T行驶，定义集合S={Vs}，T={其余顶点}，w(Vs，Vi)＜ Vs，Vi＞ 弧上的权值。T中顶点对应的权值w(Vs，Vi);(2)从T中选取一个其权值为最小的顶点Ti，且该顶点不在S中，将Ti加入S;(3)对其余T中顶点的权值进行修改，若加进W作中间顶点，从V0到Vi的权值变小，则修改此权值。重复步骤(2)、(3)，直到S中包含所有顶点为止。

2 基于分层分析算法的实时最优消防应急救援路径路径规划

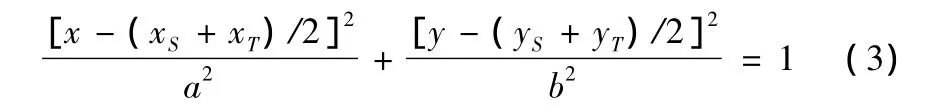
其中，x、y为椭圆任意点的坐标，xS、yS、xT、yT分别为起点S、终点T的坐标。a、b分别为椭圆长短轴。本文章椭圆的a、b值选取过程如下:(1)首先从太原市一中队辖区电子地图855个点中随机选取30个点，放入集合A和B中，并计算其笛卡尔乘积C=A×B={(a，b)|(a∈A)∧(b∈B)};(2)集合C中含有900对点，求取集合C中900对点的直线距离与最短路径比值放入集合R;(3)对集合R进行统计分析得出特定系数，该系数需满足95%置信水平，且其值不大于5。本算法选取集合R中元素的算术平均值满足该条件。经计算，集合R中元素的算术平均值该值为1.543;(4)按如下公式计算椭圆长袖2a，短轴 2b。

层次分析法是在给定路网结构和交通流分布信息的情况下，综合考虑道路规格、交通管制及交通流量等因素，将路网抽象为不同层，提供从起点到目的地的全局最优/最短行驶路径。但是路网状态时实时动态变化的［6］，例如突发的交通事故。该算法不能充分考虑路网状态实时变化，难以应对路网中的突发事件，因而在车辆出行的最短路径中需要使用局部规划技术应对突发事件，修正全局路径，保证救援车辆到达目的地行驶时间最短。

现有的局部规划技术是通过限定搜索区域实现的，典型的限定搜索区域方法包括圆形法［7］、椭圆法［8］、椭圆外切矩阵［9］、椭圆内含矩阵［10］等。由于椭圆法被证明具有较高的可信度，同时椭圆区域大小依赖于统计经验，由于每个消防基层中队辖区内道路数量有限，因而具有很强的可行性。综上两点本文选用椭圆作为限定搜索区域。假设出行的起点为S到目标点为T，椭圆方程为:

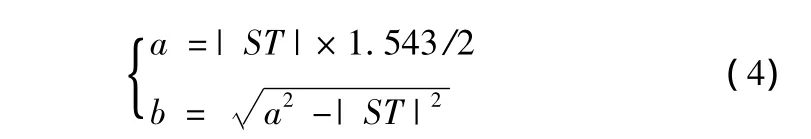
椭圆限制算法给出的置信水平95%，表明在椭圆内找不到全局最短路径的可能行不大于5%，即使是剩下的5%不是全局最短路径也至少是局部最短路径，所以一般认为这5%是完全可以忽略的。在获得了限制搜索区域的基础上。具体的算法流程如下。

2.1 算法基本流程

步骤1:车辆沿着层次分析法得出的全局规划路径R，由起始点S向目标节点T行驶，直到如下中某种情况出现:(1)到达目标节点Ti停止搜索;(2)车辆到达节点i时，路段(i，j)出现障碍物(如突发事件、交通堵塞，该数据来源于交通指挥系统)，转自步骤2。

步骤2:重置该路段(i，j)权值Wi

步骤3:在椭圆区域内(节点i作为新的起点S，目标节点T不变)重新计算替代路径。重新计算好的替代路径与椭圆区域外的全局规划路径形成新的全局路径。

步骤4:沿着新得到的路径前进，直到如下中某种情形出现:(1)到达目标节点Ti停止搜索;(2)车辆到达节点i时，路段(i，j)出现障碍物(如突发事件、交通堵塞)，转自步骤2。

2.2 实验验证及结果分析

实验过程中本文首先使用MapInfo建立太原市一中队辖区的消防救援电子地图，该电子地图主要图层有:重要道路图层，一般道路图层，小路图层，消防中队图层，消防安全重点单位图层，一般单位图层，水源分布图层及消火栓分布图层。

实验假设太原市一中队辖区内某大厦发生火灾，以太原市一中队为起点，该大厦为终点选取最优路径。该大厦位于师范街中段，党校路东侧，坞城中路西侧，该大厦南侧紧邻居民区，且楼间距较近。该大厦共32层，1－3层是商场，4－10层为写字楼层，10层之上为居民住宅。由于人口密度大，不易疏散，极易造成人员伤亡，需调派高空消防云梯车、抢险救援消防车和水罐消防车前往救援。消防车参数见表3。

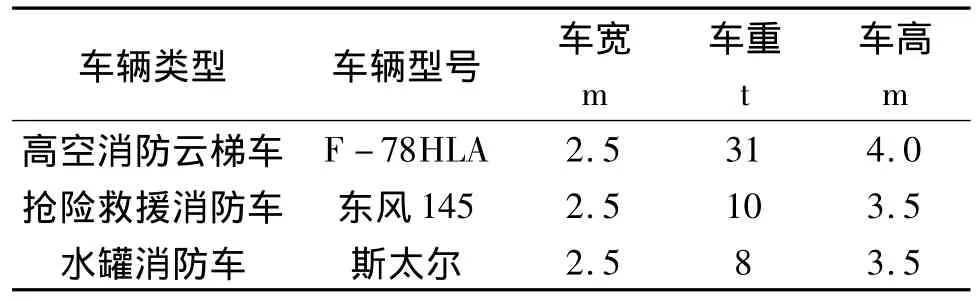
表3 消防车参数表

消防一中队位于起火点西北部，有多条路径可通往救援。图2为未出现局部堵塞时最优路径方案，其中虚线路径为分层分析算法与实时分层分析算法计算得到的结果，实线路径为Dijkastra算法计算得到的结果。表4是图2对应的计算结果。图3为党校路出现堵塞时最优路径方案，其中虚线路径(小间隔)为分层分析算法计算得到的结果，虚线路径(大间隔)为实时分层分析算法计算得到的结果，实线路径为Dijkastra算法计算得到的结果。椭圆是以军民路与党校路十字路口为新的起点和起火点为终点形成的椭圆搜索区。表5对应图3计算结果。

图2 未出现局部堵塞时最优路径方案

表4 在未出现局部堵塞时最优路径方案比较表

图3 出现局部堵塞时最优路径方案

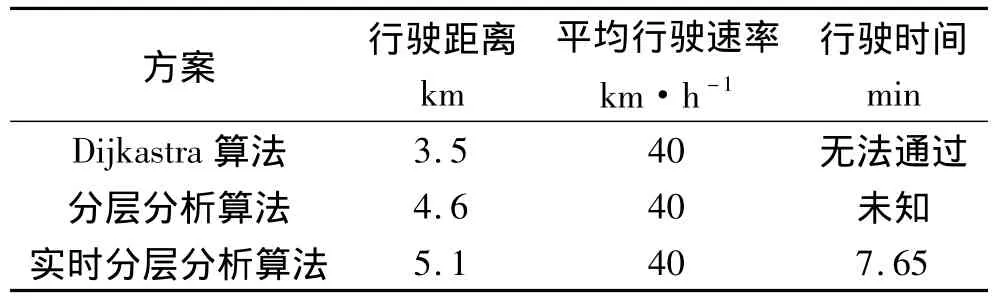
表5 出现局部堵塞时最优路径方案比较表

从视觉测量(图2、3)及数理统计(表4、5)两方面进行分析比较可知:(1)在未出现局部堵塞时，分层分析算法与实时分层分析算法得到最优路径方案相同，且都比Dijkastra算法得到的最优路径方案距离较长。但是Dijkastra算法得到的最优路径方案经过八一路是县道，且路口较多，因而交叉路口延误时间较长，会增加车辆行驶时间。同时，八一路较窄，仅能通过抢险救援消防车，而高空消防云梯车、水罐消防车无法顺利通过，因而Dijkastra算法得到的最优路径方案不可行。而分层分析算法与实时分层算法得到最优路径方案经过平阳路与学府街是两条省道，路口较少，可通过交通流量更大，同时路面宽敞，抢险救援消防车，高空消防云梯车及水罐消防车都可以顺利通过，是该情况下的最优路段选择。(2)在出现局部堵塞时，以党校路堵塞为例，Dijkastra算法得到路径方案与未出现局部堵塞时相同，因而不具有可行性。实时分层分析算法得到的路径方案在距离上较分层分析算法得到的路径方案较长，但是分层分析算法路径方案在堵塞路段等待通行时间未知，而实时分层分析算法得到的路径方案是较分层分析算法得到的路径方案的局部次优方案，且到达起火点时间明确，因而实时分层分析算法得到的路径方案是该情况下的最优路段选择。(3)将以上两种情况生成的最优路径与实际情况进行比对，基本符合实际。

3 结论

本文在基于对分层分析算法最优路径的原理和特点的基础上进行研究和分析，提出了一种实时的分层分析算法计算最优路径。该方法充分考虑路网状态实时变化，使用局部规划技术应对突发事件，修正全局路径，保证车辆行驶时间最短。实验结果及实际经验均表明，与典型的Dijkastra算法及分层分析算法比较，该方法得到的最优路径方案均具有更强的可行性。

［1］AHUJA R K，MEHLHORN K，ORLIN J B，TARJAN R E.Faster algorithms for the shortest path problem［J］.Journal of the Association f or Computing Machinery，1990，37(2):213 －223.

［2］严寒冰，刘迎春.基于GIS的城市道路网最短路径算法研讨［J］.中国计算机学报，2002，(2):210 －215.

［3］魏新宇.消防灭火救援最优路径算法研究［D］.西安:西安科技大学，2006.

［4］唐文武，施晓东，朱大奎.GIS中使用改进的Dijkstra算法实现最短路径的计算［J］.中国图象图形学报，2000，5(12):1019－1023.

［5］龙科军，LEE D.HAN，王赛政.路网信息不完备条件下的动态最短路搜索［J］.计算机应用，2011，3(3):651 －653.

［6］王晓丽，杨兆升，吕旭涛，等.平行四边形限制最短路径算法及其在道路网络中的应用［J］.吉林大学学报，2006，36(1):123～127.

［7］YAO Xin，LIU Yong，LIN Guang－ming.Evolutionary programming made faster［J］.IEEE Transactions on Evolutionary Computation，1999，3(2):82 －102.

［8］ZHONG Wei－cai，LIU Jing，XUE Ming－ zhi.A multi－ Agent genetic algorithm for global numerical optimization［J］.IEEE Transactions on Systems，Man，and Cybernetics Part B:Cybernetics，2004，34(2):1128－1141.

［9］LEUNG Y W，WANG Y P.An orthogonal genetic algorithm with quantization for global numerical optimization［J］.IEEE Transactions on Evolutionary Computation，2001，5(1):41 －53.

［10］SHANG Yun －wen，QIU Yu－huang.A note on the extended rosenbrock function［J］.IEEE Transactions on Evolutionary Computation，2006，14(1):119 －126.