基于高阶统计量的短波通信信号特征分析＊

薄 远 朱卫纲 盛 莹

（1.装备学院 北京 101416）（2.63888部队 济源 454650）

1 引言

人们对信号进行处理，其最终目的就是要对单通道或多通道的有限长观测数据进行必要的处理，从而检测出隐含于这些观测数据中的各种重要信息并加以利用。高阶统计量在信号处理与系统分析中扮演着一个极为重要的角色。根据最近的资料显示，在通信、生物医学工程、语音处理、地震信号分析、图象处理、雷达、声纳等领域都进行了有关高阶统计量处理的研究，具体应用于时延估计、系统辨识、自适应滤波及阵处理等方面［1～2］。

在现代战争中，通信方便面临着日益严重的对抗威胁，而无源或被动探测技术是解决通信对抗威胁的有效途径之一，其中对接收信号进行高阶统计量的处理是一个重要的研究方向，它能辅助我方有效地提高区域防御系统的生存和反击能力，这也是近十几年来国内外研究的热点［3］。

高阶统计量能提供比功率谱更多的有用信息，能够有效地检测信号幅度以外的其他信息，这就具有明显的优点。高阶统计量作为非高斯信号处理的主要分析工具，不仅提供高阶相关信息，而且能够衡量随机序列偏离正态的程度，并对加性高斯噪声（白色或有色）不敏感。这些特点都非常有利于特征参数的提取［4］。

2 高阶统计量理论［5］

所谓高阶统计量，通常理解为高阶矩、高阶累积量以及它们的谱［6］。本文主要讨论高阶矩和高阶累积量，对它们的高阶矩谱和高阶累积量谱暂不作分析。我们首先将利用特征函数来定义高阶矩和高阶累积量，然后导出它们的相关性质，最后推导出高阶矩和高阶累积量之间的变换关系。

2.1 随机变量的特征函数

若随机变量的概率密度函数数为，则称：

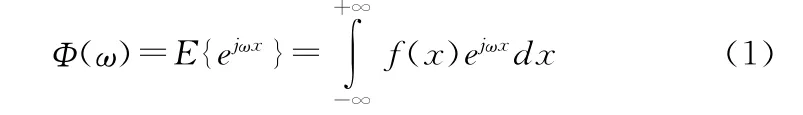
为x的第一特征函数。

设多维随机变量x1，x2，…，xn联合概率密度函数为f（x1，x2，…，xn），则n维随机变量的第一联合特征函数为

第二特征函数Ψ（ω）定义为第一特征函数的自然对数：

第二联和特征函数定义为第一联和特征函数的自然对数：

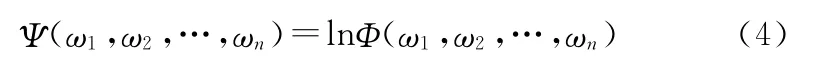
2.2 高阶矩和高阶累积量

随机变量的第一特征函数的阶矩mk为

通常将第一特征函数称为矩（Moment）生成函数。

随机变量x的第二特征函数Ψ（ω）的k阶累积量ck为

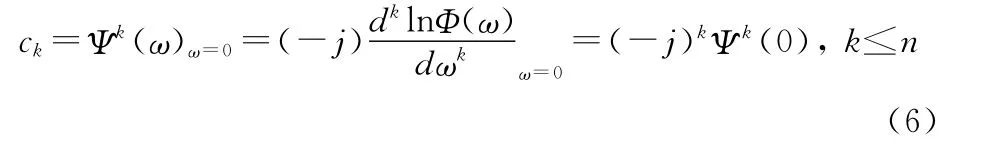
第二特征函数Ψ（ω）又称累积量（Cummlant）生成函数。

对随机变量的高阶矩和高阶累积量之定义加以推广，可以得出随机向量的高阶矩和高阶累积量。令X＝［x1，x2，…，xk］T是一随机向量。其特征函数为

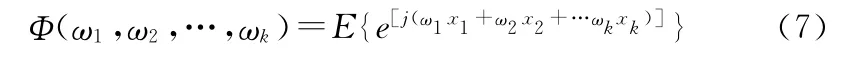
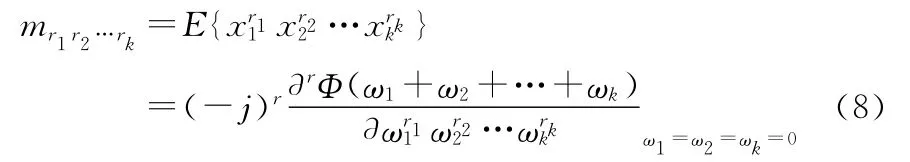
式（8）就是随机向量 X＝［x1，x2，…，xk］T的r阶矩的定义。类似的，随机向量的r阶累积量可用其累积量生成函数导出：

特别的，当取r1＝r2＝…rk＝1时，我们就可以得到k个随机变量的k阶矩（Moment）和k阶累积量（Cummlant），分别记作：

对于平稳随机过程的高阶矩和高阶累积量：设｛x（n）｝为零均值的k阶平稳随机过程，则该平稳随机过程的k阶矩mkx（τ1，…τk－1）定义为

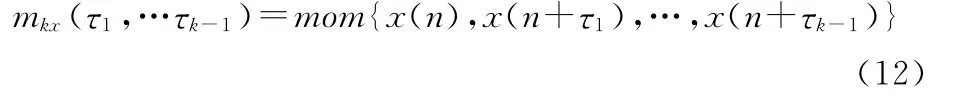
而k阶累积量ckx（τ1，…τk－1）定义为

3 通信信号高阶矩和高阶累计量计算

通过接收机，我们在不同的时间里对几个不同电台所发射的不同调制样式的短波通信信号进行了不同采样速率的接收。对接收到的信号进行去均值处理，去其直流成分，然后再对信号的高阶统计量（二阶、三阶、四阶）进行计算，并画出曲线图进行比较。

如果，x＝｛xi｝，i＝1，…，N 表示随机序列或信号的采样，则序列的矩为

其中E｛｝表示我们所熟悉的期望值的运算符；p（x）表示的是xn的概率密度函数。当采集得到的信号时间长度比较长时，认为是各态历经和平稳的［7］，同时进行了去均值处理，这样则采样信号的矩可由下式估计：

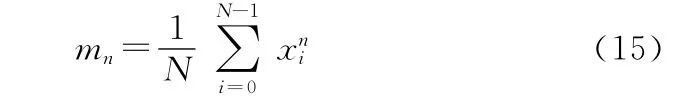
同样它的n阶累计量为

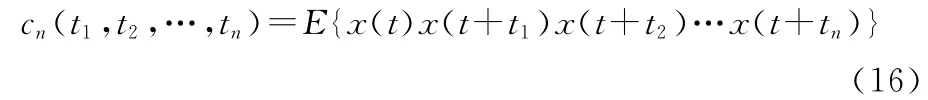
这样，前四个累计量可以用下式计算［8］：

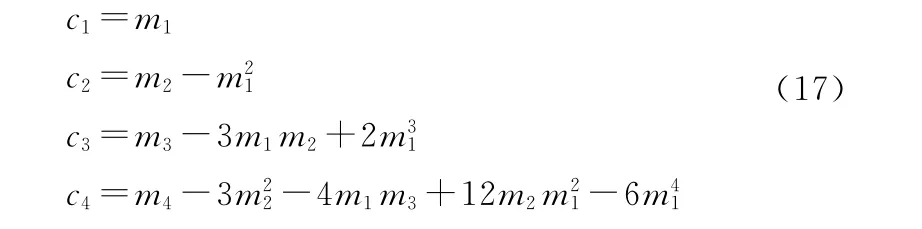
4 通信信号的高阶统计量特征分析

1）为了对同一电台、同一种调制样式信号（本文只对AM信号进行了试验分析）进行分析，我们在两个时间段内对AM666KHz电台的二阶矩和二阶累计量信号进行采样并通过Simulink［9～10］进行了仿真分析，如图1和图2，比较发现：测量的时间不同对同一电台AM信号的高阶统计量参数影响不大，它们的各阶统计量的波动范围都几乎在同一个很小的区间内，这反应了该电台的同一调制样式的信号高阶统计量参数的相对稳定性。

图1 AM666KHz电台不同采样速率的二阶矩值

图2 AM666KHz电台不同采样速率的二阶累积量值

2）现在我们对四个不同电台的AM信号进行了采样，它们是800KHz、864KHz、936KHz、1592.5KHz。发现它们各自的高阶统计量参数仍是较平稳的，不同的是各自的中心值和波动范围不同，以此我们可以将这些电台区分开。现将它们的各阶统计量画出，如图3～图8所示。

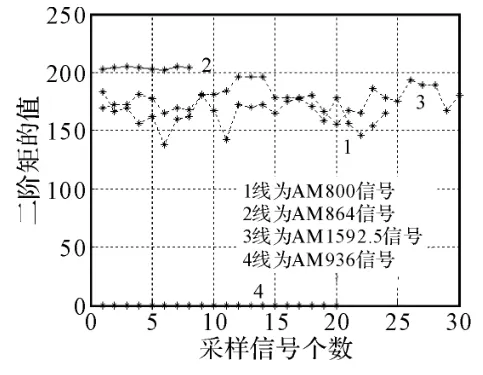
图3 四种电台AM信号的二阶矩值

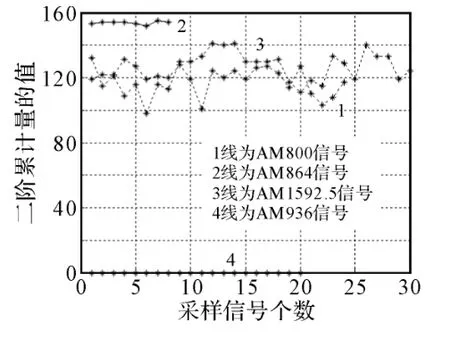
图4 四种电台AM信号的二阶累积量值

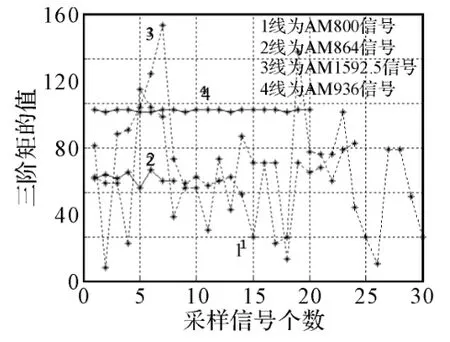
图5 四种电台AM信号的三阶矩值

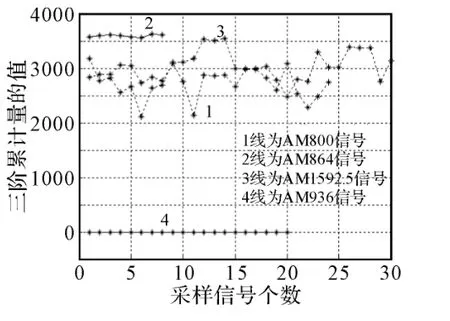
图6 四种电台AM信号的三阶累积量值

因此，对所有电台的高阶统计量参数计算、画曲线图后发现一个共同特点：对一定采样速率得到的采样信号，当对它们合并数目越多时（即新的采样信号的时间长度越长），信号的高阶统计量参数曲线越平稳，即参数越集中；而采样信号截的越短时（即新的采样信号的时间长度越短），信号的高阶统计量参数曲线越杂乱，抖动越大，即参数越分散。

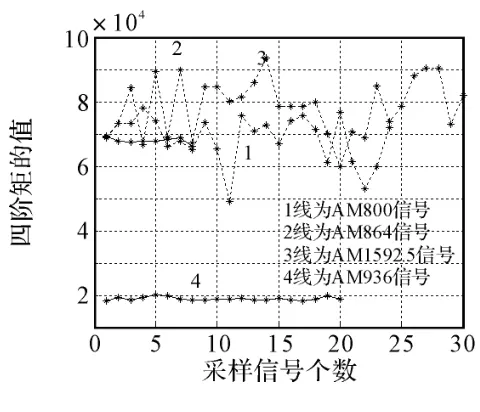
图7 四种电台AM信号的四阶矩值

图8 四种电台AM信号的四阶累积量值

3）通过实验结果的比较，我们得出了结论：在对同一电台的同一种调制样式（AM）信号在不同时间得到的高阶统计量的值是相对稳定的，区别也只是随机噪声带来的。这就为我们利用高阶统计量去识别这一信号的电台提供了实验依据。

同样，在对不同采样时间长度的比较中得到：采样时间越长，高阶统计量越稳定。对于这种现象，我们可以这样理解：因为我们在计算信号高阶统计量的时候，所采用的算法的前提条件是信号为各态历经和平稳的，而我们实际试验中采样的信号，由于噪声的影响和采样时间较短等因素，我们分析的信号是不太满足上述条件。但是如果采样信号时间越长，它就是越接近各态历经和平稳的，也就越满足前提条件。当合并信号，实际上是在加长采样信号的时间长度，而截短信号，是在减少采样信号时间。而同一电台发射的同一调制样式的信号基本是稳定的，这样当越接近条件时，对实验的效果越好，高阶统计量参数曲线也就越显得平稳。

5 结语

由于诸多因素的影响，对通信信号高阶统计量特征的研究还没有深入下去。这篇论文仅是对该方面的一个浅显的探索，只是其中的一小部分。对于下一步工作，可以从以下几个方面开展：

1）解决算法。由于计算信号高阶统计量的计算量太大，我们总是寻找简便的算法，这样就会出现不少的前提条件，如何使采样得到的信号更满足前提条件，这是需要考虑的；同时，对由于前提条件的不同而产生的高阶统计量的误差，还要进行分析校正。

2）信号样本。由于本文只着重对AM信号进行了分析，而没对其他的信号作进一步研究，这样所得到的参数还不充足。我们可以在对各种调制样式的信号采样时，不断改变采样信号的时间长度，看看在什么样的一个时间范围内，信号的高阶统计量可以进一步的稳定，这对信号识别很有借鉴价值。

3）高阶矩谱和高阶累积量谱。在这次分析中，只是针对于信号的时域分析，在对信号归一化（去均值）后利用算法进行的计算，而作为工程上所研究的高阶统计量还包括高阶矩谱和高阶累积量谱，即站在频谱的角度上对高阶统计量进行分析。高阶矩谱和高阶累积量谱会含有对提取信号特征更为有用的信息和规律。

［1］刘芳芳.通信系统中弱信号的高阶谱检测及特征分析［D］.哈尔滨：哈尔滨工程大学，2003：21－22.

［2］梁清泉.基于高阶统计量的波达方向估计技术的研究［D］.西安：西北工业大学，2002：13－14.

［3］武斌.基于高阶统计量的红外弱小目标检测［D］.西安：西安电子科技大学，2006：7－8.

［4］何海平，计时鸣.基于高阶统计量的信号分析与处理［J］.机电工程期刊，2003，20（5）：85－86.

［5］张晓云.高阶统计量在水雷目标特征提取中的应用［D］.哈尔滨：哈尔滨工程大学，2008：21－23.

［6］张贤达.现代信号处理［M］.北京：清华大学出版社，1995：377－379.

［7］樊昌信.通信原理［M］.北京：国防工业出版社，1999：23－25.

［8］Holly Moore.MATLAB实用教程［M］.北京：电子工业出版社，2010：105－112.

［9］Richard A.Poisel.通信电子战系统导论［M］.北京：电子工业出版社，2003：311－313.

［10］陈怀琛.吴大正，高西全.MATLAB及在电子信息课程中的应用［M］.第3版.北京：电子工业出版社，2001：304－307.