齿轮轮缘厚度对裂纹扩展路径的影响研究
刘双,朱如鹏,陆凤霞
(南京航空航天大学机电学院,江苏南京 210016)
0 引言
齿轮传动是直升机传动系统中最重要的一种传动[1]。齿轮传动在机器中应用很广泛,它既可以用来传递动力,也可以用来变换转速和旋转方向。通常齿轮设计需要平衡与优化成本,体积,寿命和可靠性等因素,齿轮传动的失效一般发生在轮齿上,而轮齿的折断一般发生在齿轮齿根部位,包括疲劳折断和过载折断[2]。随着我国直升机传动系统的发展,我们对齿轮的传动设计提出了更高的要求。近几十年来,国内和国外的专家学者们都从不同角度研究了齿轮齿根裂纹的断裂特性,但对齿根裂纹扩展研究较少,因此,从线弹性断裂力学的角度出发,结合商用有限元软件Abaqus来分析裂纹断裂过程的断裂力学特性;齿根的断裂特性受多种因素的影响,包括齿轮结构参数以及复杂外载,本文主要研究齿轮结构参数中的相同齿高下不同的轮缘厚度对裂纹扩展路径的影响。
1 轮齿折断的断裂力学特性分析
一个带有初始裂纹的齿轮,在交变载荷作用下,裂纹会缓慢扩展,当裂纹由初始长度扩展到临界尺寸时就会失稳破坏,这就是疲劳破坏。目前在工程中应用最为广泛的依然是1963年由Paris在实验基础上提出来的疲劳裂纹扩展公式-Paris公式,他建立了疲劳裂纹扩展速率与△k之间的关系:疲劳损伤在构件内逐渐积累,达到某一临界值时,形成初始裂纹;然后,在循环应力及环境的共同作用下,逐步扩展,即发生亚临界扩展;当裂纹长度达到临界裂纹长度时,难以承受载荷而断裂;通常把疲劳裂纹扩展分为三个阶段:微观裂纹扩展阶段,宏观裂纹扩展阶段,失稳扩展阶段;在工程实际应用中,一般主要以第二阶段作为疲劳裂纹扩展寿命的研究区域。
当带有裂纹的构件受到载荷作用时,裂纹端部的应力就会达到很大,理论上可以达到无限大,此时,常规的强度准则已经不适用,必须代之以应力强度因子来衡量材料的受载程度和极限状态。应力强度因子K是断裂力学里最为基本的参数,用来描述弹性裂纹尖端应力场强弱,它与外加载荷的大小和齿轮的几何形状有关。基本的断裂模式共有三种,张开型,滑开型,撕开型,其中的张开型裂纹是所有断裂中最危险的,也对裂纹扩展的影响最大。研究齿轮的断裂首先必须先研究裂纹端部的应力场,在任何应力下的裂尖应力场为:

其中:r为距裂纹尖端的距离,θ=arctan(x2/x1),KⅠ为张开型应力强度因子,KⅡ为滑开型应力强度因子,KⅢ为撕开型应力强度因子。对于二维裂纹,假定KⅢ等于0,则裂纹尖端的极应力表达式为:
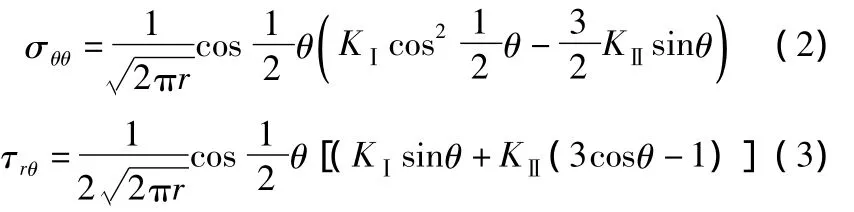
根据最大周向正应力理论提出的假设,当最大周向应力达到临界值时,裂纹开始沿着垂直于最大周向应力的方向扩展,裂纹扩展角度θ可以参考裂纹平面计算[4],裂纹扩展方向可跟据式(2)和式(3)中∂σθθ/∂θ=0 求得:

根据裂纹扩展角度,可以得出裂纹在循环载荷作用下不断往前扩展的扩展路径;在裂纹不断往前扩展的过程中,裂纹尖端各点的内应力也随着K增大而增大[5]。当k增大到某一临界值时,就能使裂纹尖端附近区域内的应力大到足已使材料分离,从而导致裂纹失稳扩展。这个临界值通常称为断裂韧性,即文中的KIc,这时,轮齿便会产生失稳扩展而很快断裂。
2 轮齿断裂有限元仿真
2.1 齿轮模型的建立
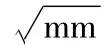

表1 齿轮基本参数

图1 齿轮模型
2.2 带有初始裂纹的齿轮模型的建立
定义一对齿轮副,大齿轮z=38,m=2.5,保证传动力矩180 T不变[8],通过接触啮合,分析得到小齿轮上载荷作用在单对齿啮合最高点[9],载荷为交变载荷,最大载荷为x方向为-209×6 N,y方向为655×6 N。在建模时,将初始裂纹位置置于齿轮上最大主应力处,也即齿轮齿根处,方向垂直于过度圆角[10]。齿根处初始裂纹模型如图2 所示[11],假定初始裂纹长度为 0.2 mm,在 Hypermesh 中对齿轮进行网格划分,定义为二阶网格。由于裂纹尖端的应力和应变是奇异的,因此在进行单元网格划分时,必须先在裂纹尖端位置定义奇异点,把裂纹尖端周围的网格单元上各条边中的节点移至靠裂纹尖端的1/4分点处[12]。划分好的带有初始裂纹的裂纹尖端网格如图2所示,图中粗线处为裂纹平面。
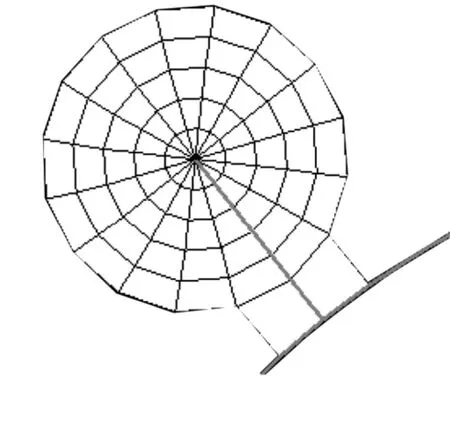
图2 裂纹尖端网格模型
网格划分好之后在abaqus中定义材料属性、加载载荷和边界条件,计算模型如图3所示。
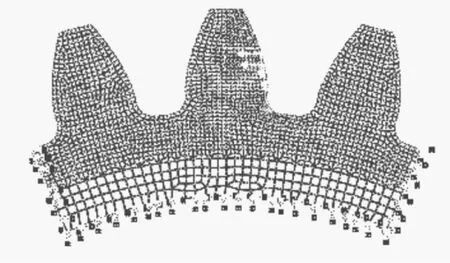
图3 加载后齿轮模型
模型生成后提交计算,计算中采用五围积分法,控制围积分输出,结果分别输出应力强度因子KI、KII。其中原始裂纹的初始裂纹平面通过两节点矢量测量得到。我们知道静载下的齿轮齿根裂纹是不会往前扩展,但齿轮在转动过程中,由于轮齿上所受的力为疲劳载荷,所以一旦产生初始裂纹,并且外力足够大,则裂纹就会不断往前扩展。在仿真计算过程中,给定裂纹扩展步长0.2 mm,当裂纹每扩展一步,分别求出裂纹尖端附近应力强度因子KI,KII,并代入式(4)求得裂纹开裂角θ0。根据计算得到的裂纹尖端的开裂角,把裂纹平面旋转角度θ0后沿着新的裂纹平面把裂纹往前推进,然后求出新的裂纹尖端附近的应力强度因子,模拟出第二阶段齿根裂纹扩展趋势,依次类推,可以分别得到第三,第四阶段的裂纹扩展路径。最后得出整个裂纹扩展路径如图4所示。

图4 裂纹扩展路径
通过齿轮齿根裂纹扩展仿真,可以预测裂纹的总体扩展方向,即沿着最大应力和齿轮强度薄弱的地方扩展[13]。这种裂纹扩展的模拟方法是建立在最大周向正应力理论的基础上的,为预测裂纹的扩展方向提供了很好的方法。
2.3 轮缘尺寸对裂纹扩展路径的影响
下面主要研究齿轮结构参数对裂纹路径的影响,主要考虑在相同齿数和模数下,不同的轮缘尺寸对根部裂纹应力强度因子以及裂纹扩展趋势的影响。假设在齿根附近相同的位置存在一条初始裂纹,其长度仍为0.2 mm。在计算过程中通过改变t/h的比值[14],使齿轮的全齿高和轮缘尺寸的比值发生变化,如图5所示。采用上述仿真分析方法模拟出两种情况下的裂纹扩展趋势,并计算得到每种情况下裂纹尖端的应力强度因子如表2所示。
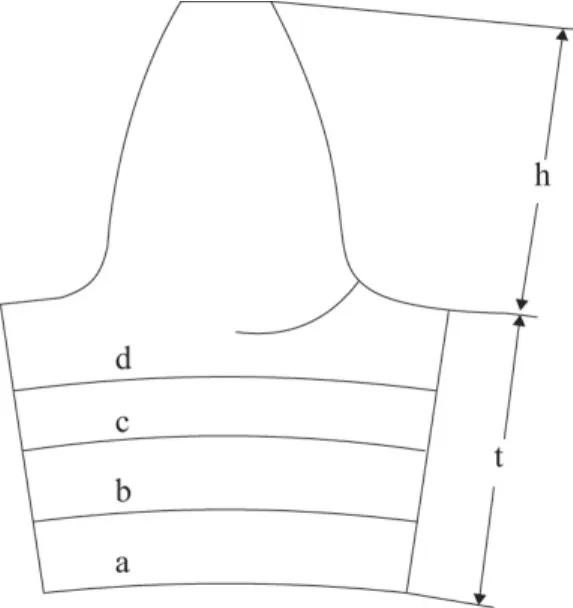
图5 齿轮轮缘尺寸变化

表2 裂纹尖端应力强度因子值

续表2
把求得的裂纹尖端应力强度因子值拟合成曲线如图6图7所示。

图6 裂纹长度与kⅠ关系图

图7 裂纹长度与kⅡ关系图
通过对不同轮缘尺寸下应力强度因子的曲线拟合,可以看出应力强度因子KI,KII在变化过程中,都是由小变大;在全齿高不变的情况下,在裂纹扩展的初始阶段,轮缘尺寸t越小,其裂纹尖端应力强度因子KI也越小,在裂纹不断往前扩展时,其增长速率越大;在整个裂纹扩展阶段,KI值远远大于KII值,因此在判断齿轮失效的过程中,可以忽略KII值对裂纹扩展的影响,仅以KIc作为齿轮失效的判据。
从上述分析可知,轮缘尺寸t越小,其裂纹尖端的应力强度因子增长速率越大,也即其应力强度因子值越容易接近该材料的断裂韧性,其轮齿越容易折断[15]。
根据Paris公式保守估计两种情况下的疲劳裂纹扩展速率,如图8所示,从图中可以看出轮缘尺寸t越小,其裂纹扩展速率越大。

图8 裂纹扩展速率
综合以上分析可知:假使根部出现裂纹,轮缘尺寸t越小的齿轮也越容易发生断裂。进行齿轮设计时,在考虑齿轮的使用寿命、质量、等因素的情况下,应该尽量增加轮缘尺寸t,或者增加齿轮根部的强度,从而消除齿轮结构参数对轮齿断裂的影响。
3 结语
裂纹从产生到最后失稳扩展中间会有一个稳定扩展阶段。本文提出了基于Abaqus的研究齿轮齿根裂纹扩展的方法,并根据最大周向正应力理论,结合一个具体的例子,分步模拟了齿根裂纹的扩展趋势,同时研究了不同的齿轮结构参数下裂纹的扩展趋势,保守估算出不同轮缘尺寸下裂纹的扩展速率,为齿轮的可靠性设计和抗断裂设计打下基础。
[1]尹双增.断裂损伤理论及应用[M].北京:清华大学出版社,1992.
[2]洪起超.工程断裂力学基础[M].上海:上海交通大学出版社,1986.
[3]David G.Lewicki.Gear crack propagation pathstudies-Guidelines for Ultra-Safe Design.NASA/TM—2001-211073.
[4]解德.断裂力学中的数值计算方法及工程应用[M].北京:科学出版社,2009.
[5]Panagiotis J.Papadakis.A numerical procedure for the determination of certain quantities related to the stress intensity factors in two-dimensional elasticity.Computer methods in applied mechanics and enginerring.122(1995):69-92.
[6]唐进元,周长江,吴运新.齿轮弯曲强度有限元分析精确建模的探讨[J].机械科学与技术,2004,23(10):1146-1150.
[7]J.Kramberger,M.Šraml,S.GlodeŽ.Computational model for the analysis of bending fatigue in gears.Computers and Structures 82(2004):2261-2269.
[8]江耕华.机械传动设计手册[M].北京:煤炭工业出版社,1982.
[9]杨生华.齿轮接触有限元分析[J].计算力学学报,2003(02):189-193.
[10]Shang DG,Yao WX,Wang DJ.A new approach to the determination of fatigue crack initiation size.Int J Fatigue.1998;20:68 3-7.
[11]B.Alfredsson,M.Olsson* .Initiation and growth of standing contactfatigue cracks. Engineering fracturemechanics.65(2000):89-106.
[12]王慰军.基于abaqus的扩展仿真软件及应用[A].杭州:浙江大学硕士学位论文,2006.
[13]Ales Belsak,Joze Flasker.Detecting cracks in the tooth root of gears.Engineering Failure Analysis 14(2007)1466–1475.
[14]Michele Ciavarella,Giuseppe Demelio.Numerical methods for optimization of specific sliding,stress concentration and fatigue life of gears.International Journal of Fatigue 21(1999):456-474.
[15]曾竞龙.结构疲劳裂纹产生与扩展的计算模拟[D].武汉:武汉理工大学,2005.5.

