复合材料起落架舱门结构优化设计

徐子澎，王志瑾

（南京航空航天大学航空宇航学院，江苏南京 210016）

0 引言

复合材料与常规的金属材料性比具有优良的力学性能，在质量相当的情形下复合材料承载能力和刚度更大，并且具有很强的可设计性，已经被广泛应用于先进飞机结构。其中复合材料夹芯结构主要是由两块薄而强硬的复合材料层合面板及比重轻、相对面板较厚、承载能力相对较弱的芯体通过粘接剂粘在一起，可以充分发挥芯子低密度的特点以加大构件厚度，使结构达到减重的目的并且大大增大夹层面板截面的惯性矩和弯曲刚度。因而有利于夹层结构提高屈曲载荷与固有频率、减小变形;有利于隔音、隔热和减振，且光滑的表面使其具有了良好的空气动力学性能。并且复合材料蜂窝结构增加了许多可设计变量，如纤维方向角、铺层厚度、夹芯厚度、夹芯规格等，有较大的结构优化潜力。由于这些优异的力学性能和物理性能使得世界各国对这种材料的研发越来越重视。

蜂窝是一种结构型材料，现有通用有限元软件中进行数值计算时，因此蜂窝芯子不能直接给定材料属性，需要采用等效理论计算［1］。本文以起落架舱门蜂窝夹层结构为例，先对蜂窝夹层结构的蜂窝芯子使用三明治夹芯理论进行等效参数计算，并基于有限元程序ANSYS中建立起落架舱门复合材料蜂窝夹层结构参数化模型，选取面板铺层板各方向铺层厚度以及蜂窝夹芯高度为设计变量，以铺层板、蜂窝夹芯的强度、结构稳定性及结构刚度作为约束函数，以结构质量为目标函数对飞机起落架舱门进行优化设计分析。

1 蜂窝夹层板芯子等效计算

由于蜂窝是一种结构型材料，ANSYS等通用有限元程序中没有蜂窝结构单元，只能采用三维有限元方法进行模拟分析，但是计算量巨大，对于一个较为复杂的结构进行分析时，会耗费大量时间。在此基础上，研究者在理论上找出蜂窝夹芯结构等效力学模型，用此模型代替原来的结构，可以达到较高的精度。其中三明治夹芯板理论是对蜂窝夹芯进行等效的一种有效、精确的方法［2］，假定芯层能抵抗横向剪切变形并且具有一定的面内刚度;上、下蒙皮层服从Kirchhoff假设，并忽略其抵抗横向剪应力的能力，将蜂窝芯层等效为均质的厚度不变的正交异性层。正六边形蜂窝胞元示意图如图1所示。根据文献［3］其等效参数为式（1）。式中:x、y表示板平面上两正交方向，z表示蜂窝高度方向;ES为夹芯材料的工程常数;GS夹芯材料的剪切模量;l、t分别为蜂窝胞元壁板的长度和厚度;γ为修正系数，取决于工艺，一般取0.4 ～0.6，文中取0.4。

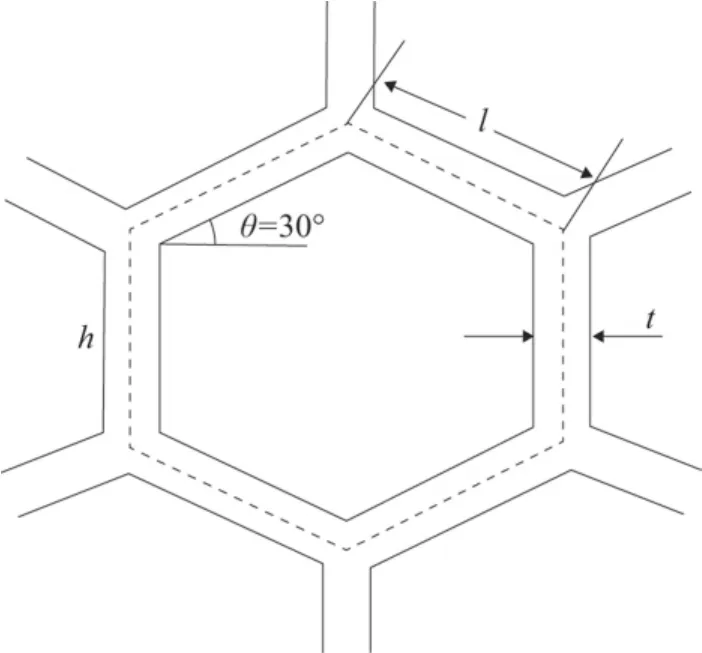
图1 正六边形蜂窝胞元示意图

中蜂窝芯子采用的规格是NRH-3-64，已知芯材壁厚为0.05 mm，芯子边长为3 mm。蜂窝芯子弹性常数以及力学性能见表1。

表1 蜂窝芯子弹性常数

2 起落架舱门有限元模型

基于有限元程序ANSYS建立复合材料起落架舱门结构参数化模型，起落架舱门几何尺寸:1 787 mm×406 mm。为了防止在边界条件处产生应力集中，在结构设计阶段在铰链及摇臂支撑点处区域增加加强肋，肋的铺层参数不作为优化参数。有限元模型中，上、下面板和肋选用壳单元，考虑到肋与面板的中性面不在同一面上，对肋与面板重叠处进行截面偏置;上、下面板为T700/BA9916的复合材料层合面板，单层板厚度为0.15 mm，其材料弹性常数和强度参数见表2，选择蔡吴失效准则为面板材料强度判据准则，上、下面板初始铺层为对称铺层即:［45°/0°/-45°/90°］3s。等效蜂窝芯层选用实体单元，蜂窝夹芯的初始高度为39 mm，蜂窝材料参数为基于三明治夹芯理论等效后的材料参数见表1。在A、B、C铰链处起落架舱门可以围绕总体坐标系下x轴转动，即放松该处节点rx自由度;在操纵摇臂支撑点d处简化为固支，约束接头处节点所有自由度，如图2所示;在上面板施加气动载荷0.013 5 MPa。

表2 面板T700/BA9916材料弹性常数

图2 起落架舱门有限元模型

3 优化设计

为了适应制造条件，也为了简化优化设计/分析与工艺，单层铺层角直接规定为几种复合材料设计和工艺要求的四种铺层方向:0°/90°/-45°/45°，因此中铺层角度不作为设计变量，只选择铺层厚度为设计变量。由于制造条件的限制，对于所求出的优化值，最终要圆整到生产容许的数值，在设置参数过程中，考虑到这一事实，首先设置参数实数A，再使用ANSYS中取整函数NINT（），因此在优化过程中，选取A为优化参数，在优化过程中参数N=NINT（A）会自动圆整，并直接参数化赋给单层板厚度，最后得到的N即为真实结构铺层厚度并能直接得到蜂窝夹层结构质量，无须进行圆整。

设计变量:上面板四个铺层方向的厚度（UPT-45°/UPT45°/UPT0°/UPT90°）;下面板四个铺层方向的厚 度（DOWNT-45°/DOWNT45°/DOWNT0°/DOWNT90°）;蜂窝夹芯的高度H。

约束条件:1）面板和肋强度校核［4］:蔡吴失效因子＜1;

2）蜂窝芯子强度校核［4，5，7］:

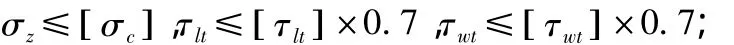
3）刚度约束:结构在承受局部气动载荷时的最大位移≤5 mm;

4）结构不发生失稳。

其中，[σc]，[τlt]，[τwt]分别是蜂窝芯子的压缩强度，纵向和横向剪切强度。

设计目标:复合材料起落架舱门结构质量最轻。

4 起落架舱门优化结果分析

图3 优化流程

起落架舱门夹层结构的上、下面板初始设计铺层均为:［45°/0°/-45°/90°］3s;蜂窝夹芯原始厚度为 39 mm;舱门结构中局部加强肋初始铺层为［45/-45/0/45/90/-45/0/45/90/-45］s，结构初始质量为 12.8 kg。根据图3优化流程，基于ANSYS建立复合材料起落架舱门参数化模型，静力求解后读取面板各铺层单元的蔡吴失效因子，设置夹芯材料的失效准则;屈曲分析后读取失稳因子。在优化模块中，首先选用子问题逼近法进行第一轮优化，得到较粗略的优化结果，此时可以在这个结果的基础上再进行一阶梯度优化，这样可以得到更精确的解，并能减少优化时间。选用一阶优化方法，并给定义设计变量、状态变量、目标函数的程序语句都加上公差，防止其提前收敛，进行进一步逼近最优解。得到优化参数后，上面板铺层为:［45°/45°/0°/0°/-45°/90°/90°］s，下 面 板 铺 层 为 ［45°/0°/-45°/90°］2s，蜂窝夹芯厚度为 45.3 mm，质量为 8.4 kg，满足设计要求。优化结果进行静力分析位移变形图见图4，最大变形量3.6 mm，没有超过刚度约束值5 mm;一阶失稳因子＞1，满足结构稳定性要求。

图4 位移变形云图

5 结论

基于ANSYS有限元程序建立复合材料起落架舱门蜂窝夹层结构参数化有限元模型，首先基于三明治夹芯理论将蜂窝夹层等效为均质的厚度不变的正交异性层，选择面板各铺层厚度与蜂窝夹芯高度为设计变量，选择面板各铺层强度和蜂窝强度、结构稳定性及结构刚度为约束函数，以结构质量为目标函数，基于ANSYS优化模块首先选用子问题逼近（零阶）优化方法对结构进行初步优化，然后选用一阶梯度优化方法进行进一步优化设计，对起落架舱门减重效果较为理想。本文中的蜂窝夹芯芯子只考虑一种规格，可以进一步考虑在蜂窝夹层结构优化分析过程中，加入对蜂窝芯子规格选型优化的部分，做进一步深入的研究。

［1］雷江利.复合材料夹层结构优化设计方法研究［D］.西安:西北工业大学，2006.

［2］张铁亮，丁运亮，金海波.蜂窝夹层板结构等效模型比较分析［J］.应用力学学报，2011，28（3）:275-282.

［3］富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31（1）:113-118.

［4］中国航空研究院.复合材料设计手册［M］.北京:航空工业出版社，2001.

［5］修英姝，崔德刚.复合材料蜂窝夹层结构的优化设计［J］.北京航空航天大学学报，2004，30（9）:855-858.

［6］杨乃宾，章怡宁.复合材料飞机结构设计［M］.北京:航空工业出版社，2002.

［7］Ding Y.Optimum design of sandwich constructions［J］.Computers＆ Structures.1987，25（1）:51268.