基于接触应力的圆柱滚子轴承疲劳寿命分析

邱江，朱如鹏，陆凤霞，靳广虎

（南京航空航天大学，江苏南京 210016）

0 引言

圆柱滚子轴承一般用于载荷较大的场合，与同尺寸球轴承相比，圆柱滚子轴承通常具有更高的刚性和更好的抗疲劳性［1］。轴承的疲劳寿命是轴承设计与使用中的重要参照因素，对于滚子轴承来说主要的失效形式是接触疲劳，但是由于金属材料的接触应力一般较大，要进行零部件全尺寸的接触疲劳试验耗时会相当长。另外，大量实验数据表明，滚动轴承在型号、转速等外在条件完全一致的状况下，其实验寿命结果最大值与最小值相差甚远，即寿命的离散性很大［2］。因此要想得出一组可靠的数据，必须开展大量的疲劳实验，这样的费用是高昂的。因此，理论计算方法在获得轴承接触疲劳寿命在实际生产过程中就显得非常重要。

轴承的经典疲劳寿命计算方法是建立在Lundburg和Palmgren等人的经验基础上。大量的生产实践证明，这种方法是较为可靠的。但在直升机疲劳定寿中，目前国内外对传动系统零部件的疲劳寿命评估普遍采用的是名义应力法的有限寿命设计［3］。其设计基本思想是从材料的S－N曲线出发，再考虑可靠度、应力集中系数等多种影响因素;最后结合应力值求出疲劳寿命值［4］。本文基于接触应力对圆柱滚子轴承的疲劳寿命进行了计算，并将计算结果与经典疲劳寿命理论结果进行了比较。证明这种方法是可行且较为可靠的，为圆柱滚子轴承的疲劳寿命特别是针对直升机传动系统轴承部件的疲劳寿命评估提供了一定的依据。

1 圆柱滚子轴承接触疲劳寿命分析的基本原理

1.1 L－P疲劳寿命计算理论

轴承疲劳寿命的计算方法建立在Lundburg和Palmgren的理论基础上。对于圆柱滚子轴承，在法向载荷Q作用下，滚子与滚道线接触的寿命为:

式中，滚道额定接触动载荷Qc为:

式中，D为滚子直径;l为滚子有效长度;Z为滚子数;γ为Dcosα/dm;α为接触角;dm为节圆直径;λ是随滚子引导方式而变化的系数。

圆柱滚子轴承的寿命由内、外环疲劳寿命的交集表示

式中，Lμ为滚子与内滚道接触寿命;Lν为滚子与外滚道接触寿命;对于线接触轴承，威布尔斜率e取9/8。

建立在Lundburg和Palmgren的疲劳寿命理论是对轴承理论的重要发展。但是，T.A.Harris同时也指出了它存在的两个主要缺点［1］:

a）这种计算轴承表面滚动接触疲劳寿命的方法不能与其他工程结构疲劳计算方法相关联，即不具备通用性。

b）该种方法得出的结果不论外加载荷是多大，轴承的疲劳寿命总是有限的。然而实验证明经过标准设计和采用高品质钢材制造的轴承其无限长的疲劳寿命是实际存在的。

因此，该公式不能说明无限疲劳寿命，也就不完全适合结构疲劳预测。在超出试验条件时，必须采用一些经验寿命调整系数来进行改进。

1.2 滚子法向载荷和接触应力的计算

由于滚动体的轨道速度和绕自身轴线的转动，在滚动体和滚道之间会产生动力载荷。这种载荷在中、低速运转下，与作用在轴承上的径向载荷相比是很小的，因此在轴承寿命的经验计算公式中转速对结果并没有影响;但对于高转速来说，滚动体的动力载荷即离心力和陀螺力矩将改变作用载荷在滚子之间的分布。在直升机主减速器的第一级传动中，由于输入轴的转速较大，因此在主减速器的第一级传动中通常采用高速轴承。因此，在这里有必要对轴承受到的法向载荷进行详细的求解计算。

在不计摩擦力矩和油膜作用的情况下，承受径向载荷Fc的高速圆柱滚子轴承的滚子受载如图1所示。

图1 角位置ψj处的滚子载荷

图中，Qij和Qoj分别为在任意角位置ψj处内、外滚道与滚子间的法向作用载荷;Fc为滚子受到的离心力;考虑力的平衡有:

式中，K为载荷位移系数;δ为接触变形;对于以速度nm绕轴承轴线转动的钢制滚子，离心力Fc可表示为:

因为δrj=δij+δoj，式（4）可以被改写为以下形式:

从受载轴承的几何关系可以确定任意方位角ψj处的总径向压缩变形为:

式中，Pd为径向游隙，将式（8）代入式（7），可以得到:

另外在轴承的径向载荷作用方向，同样满足力平衡要求:

联立式（9）和式（10）可求解由Z+1个方程构成的非线性方程组。采用Quasi－Newton法对平衡方程构成的非线性方程组进行迭代求解。

图2 高速圆柱滚子轴承载荷计算流程图

由于基于接触应力法只考虑最大应力处的疲劳损伤，因此载荷Q应为轴承滚动体受到的最大载荷Qmax，即瞬时处于位置角ψ=0时的滚子与滚道间的载荷。

根据Hertz接触应力理论，对于理想线接触的两圆柱体，其最大接触应力σmax和接触椭圆短半轴b为:

式中，∑ρ为曲率和函数;ξ为泊松比;E为弹性模量。

1.3 疲劳寿命曲线的确立

结构的疲劳特性通常采用S－N曲线来描述，即结构承受的载荷与其在该载荷下发生疲劳破坏所经历的循环次数的关系曲线［5］。本文选用直升机设计中常用的三参数幂函数，即

式中，C和m为材料的常数，S0为材料的疲劳极限，对式（13）两边同时取对数有:

令A0=lgC，B0= －m，Y=lgN和X=lg（S－S0）代入式（14）中，可以得到线性方程:

圆柱滚子轴承的材料选取GCr15轴承钢，查取《机械工程材料性能数据手册》，其接触疲劳性能数据见表1所示。

表1 GCr15轴承钢接触疲劳性能数据

GCr15轴承钢的接触疲劳极限为2 000 MPa，在线性坐标系下拟合可以得到存活率为50%、90%及99%时对应参数C和m的值，从而得到不同存活率下对应的S－N曲线方程。

2 接触疲劳寿命实例分析与比较

圆柱滚子轴承在承受径向载荷为15 000 N，材料为GCr15，轴承的主要参数如表2所示。

表2 圆柱滚子轴承的主要参数

改变圆柱滚子轴承的参数，通过建立在Lundburg和Palmgren的经典疲劳寿命理论得到的结果与基于接触应力得到的疲劳寿命结果进行比较。

图3至图5是转速在2 000 r/min情况下，改变圆柱滚子轴承设计参数得到的疲劳寿命。不难发现基于接触应力得到的疲劳寿命与经典理论方法得到的疲劳寿命在趋势上完全一致，且数值上也较符合，这充分说明了该方法的可行性。另外，在轴承设计参数趋于安全的情况下，基于接触应力得到的疲劳寿命值变化更为明显，即随着轴承设计安全性的增强其寿命是趋于无限寿命的。这弥补了经典理论的不足。

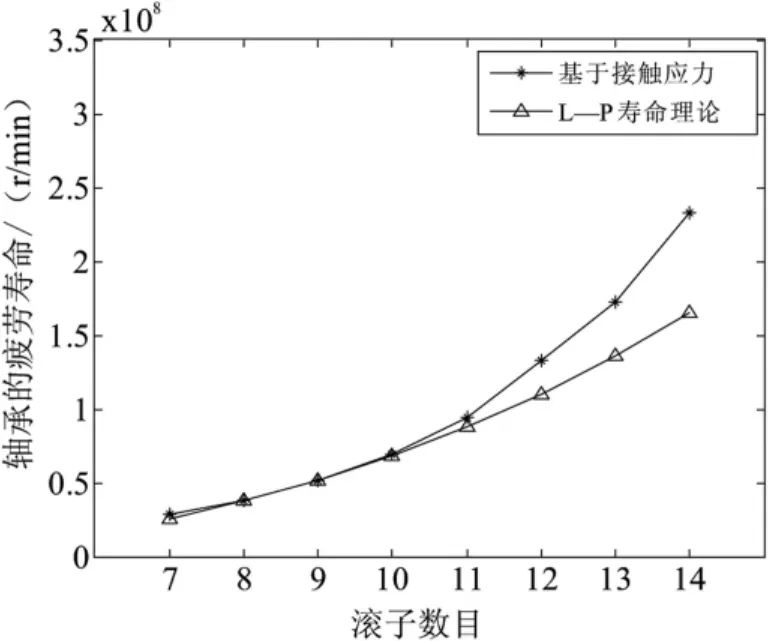
图3 滚子数目对轴承疲劳寿命的影响

图4 径向力对轴承疲劳寿命的影响

图5 径向游隙对轴承疲劳寿命的影响

图6是基于接触应力和经典疲劳寿命法分别随转速变化的疲劳寿命趋势图。可以发现:基于接触应力得到的寿命值随着转速的增大，变化较经典理论方法更为明显。这是因为接触应力法在计算寿命时只考虑最大应力处的疲劳损伤状况，而经典理论方法考虑的是内、外滚道与滚子间的载荷综合状况，这也是其变化趋于平缓的主要原因。由此可见，基于接触应力法在针对高转速圆柱滚子轴承疲劳寿命的计算中，其结果是趋于保守的，这也符合该方法偏于安全的特征。正是因为这样的特点，使得其在航空附件的疲劳寿命评估中得到了广泛的运用。

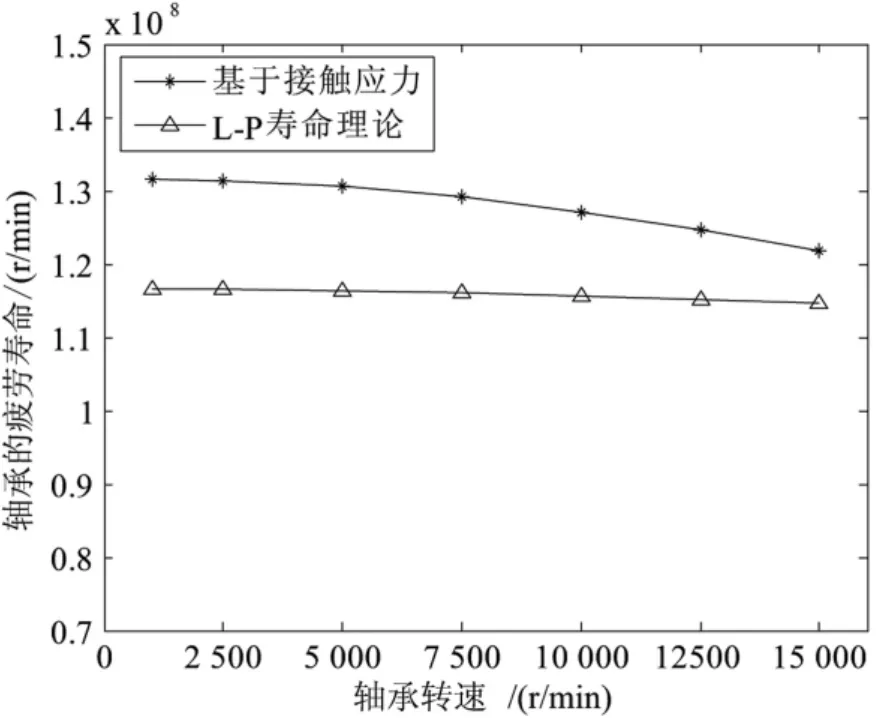
图6 轴承转速对轴承疲劳寿命的影响

3 结论

本文应用航空零部件疲劳定寿中常用的名义应力法，基于轴承的接触应力对圆柱滚子轴承的疲劳寿命进行了预估算。考虑离心力等因素对轴承载荷的影响，并采用三参数幂函数方程计算得到了轴承的疲劳寿命。其结果与建立在Lundburg和Palmgren的经典寿命计算结果相符。充分说明了该理论运用于圆柱滚子轴承寿命计算的合理性。相较于经典理论，基于接触应力得到的轴承疲劳寿命，在计算过程中更能体现出材料对疲劳寿命的影响，且在材料强度大或设计趋于安全的情况下能够达到无限寿命，从而克服了经典理论无法获得无限寿命的不足。

［1］Harris T A，M N Kotzalas.滚动轴承分析［M］.北京:机械工业出版社，2009.

［2］徐小平，何复超.滚动轴承疲劳寿命P－S－N曲线［J］.现代机械，1995（9）:1-3.

［3］ Liard F.Helicopter Fatigue Design Guide-AGARDograph，No292，1987.

［4］赵少汴，王忠保.疲劳设计［M］.北京:机械工业出版社，1992.

［5］穆志涛，曾本银.直升机结构疲劳［M］.北京:国防工业出版社，2009.