GPU加速的傅里叶变换轮廓术并行计算方法

赵小敏，周波，刘春媛，陶金

（黑龙江科技学院，黑龙江哈尔滨 150027）

0 引言

随着计算机技术，光学和光电子技术的迅速发展，物体三维面形测量［1］成为现代光学计量的一个重要分支，其以非接触、高精度、易于测量［2］等优势得到广泛应用。在主动三维面形测量技术中，傅里叶变换轮廓术（fourier transform profilometry）［3］只需要一帧变形条纹图就能恢复出物体的三维面形，但当图像尺寸较大时，其计算量较大，使用CPU或DSP串行处理图像数据速度慢、效率低［4］，难以实现对动态物体的实时测量。值得庆幸的是，在利用傅里叶变换提取相位时其待处理的数据和已处理的数据是相对独立的图像像素，具有极高的计算密度，适于通过多线程运行相同的程序计算，所以并行处理是提高其计算速度的最佳解决方案。

图形处理器（GPU）［5］是一种高度并行化、多线程、多核的处理器，专为计算密集型和高度并行化的计算而设计，具有相当高的内存带宽和大量的执行单元，为图形处理以外的通用计算提供了良好的运行平台。统一计算设备架构（CUDA）［6］是NVIDIA推出的GPU通用计算产品，能够有效利用GPU强劲的处理能力和巨大的存储器带宽进行图形渲染以外的计算，完全扭转了传统GPU通用性差这一困难局面，使得GPU打破图形语言的局限成为真正的并行数据处理器。本文基于CUDA平台实现了傅里叶变换轮廓术的GPU加速，利用CUDA并发执行的优点，将计算过程中计算密度较大且可以并行计算的工作在GPU上完成，实现了CPU与GPU的协同工作，因此，在保证图像品质的情况下，提高了傅里叶变换轮廓术的计算速度，为实现实时三维测量奠定了基础。

1 傅里叶变换轮廓术

傅里叶变换轮廓术，是通过对获取的光栅图像进行傅里叶变换、滤波和逆傅里叶变换提取出相位信息，由相位信息恢复出物体的三维面形高度分布［7］。

1.1 基本原理

图1所示是傅里叶变换轮廓术的系统光路结构图［8］，Ep和Ec分别是投影系统和成像系统的光轴，两光轴与参考平面xoy相交。l0是成像系统到参考平面的距离，d是成像系统与投影系统之间的距离。

按照图1中所示的坐标系，将垂直于x轴的光栅投影到参考平面时，CCD相机获取的成像条纹记为:

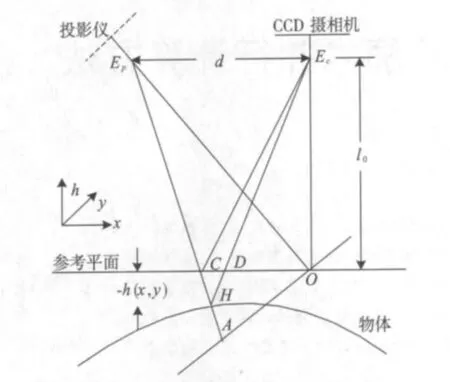
图1 傅里叶变换轮廓术的系统光路结构图

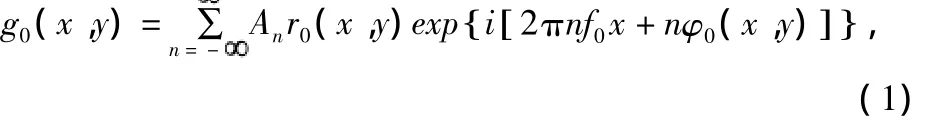
其中，An代表傅里叶级数的系数;r0（x，y）是参考平面上的非均匀反射率分布函数;f0为光栅像的空间频率;φ0是参考平面上的相位分布。在结构参数相同的条件下，将该光栅投影到待测物体表面上，CCD相机得到的变形条纹分布为:

r（x，y）是物体表面非均匀反射率分布函数;φ（x，y）是由于物体表面高度变化而引起的相位调制。为了获得由物体高度引起的相位变化Δφ（x，y），分别对式（1）和式（2）进行傅里叶变换，经过滤波获取所需要的相位信息的基频分量，再对基频分量进行逆傅里叶变换，得到的复分布表示为:

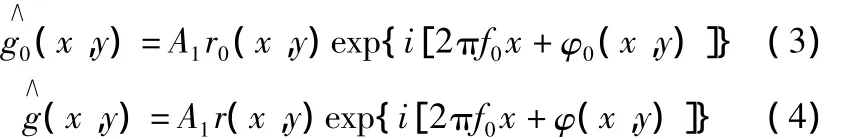
由物体高度分布引起的相位变化为:

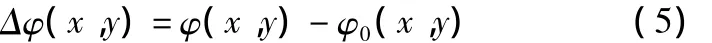
由于物体的高度信息被编码在相位φ（x，y）中，而Δφ（x，y）对应待测物体的真实高度分布h（x，y），因此，只需要求出相位差Δφ（x，y）并将其恢复为连续相位，再利用相位与高度之间的映射关系，即可计算出物体的三维面形。

1.2 物体表面相位的计算

对滤波后的基频分量进行逆傅里叶变换以后，获得条纹图像的复分布式（3）和式（4），将式（3）和式（4）的共轭相乘，得:

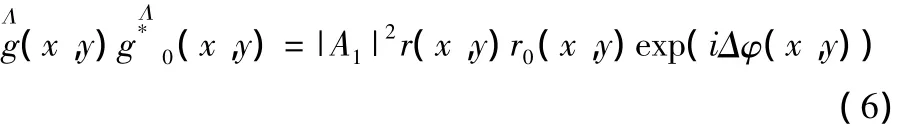
其中，“* ”表示共轭，|A1|2，r（x，y），r0（x，y），Δφ（x，y）均为实函数，则变形条纹相对于参考平面的相位差为:

1.3 相位－高度的转换

系统光路结构如图1所示，投影在参考平面上的光栅条纹是等周期分布的，其频率为f0，相位分布φ（x，y）是坐标 x的线性函数［9］，记为:

以参考平面上O点为原点，C点的相位为:

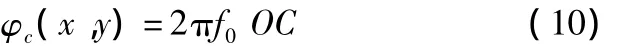
被测三维表面H点的相位对应于参考平面上D点的相位，即:

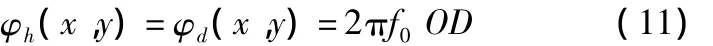
因此，由物体高度引起的相位调制Δφ（x，y）为:

由△HCD与△HEpEc相似，可得:

由式（12）和式（13），得:

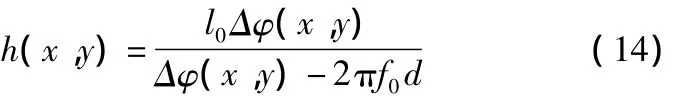
即可恢复出物体的三维面形高度分布。

2 GPU加速

2.1 GPU高性能运算模型CUDA

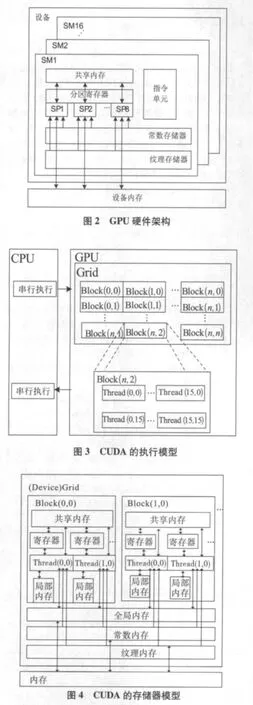
CUDA是NVIDIA公司发布的用于GPU通用计算的开发环境和软件体系［10］，利用GPU强大的运算能力，可实现并行处理。GPU的硬件架构以NVIDIA Quadro FX 1700为例，如图2所示，该GPU由16个SM（流多处理器）组成，每个SM包含8个SP（流处理器）、常量缓存和纹理缓存以及其他单元。在CUDA架构下［11］，GPU作为设备执行高度线程化的并行处理任务，运行在GPU上的函数称为 Kernel，其线程被组织成三层结构，即:线程网格（grid）、线程块（block）和线程（thread）。CUDA的执行模型如图3所示［12］，Thread以Block为单位分配到 SM，SM采用Warp管理线程的执行，同一Block中连续的32个线程组成一个Warp。Thread在执行时将会访问到处于多个不同存储空间中的数据［13-15］，如图4所示，Grid中的所有线程可访问全局存储器、常数存储器、纹理存储器，同一Block中的线程可访问同一共享内存，每个Thread拥有私有的寄存器和局部存储器。

2.2 GPU并行计算的实现

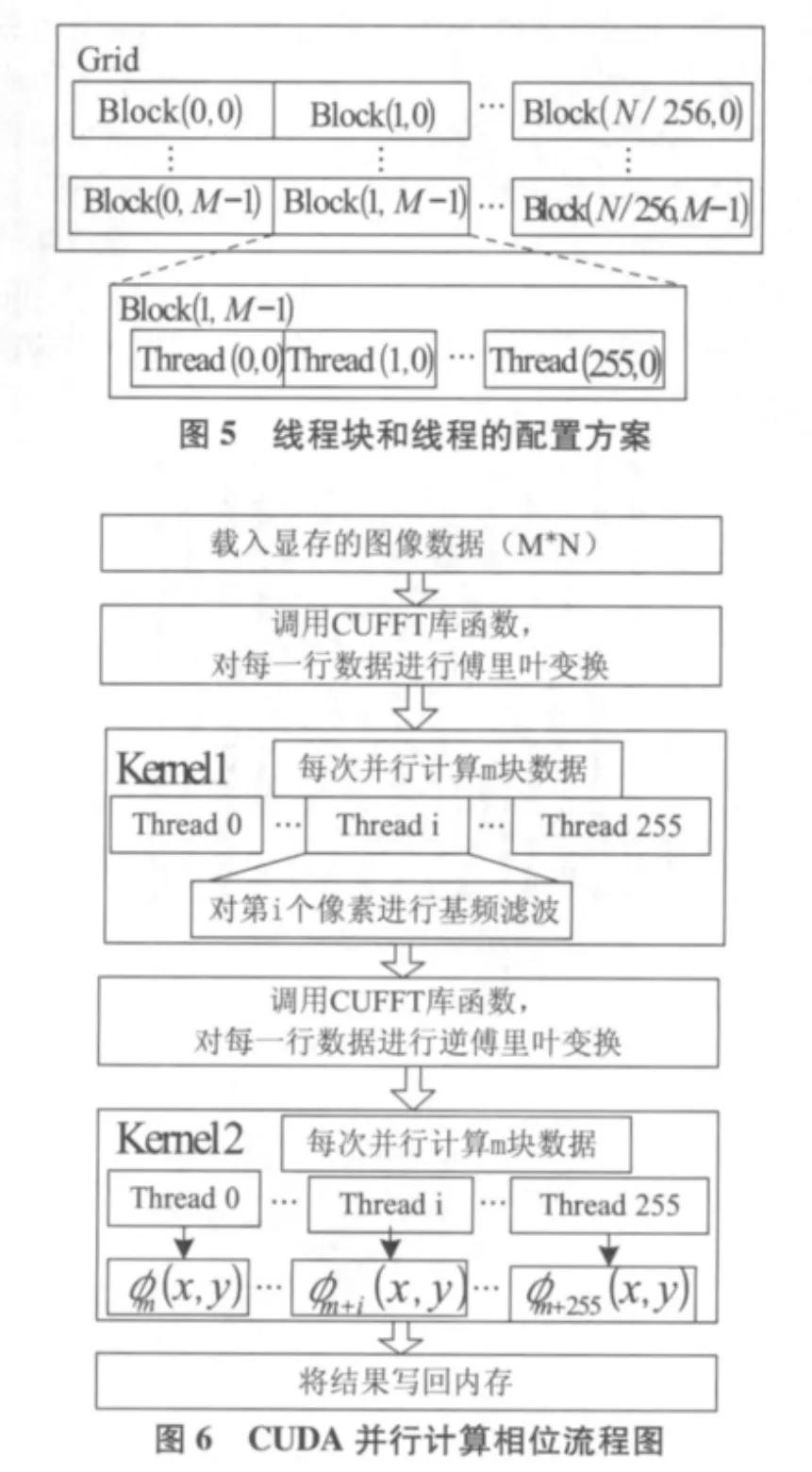
傅里叶变换轮廓术由多个不同的处理步骤组成，应考虑各部分的计算复杂度，分别采用合适的处理平台，使CPU与GPU协同工作，以达到最优的处理速度。由于在相位展开时存在大量的分支语句，不适合GPU实现，而在提取相位部分需处理全部的像素且计算规整，因此，本文的GPU加速主要针对提取相位部分。

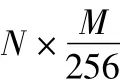
3 实验结果及分析

采用Nvidia公司的Quadro FX 1700显卡作为GPU硬件，它集成了128个流处理器，板载512 MB显存;CPU为Intel Core－4 E5420@2.5 GHz;软件开发工具为 Microsoft visual studio 2005。为验证本文提出算法的有效性，使用了多组大小不同的计算机模拟条纹图进行了验证，并与在CPU上使用fftw库算法进行了比较，表1是在CPU与GPU上处理时间的对比结果。

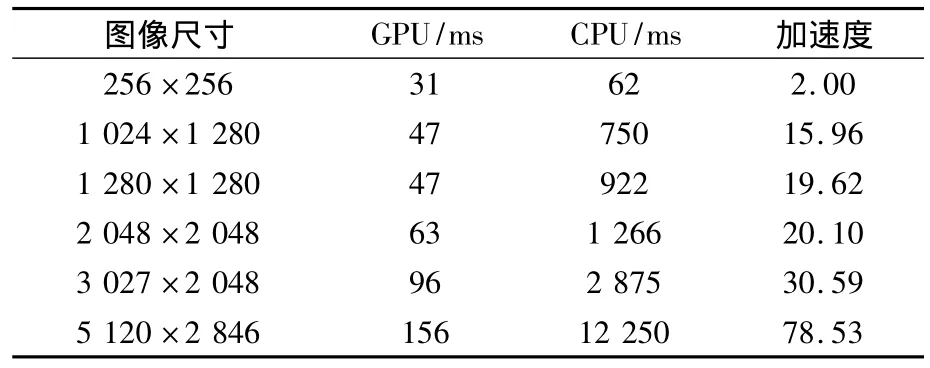
表1 GPU与CPU的处理效率对比

从表1可以看出，随着图像尺寸增大，GPU较CPU的相对运行时间明显偏少，并行计算优势显现。影响GPU整体性能的原因有两个:1）对于小尺寸的图像而言，其CPU计算循环次数较少而且CPU主频高于GPU和单线程计算能力突出，制约了GPU加速性能;2）由于GPU的加速处理时间包括数据在CPU和GPU之间传输的时间，当图像像素数目增多时，计算量随之增大，计算时间占总处理时间的比例越大，因此，GPU强大的并行执行能力明显体现。为验证本算法的精度，选取256×256的模拟条纹图如图7（a）所示，分别在CPU与GPU上进行处理，处理后的结果如图7（b），（c）所示，可以看出GPU在提高计算速度的同时没有产生额外的计算误差。由此可见，GPU并行运算在保证图像处理效果和低成本的前提下，有着很高的并行效率。

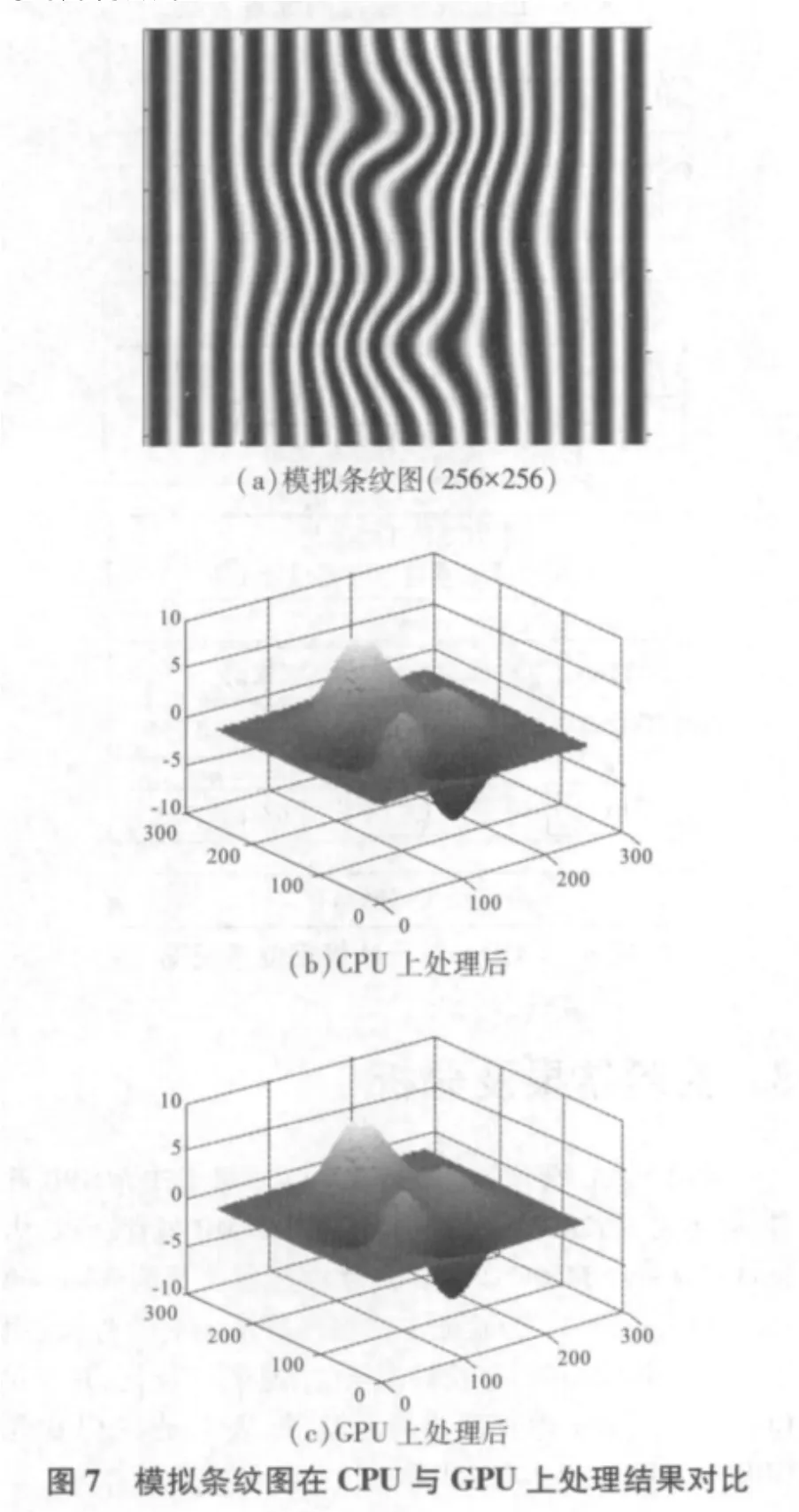
4 结论

针对在傅里叶变换轮廓术中相位计算耗时的问题，本文将相位计算等需要大量计算并且可以并行计算的部分移植到GPU上进行计算，利用GPU并发执行的优点，在保证算法精度的同时提高了计算速度。从上述算法的实现可以看出，由于受数据相关性以及编程的复杂性的制约，其只能够对循环结构进行并行化，对分支结构执行效率低下;其次，数据在主存和显存之间的传输也是影响整体速度的主要因素。因此，应在对分支结构的执行和数据的传输这两方面进一步优化。

［1］Zhang Song.Recent Progresses on Real-time 3D Shape Measurement Using Digital Fringe Projection Techniques［J］.Optics and Lasers in Engineering，2010，48（2）:149-158.

［2］谭优.基于FTP的动物体三维面形测量系统的研究［D］.成都:西南交通大学光学工程，2007.

［3］毛先福，陈文静，苏显渝，等.傅里叶变换轮廓术中新的相位及高度算法分析［J］.光学学报，2007，27（2）:225-229.

［4］张彤，刘钊，欧阳宁.基于GPU的图像快速傅里叶变换研究［J］.微计算机信息，2009，25（5）:286-288.

［5］张舒，褚艳丽.GPU高性能运算之CUDA［M］.北京:中国水利水电出版社，2009.3-20.

［6］NVIDIA.CUDAProgrammingGuideVersion2.0［EB/OL］.［2011-9-14］.http://www.docin .com/p-34710013.html.

［7］张启灿.基于傅里叶变换轮廓术的动态物体三维面形测量的研究［D］.成都:四川大学光学，2001.

［8］ Mitsuo Takeda，Hideki Ina* ，SeijiKobayashi.Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry［J］.Opt.Soc.Am，1982，72（1）:156-160.

［9］赵焕东.相位测量轮廓术的理论研究及应用［D］.杭州:浙江大学电子科学与技术，2001.

［10］颜瑞.基于CUDA的立体匹配及去隔行算法［D］.杭州:浙江大学信息与电子工程学系，2010.

［11］田力.CUDA在高性能计算中的应用［D］.杭州:浙江大学理学院，2008.

［12］杜歆，颜瑞.监控摄像机视频去隔行和CUDA加速［J］.传感技术学报，2010，23（3）:393-398.

［13］覃方涛，方斌.CUDA并行技术与数字图像几何变换［J］.计算机系统应用，2009，19（10）:169-172.

［14］SongZhang，Dale Royer，Shing_TungYan.GPU_assisted highresolution，real_time 3D Shape measurement［J］.Optical Society of America，2006，14（20）:9120-9129.

［15］Bi Wenyuan，Chen Zhiqiang.Real-Time Visualize the 3D Reconstruction Procedure Using CUDA［J］.CT Theory and Applications，2010，19（2）:1-8.