辊弯成型力能参数研究

杨世军

（北方工业大学机电工程学院，北京 100144）

成型力矩和成型力是辊弯成型力能参数中十分重要的两个参数。但是由于辊弯成型过程的复杂性，国内外对辊弯成型力能参数的系统研究都很少，得出的一些计算公式也都有很大局限性。文献［1-5］分别从不同方面对力能参数进行了研究，本文主要是从辊弯成型过程中的能量入手来解析成型力矩和成型力，并做出分析。

1 辊弯成型过程中总功和总功率

由文献［6］知辊弯成型变形能由两部分组成即翼缘区和圆角区变形能组成，其变形能的泛函表达式为:

弯曲角的表达式即:

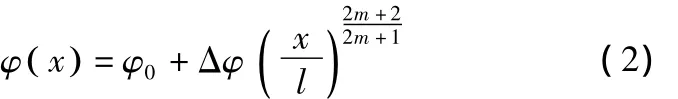
式中，l为变形区长度，其计算公式为:

把式（2）和式（3）两项参数代入到式（1）中解析可得辊弯成型过程总功为:

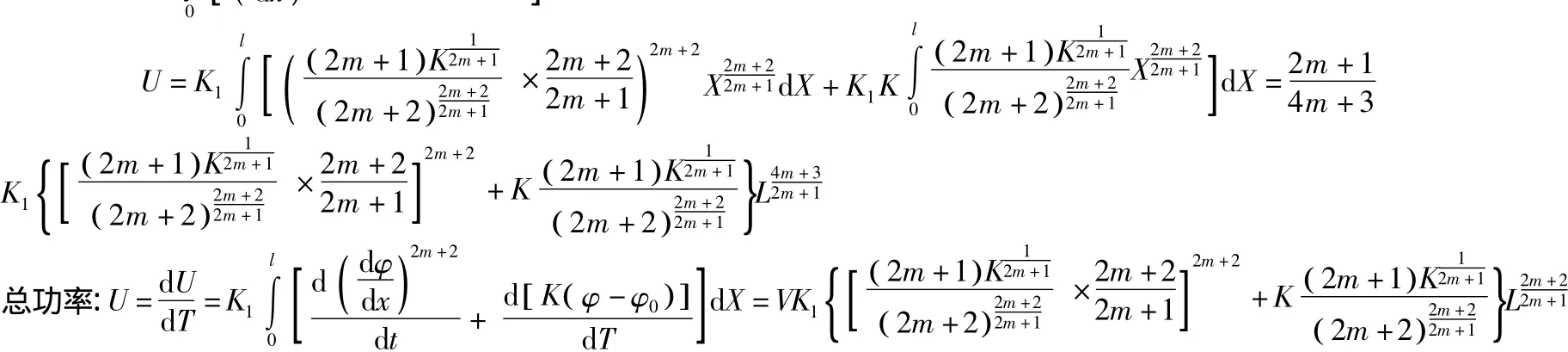
2 成型力矩和成型力计算

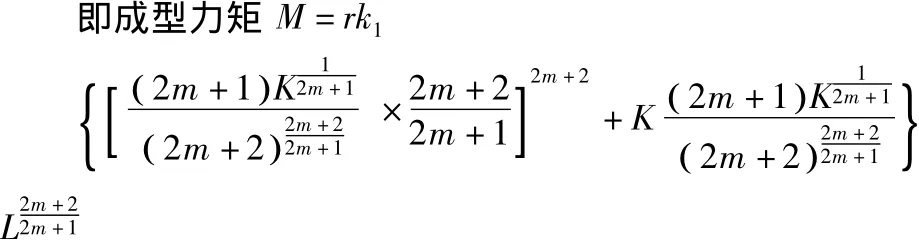
其中:v为板材速度，r为轧辊半径，ω为轧辊角速度。

而在研究成型力时是根据能量即外力做功等于内力功来计算的。

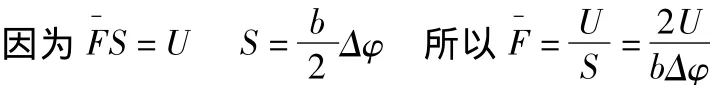
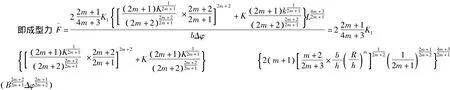
此即为得出的成型力数学计算模型。

3 成型力矩、成型力影响因素分析

为了分析影响辊弯成型力矩的各个要素，在研究时采取其他因素不变，取定值，只对要考察的那个因素取变量来分析。取材料为Q235钢，弯曲半径R=5 mm，材料应变强化指数m=0.1，翼缘腿高b=25 mm，板厚取1 mm，弯曲角增量Δφ=pi/12弧度，轧辊半径R=75 mm，材料应变强化系数根据Q235钢的应力应变曲线插值得B=360;如图1所示。

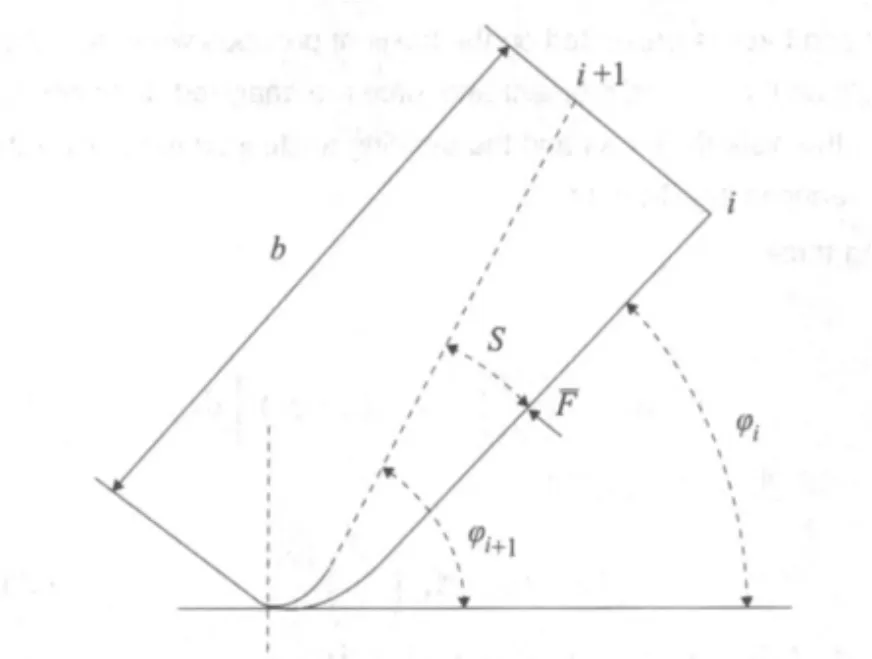
图1 成型力臂S

3.1 板厚h对成型力矩和成型力的影响

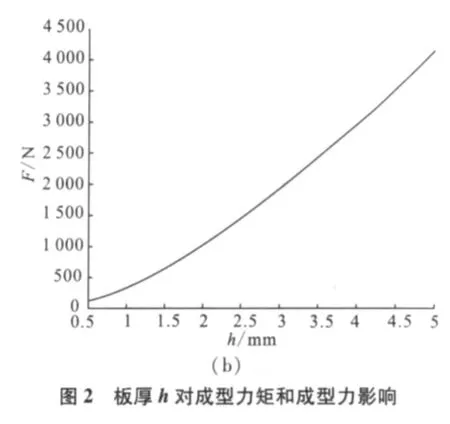
在其他参数不变，取值如上所述，只对板厚h取变化时得对成型力矩和成型力影响如图2。

从图2（a）中可看出随着h值的增大成型力矩M也成指数形式增大;

从图2（b）中可知当材料厚度h从0.5 mm开始增大时成型力F的值随着显著增大。

3.2 弯曲半径R对成型力矩和成型力的影响

在其他参数不变，取值如上所述，只对弯曲半径R取变化时得对成型力矩和成型力影响如图3。

从3图（a）中可看出随着R的增大成型力矩M的值以指数形式下降;

从3图（b）知当弯曲半径R从1.5 mm开始变化时，成型力F随着R值的增大而显著减小，F与R成反比。

3.3 弯曲角对成型力矩和成型力的影响

在其他参数不变，取值如上所述，只对弯曲角取变化时得对成型力矩和成型力影响（图4）。

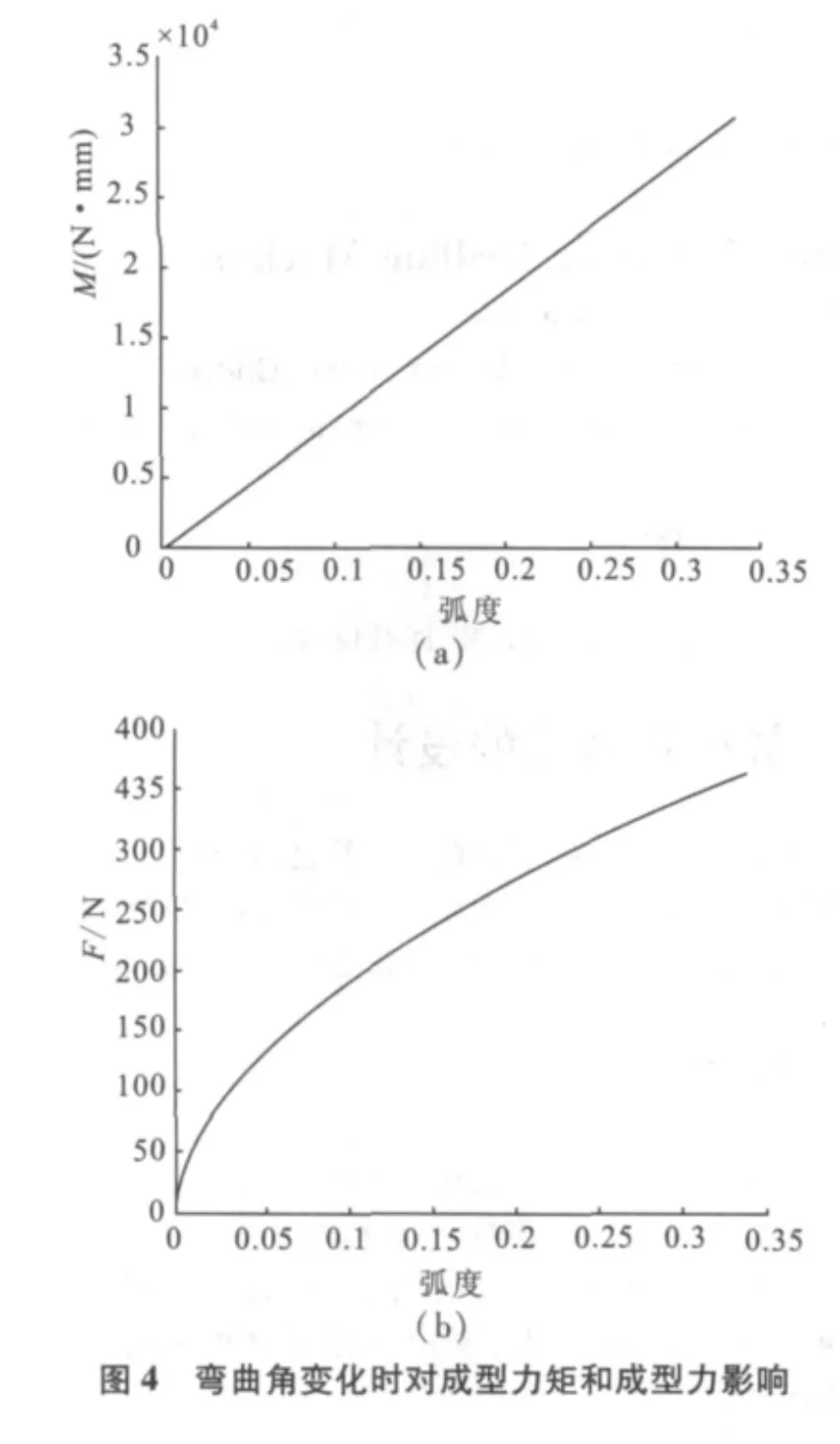
从4图（a）中可看出随着弯曲角的增大成型力矩M的值成线性增大;

从4图（b）知当弯曲角增大时，成型力F增大。

3 结论

通过对辊弯成型过程变形能的研究，根据内外力做功相等原则，推导出了辊弯成型力矩和成型力的数学计算表达式;分析了板厚，弯曲半径和翼缘腿高三因素对成型力矩和成型力的影响。

［1］丁国良.冷弯型钢中力能参数的理论推导［C］.2005中国国际冷弯型钢研讨会论文集，2005，1-10.

［2］兑关锁.冷弯型钢纵向变形的理论分析及计算［J］.钢铁研究学报，1997（02）.

［3］Sukmoo Hong，Seugyoon Lee，Naksoon Kim.A parametric study on forming length in roll forming［J］.Materials Processing Technology，200l（113）:774-778.

［4］S D Zhu，S M Panton，J L Duncan.The effects of geometric variables in roll forming a channel section［J］.Journal of Engineering Manufacture ，1996（210）:27-134.

［5］习荣堂，李景方，樊永义.冷弯成型力研究［J］.东北大学学报，1996，17（1）:94-97.

［6］Γ.Я.古恩.金属压力加工理论基础［M］.北京:冶金工业出版社，1989.8-13.