基于小波神经网络的电动机转子故障诊断
荣明星
(黑龙江科技学院电气与信息工程学院,黑龙江哈尔滨 150027)
0 引言
随着现代工业化进程的发展,电动机已成为了现代工业的主要动力设备,如果电动机因故障而停运将会对生产以至人身安全造成严重的影响。因此有必要建立一套成熟的故障诊断系统。电动机的振动信号最能全面的反应电动机的运行状态[1-2]。由于电动机振动信号是非平稳随机信号[3-4],往往含有大量时变短时突发性质的成分,传统的信号分析方法已不能有效地提取电动机的故障特征,还可能将含有故障信息的微弱信号作为噪声去除。所以采用小波包变换将非平稳信号的各频率成分区分开,小波包变换具有优良的时频局部特性和多分辨率处理能力,能准确的捕捉到非平稳局部突变信号中的故障特征。神经网络所具备的自适应,非线性映射能力等优点[5],使它在故障诊断领域有很大的应用空间,因此可以用神经网络模型来进行故障分类识别。
1 电动机故障诊断方法
电动机故障诊断一般分为信号检测、特征提取、状态识别、诊断决策4个步骤。而使用传感器从被诊断的设备中获得原始信息是诊断的第一步,根据实验条件设计适当的电动机故障诊断方案。本文研究电动机转子在正常,转子不对中,轴承碰磨状态下对应的电动机振动信号,提取有价值的实验数据。以这些数据作为神经网络的输入,建立适合的BP神经网络并在MATLAB上进行仿真,从而研究小波变换和神经网络在电动机故障诊断领域中的有效结合及其应用前景。
2 小波包分析与故障特征提取
2.1 小波变换基本分析[6]
小波是一种持续时间很短的波,其必须满足一定容许条件。同傅里叶分析不同,小波分析的基不是唯一存在的,所有满足小波基条件的函数都可以作为小波函数,所以要依据小波容许性条件确定基本小波。
设ψ(t)∈L2(R),其傅里叶变换为ψ(ω),如果满足:
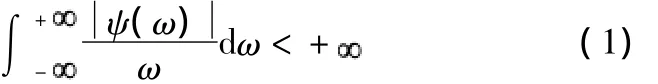
则称ψ(t)为母小波或基本小波。将ψ(t)进行某种伸缩和平移,就得到:
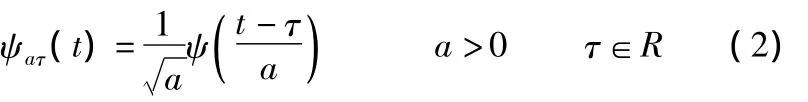
式中:ψaτ(t)为连续小波基函数;a为尺度因子;τ为位移因子。
然后,给定函数f(t)小波变换为:
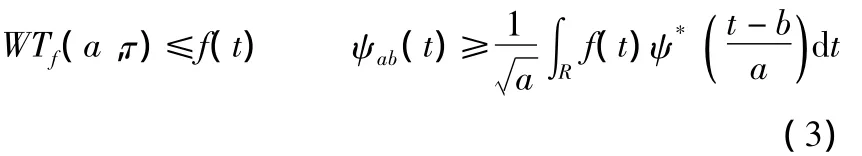
实际运用中,信号要经过计算机分析、处理,必须将信号f(t)变为离散时间序列。对连续小波变换而言,含有的尺度因子和平移因子是连续的,也必须离散,就有了离散小波变换DWT。将尺度因子进行幂级数离散化,令a=,a0>0,j∈Z,位移因子离散化,即,其中,ao和τ0为大于零的实常数,j和k为整数,则得离散小波基函数为:
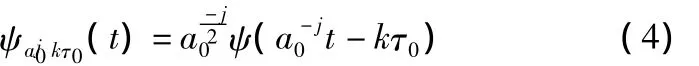
通常取常数a0=2,τ0=1,所以小波基函数简化为
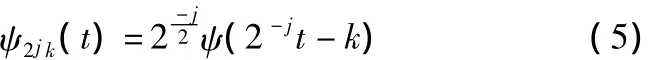
给定函数f(t)离散小波变换可以表示为:
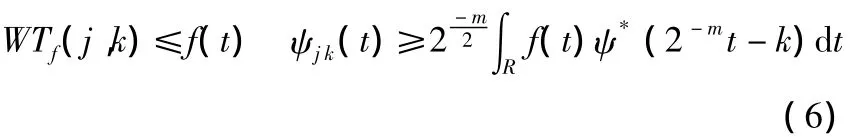
2.2 小波包提取故障特征信号
小波包分析不仅能对尺度空间即低频部分进行分解,还能对小波空间即高频部分进行分解,有很大的优越性,所以得到了广泛运用。小波包分解可以将原信号分解为在不同频带上的投影,对这些频带内的信号进行分析称之为频带分析技术[7]。小波包分析能够将频带进行多层次划分并能根据被分析信号的特征,自适应的选择相应的频带,使之与信号频谱相匹配,从而提高时频分辨率,使故障特征提取能在更加细化的频带内进行。图1以3层小波包分解说明小波包分解过程。

图1 三层小波包分解原理图
图1中(0,0)代表原始信号S,(1,0)代表小波包分解的第一层低频系数,(1,1)代表小波包分解的第一层高频系数,(3,0)代表第0个节点系数,其他均类推。
利用小波包对信号进行重构可以根据需要把干扰和噪声频段清零进行信号重构。因而只要分解时将信号中的特征信号和噪声分解到不同频段上,就可以得到去除干扰噪声的重构特征信号[8]。下面给出小波包特征向量的构造过程[9]:
1)任给信号f(t)∈L2(R)的小波包系数可通过式(3)得到



4)由于小波变换后的ejn得总能量较大,不利于模式分类,对ejn进行如下运算:

构造特征向量,当 j=3 时,T=[E30,E31,E32,E33,E34,E35,E36,E37]在仿真分析中,给出了故障特征提取的具体数据,作为神经网络的训练数据和测试数据。
3 神经网络与故障识别
3.1 BP 神经网络
神经网络是在现代神经学研究成果的基础上提出的模拟人脑某些特性由大量人工神经元组成的并行分布式网络,具有存储经验知识和使之可用的特性。基于BP算法的神经网络是目前应用最广泛的模型属于前馈型网络,又称误差反传算法网络,包括输入层、隐含层和输出层。它的学习规则是通过反向传播来调整网络的权值和阀值使网络误差的平方和最小。包括正向传播与反向传播,在正向传播中学习样本送入输入层,经隐含层运算后传至输出层,如果在输出层没有得到期望结果,则计算输出层的误差变化值,然后进入误差反向传播阶段,误差信号沿着原来的连接从输出层返回输入层并逐层调整连接权值,使误差达到最小。
以电动机为诊断对象,而故障原因和状态之间没有明确的线性关系,不利于用精确的数学模型来描述,可以将电动机的故障状态数据作为样本特征向量输入到神经网络而且给定期望输出。神经网络通过修改神经元连接权值进行训练学习,达到允许的误差范围后停止训练,就可以将其他故障特征向量输入到训练好的神经网络,从而实现故障的识别。
3.2 BP神经网络设计
利用BP神经网络设计一个故障识别器,识别电动机的运行状态。第一步,以小波包分解提取的电动机状态信号的特征向量作为输入样本,如下:
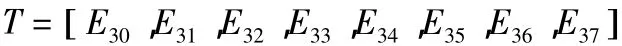
给定相应的期望输出为Xid,用两个输出神经元结点,神经元输出(0,1)表示转子正常,(1,0)表示转子不对中,(1,1)表示轴承碰磨;第二步,根据Kolmogorov定理确定用三层网络结构,输入层,隐含层和输出层的神经元结点数分别为N,2N+1和M,其中N=8,M=2。中间层神经元选择S型正切函数为激活函数,输出层神经元选择S型对数函数为激活函数;第三步,编写BP神经网络程序进行训练,直至训练结果能够满足要求,选择新的测试样本作为训练完毕的神经网络的输入,测试网络性能。过程流程如图2 所示[10]。

图2 BP神经网络算法框图
4 Matlab软件仿真实现
用加速度传感器采集电动机原始振动信号,得到6组样本信号数据,如图3所示。
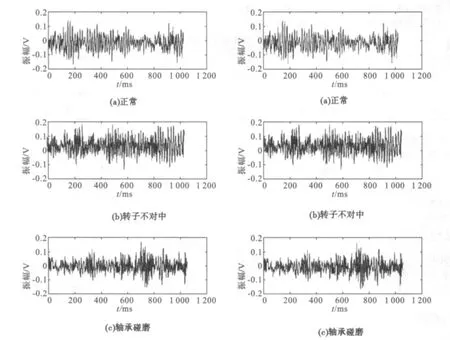
图3 样本信号
将上述信号经过A/D转换和离散化处理后,按特征信号提取步骤利用Matlab编写小波包信号分析程序,对上述样本信号进行特征提取,得到6组样本信号特征向量,如表1。

表1 样本信号特征向量
按照BP神经网络设计步骤,利用Matlab编写BP网络程序,输入样本信号特征向量和期望输出训练神经网络,训练完毕后期望输出和实际输出如表2。
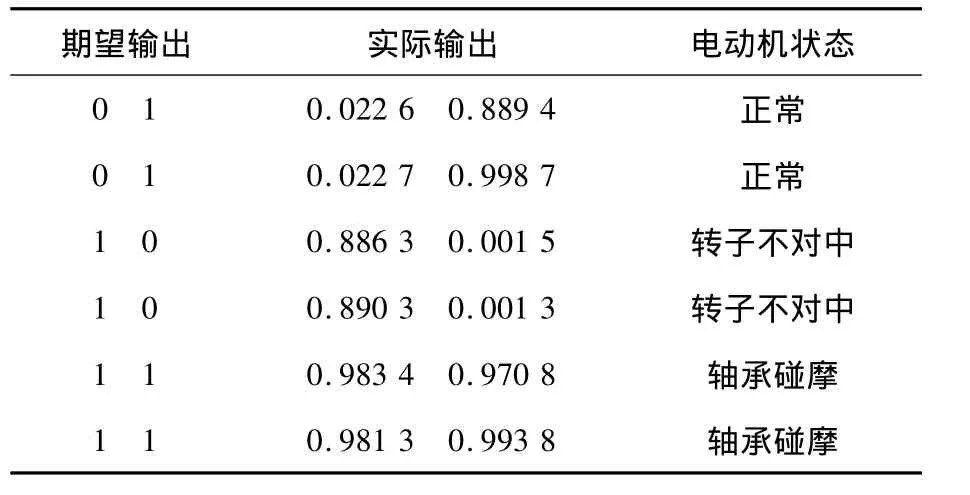
表2 期望输出和实际输出
在误差允许范围内期望输出和实际输出基本一致,表明该网络组成的故障状态识别器训练成功。再同样利用加速度传感器采集另外3组测试信号,经过A/D转换和离散化后的测试信号如图4所示,用于测试训练完毕的神经网络性能。
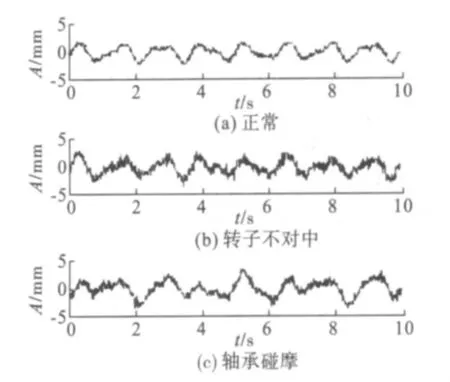
图4 测试信号
利用小波包对测试信号进行分析,提取的特征向量如表3所示。

表3 测试信号特征向量
将测试的3组向量输入到神经网络进行故障状态识别,测试结果如表4所示。

表4 测试输出
测试结果符合信号对应的状态,证明了利用小波包分析能够有效的提取故障特征向量,并用经过训练的BP神经网络能够对电机故障状态做出准确的诊断。
6 结语
本文将小波包分析和BP神经网络结合起来用于电动机的故障诊断。该方法可以有效的用于电动机的故障诊断,利用小波包分析故障信号,克服了傅里叶变换分析信号对故障信号中的微弱和奇异信号成分难以提取的缺点,进一步用神经网络的训练方法进行故障状态识别,实验结果证明了该方法的准确性和有效性,可以实际应用到电动机的故障诊断系统研究应用中,从而对电动机的维护和维修工作提供及时的信息,节省大量的人力和资金。
[1]彭文季,罗兴铸,郭鹏程.基于第2代小波的水电机组振动信号预处理[J].中国电机工程学报,2007,27(30):25-29.
[2]颜秋容,刘欣,尹建国.基于小波理论的电力变压器振动信号特征研究[J].高电压技术,2007,33(l):4-8.
[3]冯志鹏,李学军,褚福磊.基于平稳小波包分解的水轮机非平稳振动信号希尔伯特谱分析[J].中国电机工程学报,2006,26(12):32-37.
[4]钟秉林,黄仁.机械故障诊断学[M].2版.北京:机械工业出版社,2002.
[5]王仲生.智能故障诊断与容错控制[M].北京:国防工业出版社,2005.
[6]刘明才.小波分析及其应用[M].北京:清华大学出版社,2005.
[7]莫琦,陈立定,冯太合.小波包在旋转机械故障振动信号处理中的应用[J].计算技术与自动化,2005,24(2):14-17.
[8]廖传军,罗晓莉,李学军.小波包在声发射信号特征提取中的应用[J].电子测量与仪器学报,2008,22(4).
[9]钱华明,马吉臣,施丽娟.基于小波神经网络的导航传感器故障诊断[J].电子测量与仪器学报,2007,21(增刊).
[10]王平.基于小波神经网络的电机轴承故障诊断[D].山西:太原理工大学,2005.

