液压振动打桩机的自适应模糊PID控制

伏广臣，汤炳新，彭阳阳

（河海大学机电学院，江苏 常州 213022）

0 引言

液压振动打桩机［1］是一种新型打桩机械。它被广泛应用于城市建设、桥梁、港口等各种基础施工工程。它一般与起重机或桩架配套使用，适用于各类钢板桩和钢管桩的沉拔作业，亦适用于混凝土灌注桩、石灰桩、沙桩等诸多类型的地基处理作业。与传统的打桩机相比，液压振动打桩机具有作业环境广、贯入力强、质量轻、沉桩品质好、振动污染小、使用方便等优点。

控制同步是现代振动机械的发展方向。本文提出将双马达同步控制技术应用于打桩机械中，利用双马达带动两组偏心块转动产生的离心力进行打桩，实现无极调频调矩，进而实现不同环境下的最大工作效率。

液压系统液压油的泄露，液压执行元件的非线性摩擦阻力以及外负载的变化使得一般的控制器难以满足控制要求。针对以上问题，本文提出了模糊PID控制方案，综合传统的PID控制的鲁棒性强、易于实现以及模糊控制不依赖受控对象精确的数学模型，能够根据系统变化动态调整控制量的大小，控制灵活、适应性强等特点，从而实现对两组偏心块的精确控制。

1 双马达电液伺服系统偏心块工作原理［2］

图1 液压振动打桩机偏心块结构图

振动打桩是液压振动打桩机区别于其他打桩机的地方，其核心部件为锤头的两组偏心块，原理如图1所示。双马达分别带动上下两根主动轴旋转，每个主动轴通过齿轮分别带动两根从动轴做反向旋转，每个从动轴上都装有两个质量、偏心力矩相同的偏心块，从而带动偏心块作反向运动，偏心块的离心力在水平方向抵消，在垂直方向叠加，叠加的垂直分力随着周期性的转动形成打击力。调节偏心块的转速可以调节振动频率，调节偏心块的相位差可以调节打击力。

2 双马达电液伺服系统同步控制策略

同步控制一般有两种基本形式，一种为“等同控制”，一种为“主从控制”［3］。针对双马达驱动的电液伺服系统，对两组偏心块输出的速度和相位差进行同步控制，具体有以下几种形式。

第一种控制方式由等同控制方式衍生而来（图2），双马达同时跟踪参考速度并根据相位传感器检测出的相位差对双马达的速度进行微调。在这种控制方式下，双马达能够很好的跟踪速度参考值，但是由于双马达动态性能的差异以及诸多外在因素的影响，使得双马达的相位同步难以得到保障。

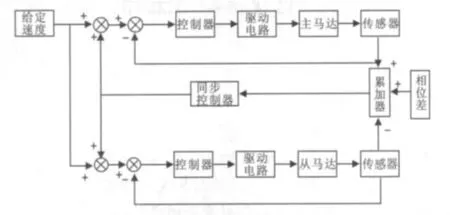
图2 等同式同步控制方框图

第二种控制方式由主从控制方式衍生而来（图3），主动马达跟踪参考速度并根据相位传感器检测出的相位对主动马达的速度进行微调，从动马达以主动马达的输出速度作为参考值并根据相位传感器检测出的相位差对从动马达的跟踪速度进行微调。在这种控制方式下，双马达能够很好的保持相位同步，但对参考速度的跟踪性能会变差。

图3 主从式同步控制方框图

第三种控制方式综合了等同控制以及主从控制的优点（图4），外层采用等同控制方式，双马达同时跟踪参考速度并根据相位传感器检测出的相位差对双马达的速度进行微调，内层采用主从控制方式，主动马达跟踪参考速度并根据相位传感器检测出的相位对主动马达的速度进行微调，从动马达的输入信号由两部分组成，一个为速度参考值，一个为相位传感器检测出的双马达的相位差。在这种控制方式中，双马达既能很好的跟踪速度参考值又能保持很好的相位同步，从而具备良好的同步控制性能，本文采用这种控制方式。

图4 复合式同步控制方框图

3 模糊PID控制［4］

模糊PID控制由模糊化、模糊控制规则、模糊推理和去模糊化四个部分组成（图5）。控制器以偏差e和偏差变化率ec作为输入，根据不同时刻偏差e和偏差变化率ec的值对P（比例）、I（积分）、D（微分）三个参数进行实时调整，从而实现对双马达同步的精确控制。

图5 模糊PID结构图

3.1 模糊量化

一般来说论域的量化等级越高，控制精度越高，对于偏差e和偏差变化率ec，控制量U取其模糊子集的论域为［－6，6］。

偏差e和偏差变化率ec由角位移传感器测得，该传感器传感轴转动范围为0°～360°，输出电压为0～10 V。故可以取偏差的基本论域为［－1r，1r］，偏差变化率的基本论域为［－2r，2r］。

偏差e从基本论域转化到相应的模糊集的论域的量化因子Ke=6，偏差变化率ec从基本论域转化到相应的模糊集的论域的量化因子Kec=12。

模糊变量 E，EC的子集取:“负大”（NB），“负中”（NM），“负小”（NS），“零”（Z），“正小”（PS），“正中”（PM），“正大”（PB）。

隶属函数采用应用广泛的三角形隶属函数。

3.2 模糊控制规则

1）当e较大时，说明误差的绝对值较大，ΔKp取较大值，以提高相应的快速性;为防止ec瞬时值过大，ΔKd应取较小的值;为了避免出现较大的超调，应对积分加以限制，通常取ΔKi=0.

2）当e中等大小时，为了使系统响应超调较小，ΔKp取较小些;在这种情况下，ΔKd对系统响应影响较大，数值要适当;ΔKi的数值也要适当。

3）当e较小时，为了使系统具有很好的稳定性，ΔKp，ΔKi应取较大值，同时为避免系统在设定附近出现震荡，应该考虑抗干扰性能，适当的选取ΔKd的值，ec的取值与ΔKd的取值规律相反，通常情况ΔKd为中等大小。

3.3 模糊推力计算和去模糊化e方法

模糊推理的算法有Takagi-Sugeno-Kang［5］型模糊推理算法、Larsen型模糊推理算法、Mamdani型模糊推理算法等。去模糊化方法主要有最大隶属度法、面积中心法、加权平均法、面积平分法等。与其他模糊推理算法相比，Takagi-Sugeno-Kang型模糊推理算法具有算法简单、易于与PID结合等优点，因此本文采用Takagi-Sugeno-Kang型模糊推理算法，并采用加权平均法进行去模糊化，从而获得不同时刻PID三个参数。

4 实验分析

振动打桩机在实际工作中，外界环境变化以及不同土壤，对其性能会产生很大影响。精确、稳定的性能才能确保打桩机的工作效率。利用Labview［6］，强大的实时性能对PID控制以及模糊PID控制进行对比实验分析，设置转速为100 rad/s，相位差为120°，得到实验结果如图6，图7所示。

从上图可以看出，在相同的外界环境下，模糊PID比PID都能对双马达进行有效地跟踪控制，但是在PID控制方式下，双马达的相位差始终在设定值上下震荡，而在模糊PID控制方式下双马达的相位差始终能够平稳地跟踪设定值，从而使打桩机具有更出色的打桩性能，因此相对于单纯的PID控制，模糊PID控制器同步控制更加精确，控制性能更加优越。

5 结论

结合了同步控制与主从控制的控制方式，使得两个偏心块即使在外界的干扰下，也能保持良好的同步性能。针对电液伺服系统的时变性、非线性以及模型不确定性等特点，提出了基于Takagi-Sugeno-Kang模型的模糊PID同步控制方法，该控制方法具有响应速度快、响应过程平稳、稳态误差小、抗干扰能力强等特点，对复杂控制系统及高精度伺服控制系统具有良好的控制性能。

［1］刘军玉.液压振动打桩机设计［J］.农业装备与车辆工程，2007（12）:32-34.

［2］王玥，赵伟民，付海龙，等.振动打桩机偏心块的参数研究与有限元分析［J］.机械工程师，2005（7）:132-134.

［3］赵春雨，朱洪涛，闻邦椿，等.多机传动机械系统的同步控制［J］.控制理论与应用，1999，16（2）:179-183.

［4］赵艳，王孟效，张根宝，等.Sugeno模糊推理实现PID的分层控制及仿真研究［J］.现代电子技术，2005，28（7）:94-96.

［5］钟飞，钟毓宁.Mamdani与 Sugeno型模糊推理的应用研究［J］.湖北工业大学学报，2005，20（2）:28-30.

［6］羊箭锋，黄平，肖圣兵，等.基于LabVIEW振动主动控制实验仿真研究［J］.实验技术与管理，2011，28（7）:98-101.