某动能防暴弹恒定落点动能弹道解算技术
翟杰,徐万和,仲其伐
(南京理工大学机械工程学院,江苏南京 210094)
0 引言
动能防暴弹在公安战线使用的主要问题是:能否保证有效的执法效能和非致命效果,这一问题严重制约了动能防暴弹在公安战线上的应用。由于目标的距离不同、目标的穿戴不同,形成了非致命动能防暴弹的作用效果与非致命要求的矛盾。初速过高,会使近距离目标和穿戴单薄目标发生致伤、甚至致命的后果。初速过低,对远距离目标和穿戴厚实目标失去作用。本文主要研究在有效射程内,为保证恒定落点动能打击时,目标距离与弹丸射击初速度的匹配关系以及各射角状态下落点速度的波动关系。
1 恒定落点动能与新型变初速防暴武器原理
恒定落点动能是指对于不同距离的目标,动能弹弹丸打击目标的能量始终是一致的,只要能够控制动能弹弹丸的打击能量值,就解决了防暴弹作用效果与非致命要求的矛盾。新型变初速防暴武器基本原理为:首先通过安装在防暴枪上的激光测距装置测量出目标的距离,然后自动调节防暴枪的相关装置,调节防暴动能弹弹丸的发射初速度,不同的射击距离匹配不同的初速度,以达到恒定落点动能的目的,从而达到对不同距离、不同穿戴情况目标的定效能打击[1]。
2 恒定落点动能的选择
动能防暴弹主要依靠飞行弹丸的动能打击目标,使目标失去抵抗能力,同时又不能产生致命伤害。目前,美国和德国等多数国家都以78 J作为对生动目标杀伤的标准,法国定为39 J,我国定为98 J,也有以比动能(弹丸动能与其迎风面积的比值)作为标准的,军用致命弹头或破片的最小比动能为26 J/cm2[2]。本文初步设定,在夏天目标穿戴单薄的情况下,落点动能选择为10 J,在冬天目标穿戴厚实的情况下,落点动能选择为30 J,在春秋季节,落点动能选择为20 J。
3 恒定落点动能弹弹道模型
3.1 弹道模型方程
基本假设:在弹丸整个运动期间,假设章动角(或攻角)δ=0;弹丸是轴对称体;地表为平面;重力加速度的大小不变(g=9.80 m/s2)和方向始终铅直向下;科氏加速度为零。也就是对地球旋转的影响只考虑了包含在重力内的惯性离心力的部分;气象条件是标准的,无风雨;忽略音速的变化,取音速为常量,a=341 m/s。
以距离x为自变量的弹丸质心运动方程组为:
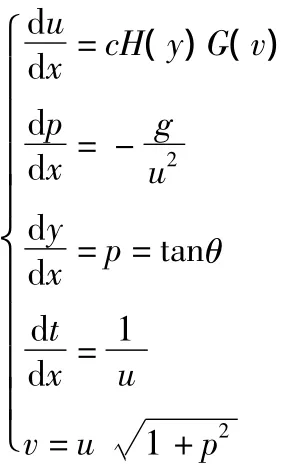
式中:u为弹丸水平分速度,θ为弹道倾角,v为弹丸速度,c为弹道系数,H(y)为空气密度函数,G(v)为空气阻力函数[3]。
3.2 计算结果
借助Matlab软件以四阶龙格库塔编写了弹道程序,并对某18.4 mm动能防暴弹在10 J,20 J,30 J三种落点动能条件下,进行了求解。动能弹弹道系数为35.796,阻力系数为0.259,空气阻力函数为常量0.999,阻力系数为0.259,弹丸击中目标高1.5 m处。得到0~100 m射程内射距与初速的关系如表1所示。

表1 射距与初速的关系
从表1可以看出,随着射击距离的增加,要实现恒定落点动能打击,所需弹丸初速也随之增加,如图1所示。通过连续调节弹丸的发射速度可以实现不同射击距离上的恒定落点动能打击。对于10 J落点动能方案,当射击距离从10 m增加到100 m时,初速从51 m/s增加到81 m/s,速度调节范围为30 m/s;对于20 J落点动能方案,当射击距离从10 m增加到100 m时,初速从71 m/s增加到108 m/s,速度调节范围为37 m/s;对于30 J落点动能方案,当射击距离从10 m增加到100 m时,初速从87 m/s增加到130 m/s,速度调节范围为43 m/s;由此可见变初速防暴武器的速度调节范围至少在45 m/s左右,才能保证0~100 m射程内的恒定落点动能打击。
3.3 速度波动量的分析
因为前面射距与初速的关系是基于水平射击的状态(射角为0°)下计算的,但实际情况中射角一般在-10°到10°之间,所以如果仍然以前面计算得出的初速度进行射击,落点速度肯定存在一定的波动误差,但是弹丸落点速度波动误差是否在合理范围之内,需要进一步进行验证。下面分别对10 J,20 J,30 J在0~100 m射程内进行落点速度波动量分析。
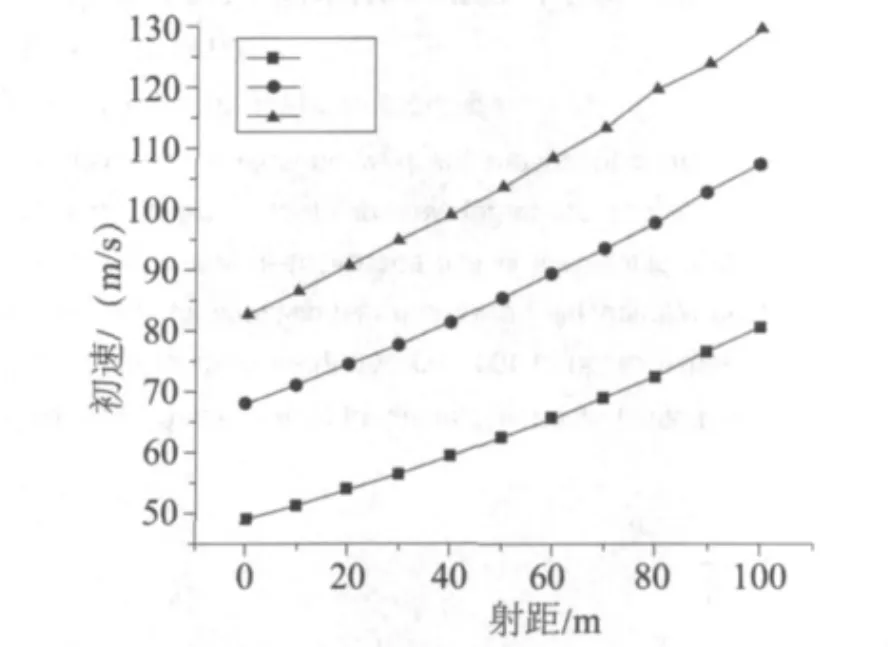
图1 射距与初速的关系
表2表明在射角为10°的情况下,对于E=10 J方案,0~100 m范围内落点速度波动在0.14% ~4.35%范围内;对于E=20 J方案,0~100 m范围内落点速度波动在0.03% ~0.55%范围内;对于 E=30 J方案,0~100 m 范围内落点速度波动在0.02% ~0.67%范围内。
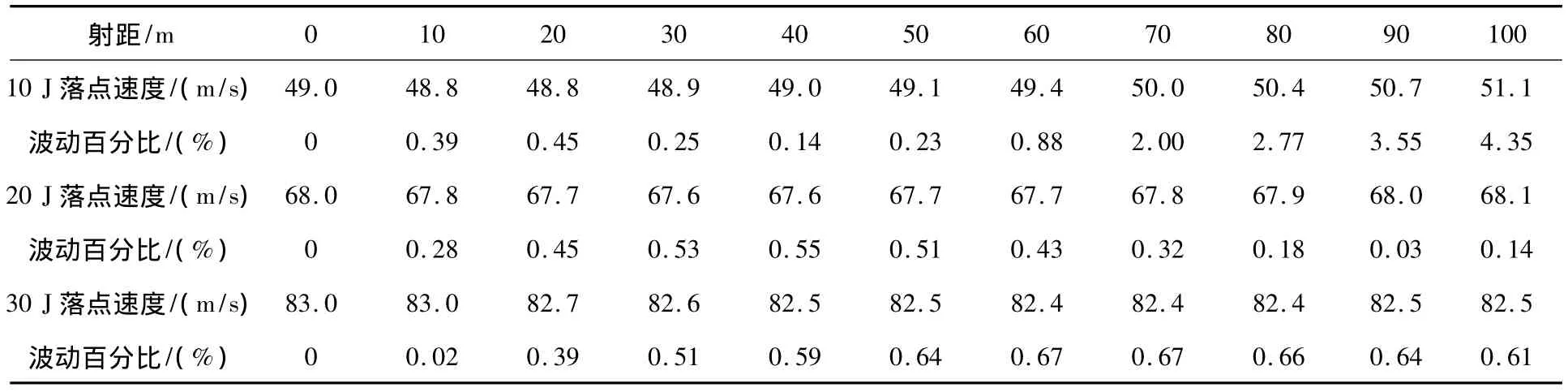
表2 射角为10°落点速度的波动情况
表3表明在射角为5°的情况下,对于E=10 J方案,0~100 m范围内落点速度波动在0.02% ~7.27%范围内;对于E=20 J方案,0~100 m范围内落点速度波动在0.02% ~1.64%范围内;对于E=30 J方案,0~100 m范围内落点速度波动在0.02% ~0.57%范围内。
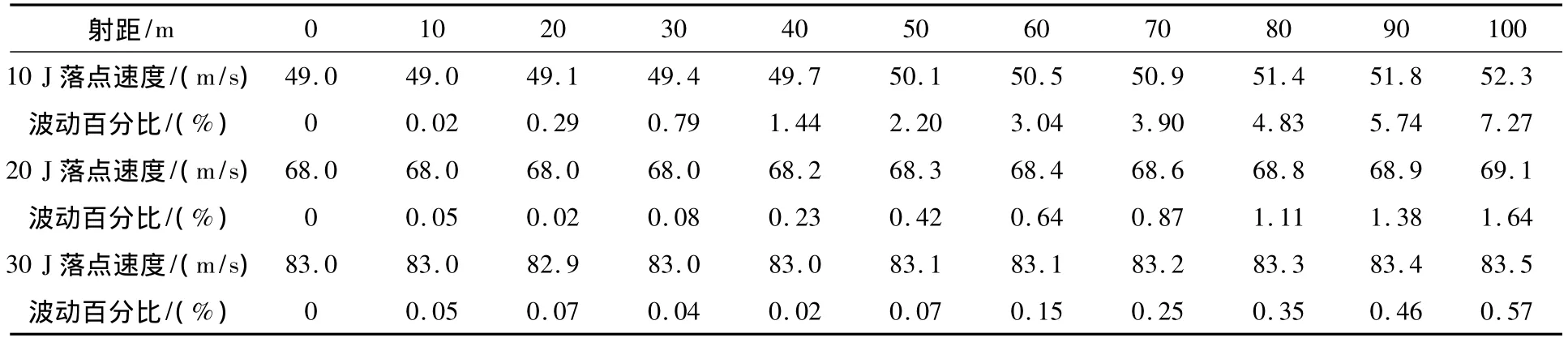
表3 射角为5°落点速度的波动情况
表4表明在射角为-5°的情况下,对于E=10 J方案,0~100 m范围内落点速度波动在0.66% ~10.1%范围内,其中在100 m距离上速度波动超过了10%;对于E=20 J方案,0~100 m范围内落点速度波动在0.29% ~3.58%范围内;对于E=30 J方案,0~100 m范围内点速度波动在0.18% ~1.89%范围内。
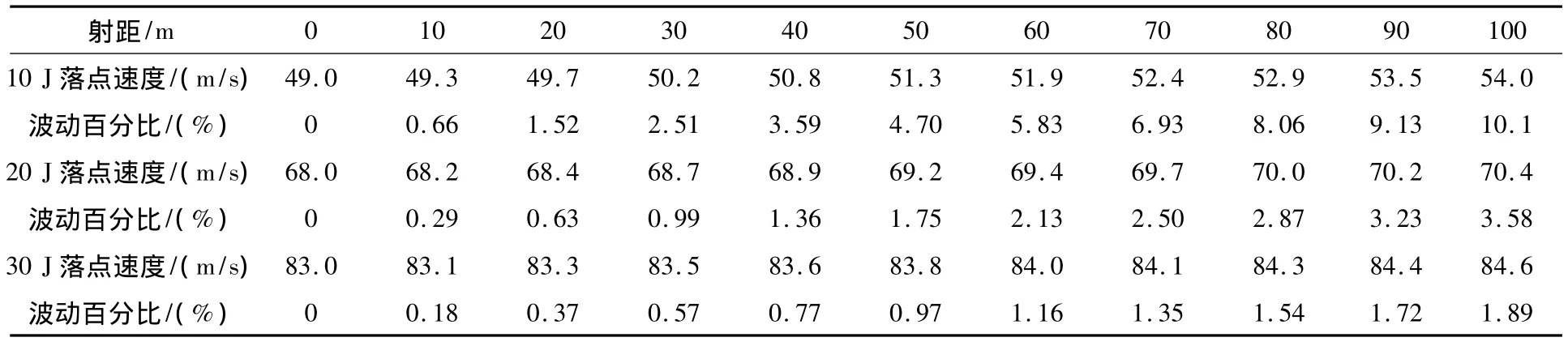
表4 射角为-5°落点速度的波动情况
表5表明在射角为-10°的情况下对于E=10 J方案,0~100 m范围内落点速度波动在0.95% ~11.4%范围内,在90~100 m距离上落点速度波动超过了10%;对于E=20 J方案,0~100 m范围内,落点速度波动在0.42% ~4.04%范围内;对于E=30 J方案,0~100 m范围内,落点速度波动在0.24% ~2.04%范围内。
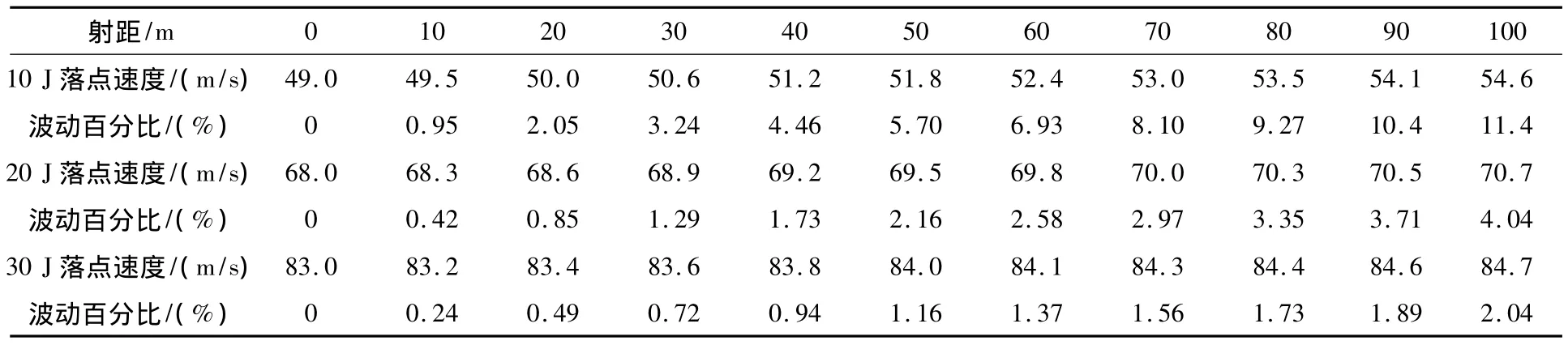
表5 射角为-10°落点速度的波动情况
由图 2、3、4 可以看出在 E=10 J、E=20 J、E=30 J三种方案下,5°,10°的射角状态下,落点速度都是先下降再上升,-5°,-10°的射角状态下,落点速度为持续上升。
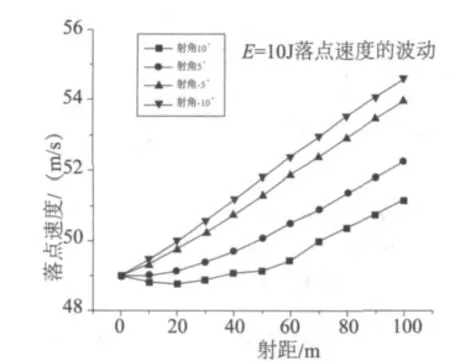
图2 E=10 J落点速度波动
4 结语
通过对某防暴弹恒定落点动能的理论建模和数值计算,表明:
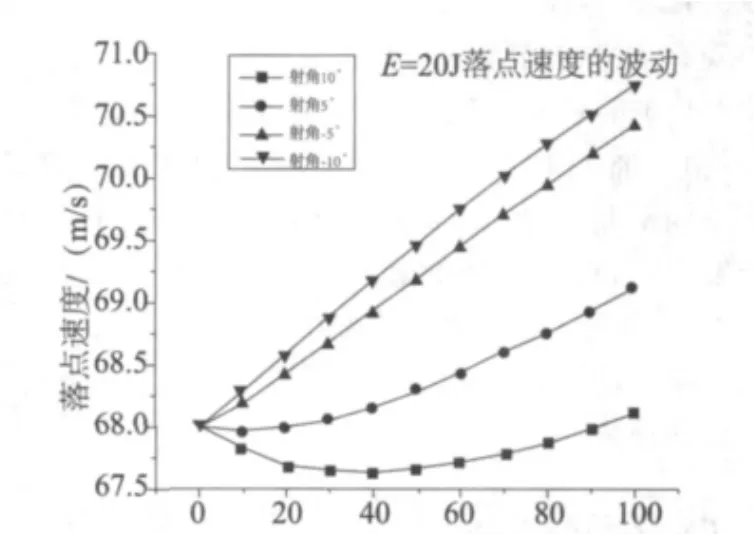
图3 E=20 J落点速度波动
1)通过对初速的连续调节,可以实现不同射击距离上的恒定落点动能打击。
2)在-10°~10°射角范围内,得到了落点速度的波动的规律。
3)通过对18.4 mm防暴动能弹的分析计算,得到了一套完整的恒定落点动能弹道计算方案。
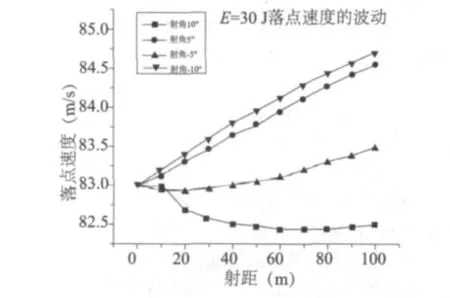
图4 E=30 J落点速度波动
[1]冉景禄,徐诚,牛福强.定效非致命杀伤变初速发射原理[J]南京理工大学学(自然科学版),2010,34(6):765-769.
[2]王文,刘斌胜,赵志亮.防暴动能弹设计原则[J]山西科技,2010,25:103-104.
[3]浦发,芮筱亭.外弹道学[M].北京:国防工业大学出版社,1980.

