一种相控阵雷达数据处理中的杂波抑制方法

熊美英，陈 静

（船舶重工集团公司723所，扬州225001）

0 引 言

现代雷达已采用先进的信号处理技术，运用了很多对杂波抑制的手段，如动目标显示（MTI）、动目标检测（MTD）、恒虚警率（CFAR）等，能够有效地抑制虚警杂波，保持适当的检测能力；但在气象条件恶劣、地势地形复杂的工作环境下，仍然会出现较高的杂波剩余现象［1］。这些剩余杂波增加了数据处理的运算量和存储量，产生的虚假点迹干扰了真实目标的航迹起始，增加了监控区域内航迹相关的复杂度，在相控阵雷达体系中对自动转入跟踪任务的虚假航迹还会占用系统调度资源，干扰作战决策，严重影响对正常目标的探测。因此，在进行常规的数据处理前，预先对回波信号进行一系列的杂波抑制处理，尽可能减少杂波对数据处理的影响，具有重要的实际意义。

1 杂波特性分析

雷达杂波种类复杂繁多，对检测能力影响较大的主要有地杂波和海杂波。地杂波是一种面杂波，它的平均回波功率为：

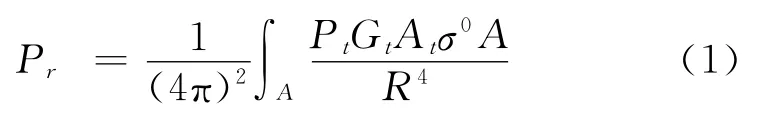
式中：Pr为接收功率；Pt为发射功率；Gt为发射天线增益；At为接收天线面积；R为距离；A为雷达天线的照射区域，σ0为地面散射系数。

发射波束覆盖杂波区面积越大和后向反射系数越大，地杂波越强。地杂波的随机起伏特性可以用概率密度分布函数和功率谱来表示，地杂波的起伏特性符合高斯分布，其高斯概率密度函数为：

式中：μ为x的均值；σ2为x的方差。

地杂波的幅度符合瑞利分布，其瑞利分布的概率密度函数为：

式中：b为瑞利系数，瑞利分布的均值μ和方差σ2分别为：

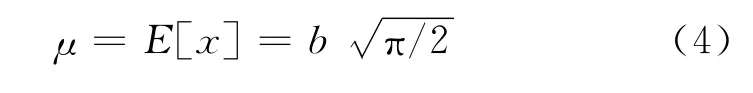
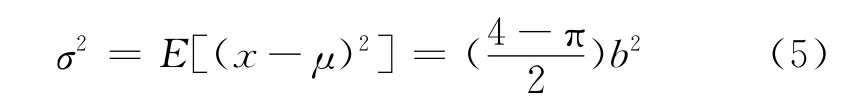
海杂波概率也可以用高斯分布来表示，其幅度概率密度分布也符合瑞利分布，但它受到风速、风向、洋流、水温等海面状态因素的影响而更为复杂，其概率分布时常会偏离高斯分布，有时需要采用更多的非高斯模型来分析，如对数正态分布、韦布尔分布和K分布等模型。

2 数据处理中杂波抑制

尽管在数据处理阶段对杂波的抑制可利用的信息不如信号处理多，实时性不如信号处理强，但是通过对杂波特性的分析、回波信息的积累、比较及综合判断，也可以有效地滤除杂波信号。分析某型相控阵雷达真实发射状态下的信号处理输出回波信息，尝试在数据处理中做了以下改进。

2.1 单波束内杂波滤除

每次收到来自信号处理的搜索波束数据时，对每个距离单元上过门限数据进行第1次杂波滤除。采集数据如表1所示，该数据为一个发射波束指向，方位上固定间隔的相邻四接收波束连续距离单元上，过门限回波信号幅值和跨距离宽度。

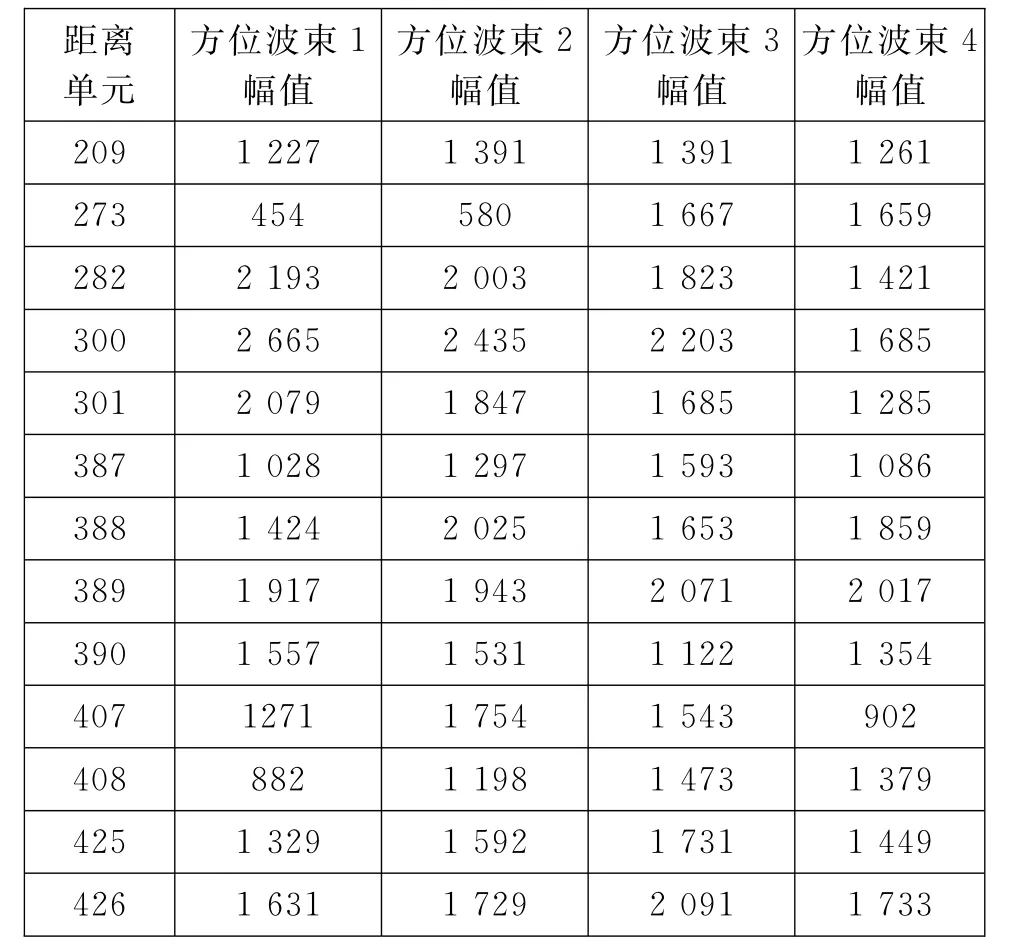
表1 回波信号幅值和跨距离宽度

回波信号幅值反映目标回波的能量，回波跨距离宽度是指回波模拟信号经过采样量化和信号处理幅度检测后占据的连续距离单元个数。分析数据发现杂波和真实目标的回波信号在幅度和跨距离宽度上都有所区别，利用这个特征设置门限，剔除一部分杂波。通过数据统计发现，真实目标回波跨距离宽度一般都占据连续2个距离单元以上，所以可以将回波跨距离宽度设置为2，则表1中209、273、282的距离单元上孤立的回波被当作杂波滤除掉。接下来，对于连续占据2个距离单元的回波加设幅度门限，根据距离远近调整不同幅度门限值，幅度低于门限值的点迹予以剔除。幅度门限值设置的基本依据是雷达方程［2］和平面相控阵天线方向图函数［3］，分别见公式（6）和公式（7）：

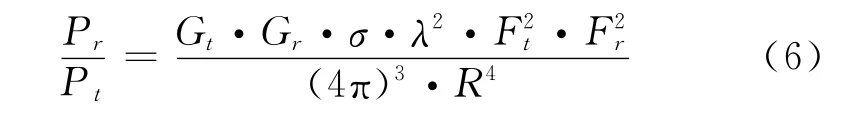
式中：Pr为接收功率；Pt为发射功率；Gt为发射增益；Gr为接收增益；σ为目标RCS；λ为当前发射频率频点折算的波长；Ft为发射方向图；Fr为接收方向图；R为目标距离。

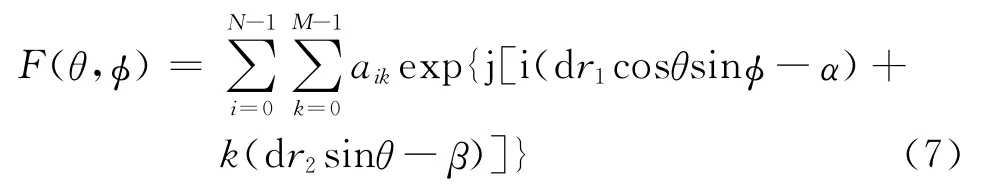
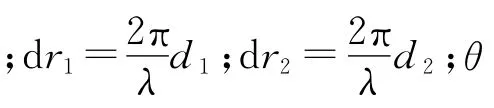
公式（6）、（7）中各项根据雷达的实际参数进行设置，幅度门限值即为接收功率的开平方，依据雷达各项参数设置幅度门限后，表1中距离单元为425、426的回波被排除。由于该方法计算量较大，考虑到数据处理的实时性要求，可以预先装订好雷达参数和关注目标特性，将幅度门限按照距离制成表格文件直接调用。

此外，数据处理中还可以针对每个回波的MTD通道号来进行杂波抑制，可以将径向速度在零附近的回波数据剔除。

2.2 全扫描区域杂波图门限比较

对于已经进行过单波束杂波滤除的数据，再进行一次全扫描区域的杂波图门限比较，只有高于门限的回波才会进行数据处理。全扫描区域杂波图是扫描范围内按方位－距离单元分布的回波强度图。方位－距离单元的划分方法［4］如图1所示，阴影部分为1个方位－距离单元。

1个方位－距离单元包括多个接收波束的连续几个距离单元，将其中的回波幅度信息进行平均，得到幅度均值，每次扫描后得到的均值通过公式（3）进行迭代，即可获得杂波图中方位－距离单元上的杂波均值［4］：

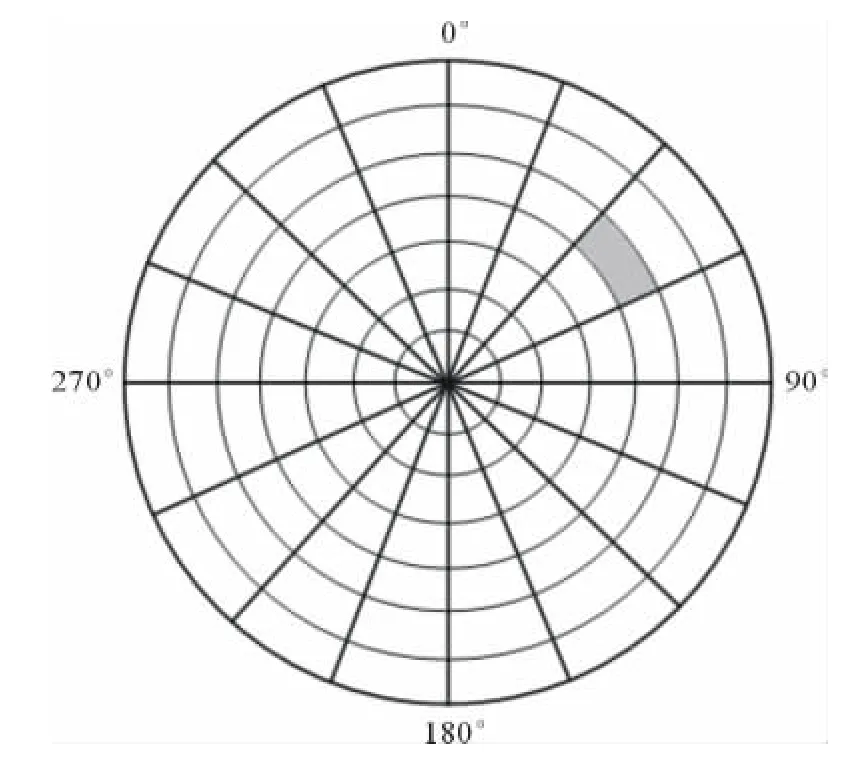
图1 方位－距离单元的划分方法

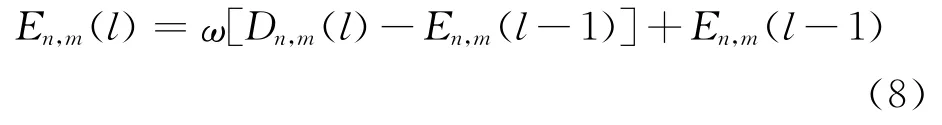
式中：n、m分别为方位、距离单元索引；l为天线扫描周期数；ω为滤波系数，一般取经验值0.125。

由于杂波影响最严重的一般为低仰角，所以全扫描区域杂波图采用了低仰角的扫描层数据进行更新，对杂波干扰严重的低仰角数据才进行杂波图门限比对。对于快速目标（如飞机、导弹等），从一次扫描到下一次扫描一般移动几个距离单元，所以杂波图对运动目标影响不大。

2.3 杂波图的空间重定位

空间杂波图方位－距离单元的划分建立在绝对坐标系的划分方法上，所以需要分析雷达载体处于运动状态时对建立的杂波图的影响和解决办法。在平台运动方向的坐标系中，杂波图的空间重定位可以通过公式（9）、（10）进行计算：

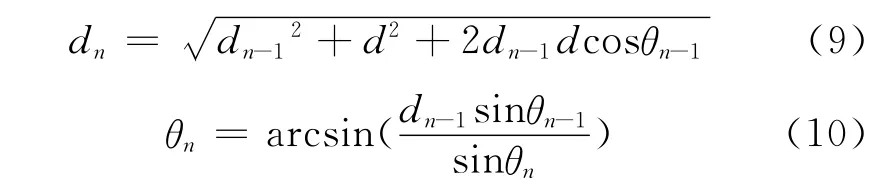
式中：d为雷达载体从周期Tn－1到Tn之间的运动距离；dn－1、θn－1分别为杂波图中的任意一个方位－距离单元在Tn－1时刻的距离、方位；dn、θn分别为该方位－距离单元在Tn时刻的距离、方位。

当雷达载体位置发生变化时，对杂波图中的每个方位－距离单元进行上述的空间重定位的计算量是非常大，工程应用中难以实现。因此，需要针对公式进行进一步简化处理。首先，d远小于dn－1、dn，可以将式（9）简化为：

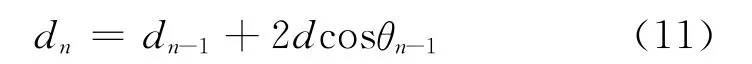
此外，在杂波图的建立过程中，迭代周期内方位－距离单元还没有形成一个比较可靠的阀值，可以粗略地在距离向做归一化处理。通过事先做好方位－距离变化的对应表格，在实际工作中直接查表计算由于雷达载体运动造成的空间重定位，减少了复杂三角运算的计算量，能更准确实时地更新杂波图数据。

3 杂波抑制效果比对

选取1组真实发射数据，搜索区域为法线方向（－30°，30°），扫描周期为1s，累计100个周期，统计结果如表2所示，显示效果如图2、图3所示。

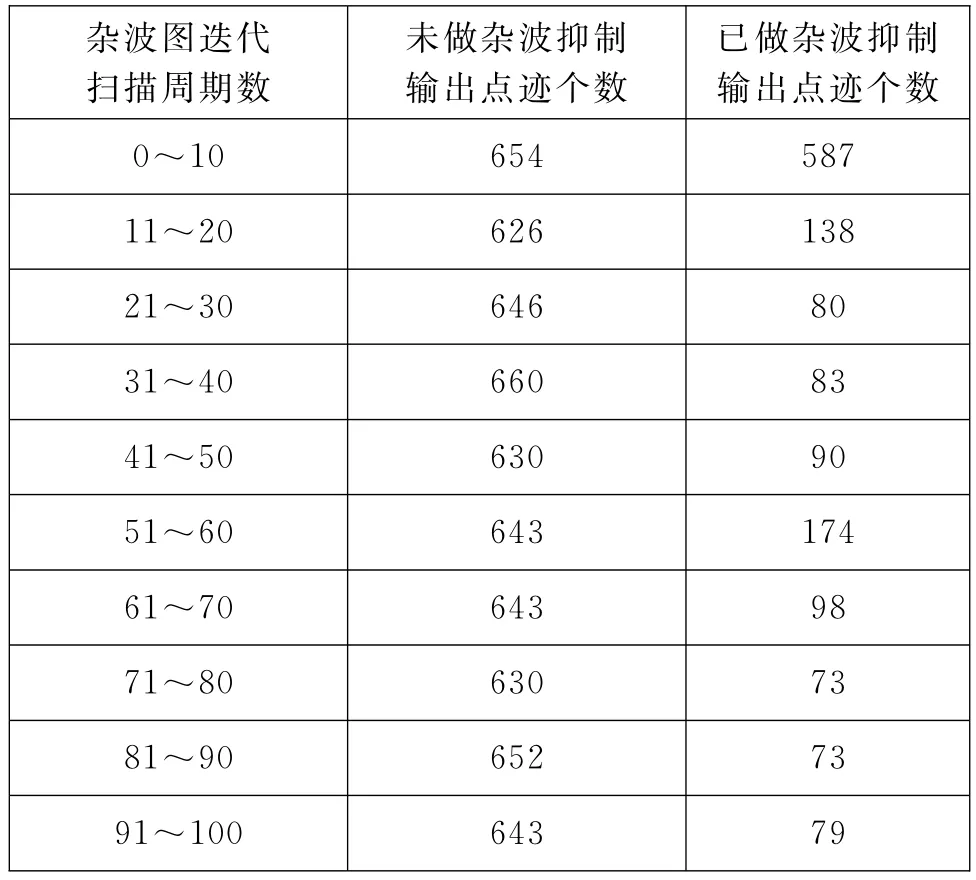
表2 杂波图迭代数据

图2为未做杂波抑制处理的数据处理结果显示，每10个周期累计点迹数在600以上，100个扫描周期内虚警航迹数15条，受杂波点影响，真实目标航迹无法起始，而且由于单个波束点迹处理能力饱和，造成距离较远的回波无法得到处理。

图3为已做杂波抑制处理的数据处理结果显示，刚开始10个周期内的累计点迹数在500以上，经过杂波抑制后，10个周期内的点迹累计数基本降到100以内，并且在100个扫描周期内，虚警航迹0条，真实航迹1条，该目标航速在60m／s，表明运用杂波抑制处理后，较慢速的真实目标回波并没有被抑制掉，因此该抑制方法对运动目标的影响不大。此外由于杂波抑制后，单波束的点迹处理负担减弱，远距离的回波也能被处理为点迹输出，保证了设备发现目标的能力范围。

图2 未做杂波抑制数据处理结果显示

经过比对，上述方法对杂波抑制效果比较明显。杂波抑制在数据处理阶段的运用比较灵活，可以针对某个区域，可以选择做哪种抑制处理，可以选择抑制参数大小，这些都可以随着现场杂波环境和设备关注目标类型进行选择和调整，有效防止了真实目标丢失现象。

4 结束语

本文介绍了相控阵雷达数据处理中一种杂波抑制的方法，通过试验数据效果比对，该方法对杂波的抑制作用明显，但仍然存在杂波剩余，需要进一步对杂波特性进行分析，使得雷达性能获得更好的改善。

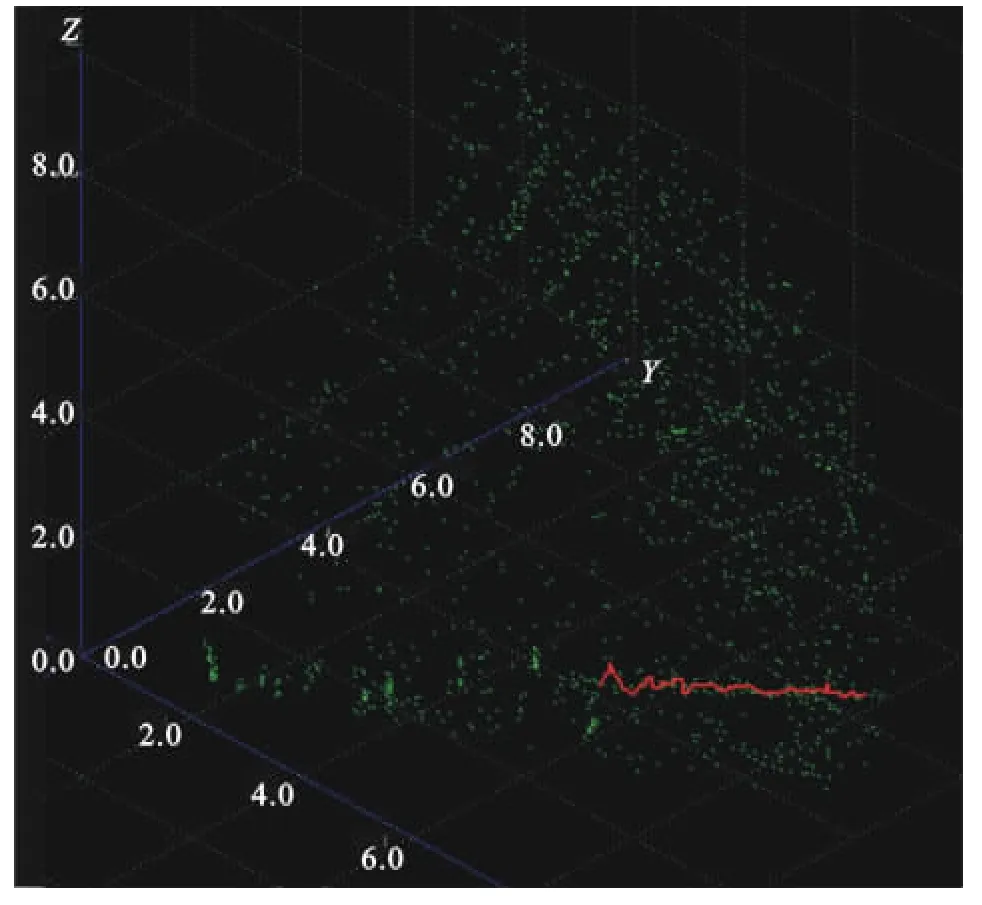
图3 已做杂波抑制数据处理结果显示

［1］何友.雷达数据处理及应用［M］.北京：电子工业出版社，2009.

［2］［美］斯科尼克.雷达手册［M］.王军译.北京：电子工业出版社，2003.

［3］张光义.相控阵雷达技术［M］.北京：电子工业出版社，2006.

［4］吴顺君.雷达信号处理和数据处理技术［M］.北京：电子工业出版社，2008.