一种构造任意4k阶保块和完美幻方的简便方法

王正元

（中国石油天然气股份有限公司，北京 100007）

在一个4k阶幻方A=（aij）4k×4k中，若任意2×2连续方阵（简称二阶方块）中的4个元素之和均相等，则称幻方A为一个保二阶块和幻方，简称保块和幻方.文献[1]和[2]给出了构造任意4k阶保块和完美幻方的两组公式，但其不足之处是公式显得较为繁复，且对任一指定的4k阶，一组公式仅能构造出一个幻方.本文将给出一种简便的方法，既无需繁杂的计算，又能构造出一大批保块和完美幻方.

1 构造方法

首先，将0～（4k-1）的数按（0，4k-1），（1，4k-2），（2，4k-3）……的方式两两配对，共分为2k组，每组两数之和均为4k-1.然后，从其中任取k组，将这2k个数按任意顺序填入4k阶方阵的第一行奇数列的方格中；再将剩下的k组2k个数以任意顺序填入方阵第一行偶数列的方格中.然后，在每一列中，用所填数的互补数（即其所在数对中的另一数）与该数交替填满该列，得到方阵B.令

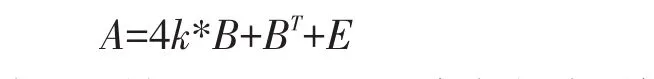
其中BT为方阵B的转置，E为4k阶单位方阵（其中每一个元素均为1），则A为4k阶保块和完美幻方，其中任意二阶方块中4个元素之和均为幻和的1/k.

以8阶为例说明一下构造的过程.首先，将0～7的数分为4组：（0，7），（1，6），（2，5），（3，4）.从中任取2组，如（0，7），（3，4），将其中4个数以任意顺序填入8阶方阵第一行的奇数列，将剩余2组的4个数（1，6，2，5），以任意顺序填入方阵第一行的偶数列（见图1）.

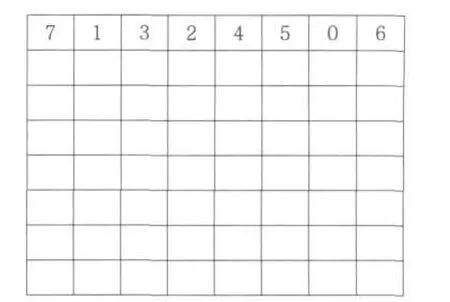
图1 B方阵首行Fig.1 The first line of square B

下一步，将已填数的互补数填入各列，使两数交替填满该列，得到方阵B（见图2）.

计算A=8k*B+BT+E，得8阶方阵A（见图3）.

可以验证方阵A为完美幻方，且是保块和的，其任意二阶方块中4个元素之和均为130，恰为8阶幻方幻和260的1/2.

图2 方阵BFig.2 Square B

图3 8阶保块和完美幻方Fig.3 8-order conserve square sum perfect magic square

2 方法的证明

首先证明，方阵B为一广义完全拉丁方，即其行、列及各泛对角线各元素之和均相等.

B方阵的行列和相等是显然的，因其各行之数均历遍0～（4k-1），和为2k（4k-1）；每列由1个数对中的两个数填满，共重复2k次，而每个数对2数之和为4k-1，故其和亦为2k（4k-1）.

下面证明方阵B的任一对角线（包括泛对角线）各数之和也等于2k（4k-1）.先考察主对角线（从方阵左上角至右下角的对角线）.记B=（bij）4k×4k，并记第一行各数分别为 a1，a2，a3，…，a4k；a1～a4k历遍0～（4k-1）.根据构造法，易知：

其中j=1，2，…，2k.因此，主对角线各数之和为

再由构造法易知，在与主对角线平行的4k-1条泛对角线中，其中2k-1条上的各列之数与主对角线上该列之数对应相同，因而和也为2k（4k-1）；而另2k条上各列之数为主对角线该列之数的互补数，则其和为：

对副对角线（从方阵左下角至右上角的对角线）及其平行的泛对角线进行同样的分析，也可得其和为2k（4k-1）.故B的行、列、泛对角线各数之和均相等，B为一广义完全拉丁方.

下面证明 B 与 BT正交.若存在（bij，bji）=（bi’j’，bj’i’），按数偶相等的定义，有

若 aj≠aj'，应有 aj=4k-1-aj'，于是 aj+aj'=4k-1.这说明aj与aj'是互补数对中的两数，而根据构造法，必有j与j'奇偶性相同.

然而，若j与j'同为奇数，有

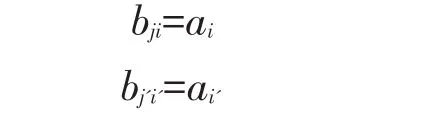
这使得ai=ai'，从而有i=i'.同样的，若j和j'同为偶数，也必有i=i'.这时，bij=bi'j'=bij'，根据构造法，B中同一行各数互异，则必有j=j'，从而aj=aj'.矛盾.

因此，应有aj=aj'，亦必有j=j'.此时，bij=bi'j'=bij'，而根据构造法，必有i=i'.

综上，若存在（bij，bji）=（bi'j'，bj'i'），则必有i=i'，j=j'.说明B与BT正交.

根据众所周知的结论，B与BT为正交的广义完全拉丁方，则A=4k*B+BT+E为完美幻方.

最后，证明A的保块和性质.事实上，由构造法易知，A中任意二阶方块，对应B中二阶方块4数为ap，4k-1-ap，ap+1，4k-1-ap+1，对应BT中二阶方块4数为aq，4k-1-aq，aq+1，4k-1-aq+1，得A中任意二阶方块4数之和为：

因此A是保块和的.A的幻和为2k*[（4k）2+1]，任意二阶方块4数之和为幻和的1/k.

证毕.

3 讨论

[1]李超.造任意4k阶保块和泛对角线幻方的一组公式[J].韶关学院学报：自然科学版,2006,27(12)：1-5.

[2]李超.造任意4k阶保块和泛对角线幻方的又一组公式[J].韶关学院学报：自然科学版,2007,28(3)：5-9.