带部分风险资产的最优投资问题
樊 涛,陈传钟,马 丽
(海南师范大学 数学与统计学院,海南 海口 571158)
1 引言和模型假定
在保险精算学中,学者们对保险公司的最优投资比例问题越来越感兴趣.因为保险公司不仅投资到货币市场,而且部分投资到股票市场.但是股票市场具有高风险性,所以投资策略和风险管理变得越来越重要.较早研究这个问题的是Browne[1],他考虑的模型是风险资本模型是由经典的Black-Scholes模型刻画,保险公司的风险过程是一个带漂移的Brown运动刻画,得到的结果是在没有负债约束的条件下,不管公司盈余多少,最优投资策略是在风险市场上投资定量的资金.Chi Sang Liu和Hailiang Yang[2]在经典的风险模型基础上,加入风险投资和无风险投资,将保险公司资产分为两部分,一部分是投入股票市场的资产,另一部分投入到证券市场,他们通过HJB方程,得到一个关于最优投资股票市场金钱数量与初始盈余的关系.
本文在经典的Lundberg风险模型的基础上,加入风险投资和无风险投资,将投到风险资产上的比例为b(t),b(t)∈[0 ,1]建立相关的投资模型,将随机控制理论运用到此模型中,解决最优随机控制问题,通过生存概率推导出相关的HJB方程,得到生存概率最大的最优解b(t)与初始盈余之间的关系.
假定在交易过程中没有交易费和税费,假定投资过程中仅有一个风险股票市场和一个无风险证券市场,t时刻的股票价格用pt表示,则pt满足随机微分方程(1)
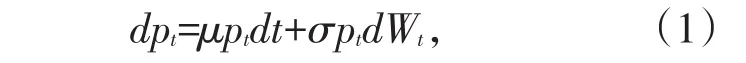
其中μ和σ是正常数,μ表示股票返回的瞬间期望率,σ表示股票价格的易变性,{Wt∶t≥0}是定义在完备化的概率空间(Ω,F,P)上的标准布朗运动,.t时刻证劵价格满足随机微分方程(2)

r0表示利率,假定r0是非负常数.下面我们从经典的Cramer-Lundberg模型出发,假定风险模型(3)


要找到最优投资比例bt,使得保险公司破产概率最小.假定①{btU(t),t≥0}是可测并且是适应过程,且②
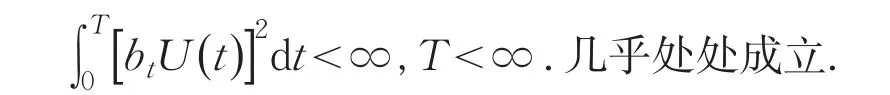
假定①意味着投资者只能依据现有的信息决策,投资者“没有先知先觉”功能,不能准确预测未来价格的变化,假定②的经济意义是投资者不能“恶意透支”[3].
2 最优投资问题的HJB方程
用生存概率

作为目标函数,来求一个投资策略,也就是定出最优投资比例b*(t),使得生存概率最大化[4].
考虑一个很小的区间[0,dt],在这个小时间段内最多只有一个索赔发生,由于索赔到达过程{N(t),t≥0}服从强度为 的泊松分布,所以在[0,dt]上有一次的索赔Y到达的概率为λdt,此时盈余将减少为u-Y,反之无索赔发生的概率为1-λdt+o(dt),盈余将增加为

由全概率公式生存概率δ(u)取期望可以表示成式(6)
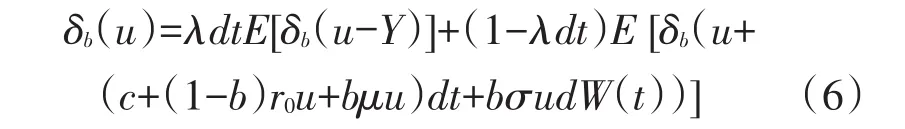
由于δ(u)是连续二次可微的(见Hansperter Schmidli[5])类似于(随机分析与应用Fima C Klebaner[6])中Th4.13的证明,可以对上面式子施加泰勒展开式,得到式(7)



这就得到了最优问题的HJB方程.
3 最优投资问题HJB方程的求解
这里首先可以假定δ(u)严格递增,因为保险公司财富储存越多,保险公司生存概率也就越大,另外假定δ(u)是凹函数,并且索赔密度函数是局部有界的[7].令b*(t)u是在股票市场上的最优投资数量,令

将b*(t)代入HJB方程中,经过一些计算,可以得到

易得t=0时,初始盈余u=0,b(*t)=0,代入HJB方程,得到 cδ′(0)=λδ(0),这就是HJB方程的初始条件,同时若δ(u)是一个解,那么kδ(u)也是它的解,为了简便令δ(0)=1所以初始条件为c=λδ(0)[8].设F(y)表示索赔大小的分布函数,则

对积分项进行计算,令H(t)=1-F(t),用部分积分法则,

下面考虑常见的指数型索赔分布情况,注意到H(u)的表示,假定(fy)=ke-ky,那么F(y)=1-e-ky,H(y)=e-ky这里为了计算方便,令 t(u)= δ′(u ),v(u)=所以


这是一个非线性常微分方程,很容易可以得到方程的初始条件w(0)=0,解出w(u),就可以得到δ(u)和b*(t)U(u),知道比例b(u)了,问题就解决了.下面的任务就是解上面的常微分方程.用两种方法可以解这个常微分方程:第一种方法用有限差分法,用差商代替导数(若步长较小,则有

这样用这个递推公式和初始条件w(0)=0,那么w(u)的数值解就可以得到.
第二种方法,可以用Matlab软件求解微分方程数值解,令k=1,λ=3,μ=0.1,r0=0.04,σ=0.3,c=3.6,最后得到了下列曲线图(见图1).

图1 索赔为指数分布的最优投资策略Fig.1 Claims for the exponential distribution of the optimal investment strategy
可以从图形看出来,当盈余很小的时候,保险公司宁愿把超过盈余的资金都投入到股票市场,下表显示比例几乎是b=1,也就是说保险公司乐意接受高风险的回报来阻止破产和亏损,这是因为风险资产有着更高的漂移系数将导致更高的投资比例,然而当盈余慢慢增大时,投资到股票市场的比例减小,也就是说,盈余越大,保险公司亏损的风险越小,完全可以抵抗住一些索赔数量,保险公司就会乐意持有保守的投资策略,因此保险公司宁愿选择无风险的证劵市场来减少资金的损失.
另外,本文中投资比例和盈余之间的关系图形,与2004年Liu[2]得到的一个投资数量与盈余之间的关系图形吻合较好,并且从此图更能看出,人们投资的比例在0.65以上,这超出了百分之五十,这能够说明我们大多数投资者都是风险爱好者,才会在盈余越来越大的时候还是会把过多的资产投入到风险市场中,这正与实际吻合,同时给保险公司管理者和风险投资者更好地投资策略组合.
4 本文的经济意义
为了提高保险公司的支付能力,考虑将保险公司的资金用于投资,其中包括风险投资和无风险投资两部分,从得出的最优策略随参数u的变化关系,这说明合理的选取u对最优投资策略的变化至关重要,对于保险公司的稳定经营业相当关键,本文的结论对实际运营具有启发性的意义.
[1]Browne S.Optimal Investment Policies for a Firm with a Random Risk Process:Exponential Utility and Minimizing the Probability of Ruin[J].Mathematics of Operations Research,1995,20(2):937-958.
[2]Liu C S,Yang H L.Optimal investment for an insurer to minimize its probability of ruin[J].North American Actuarial Journal,2004,8(2):11-31.
[3]Yang H,Zhang L.Ruin theory with interest incomes[J].Statistics and Finance,1999,55(2):355-369.
[4]Schmidli H.On minimizing the ruin probability by investment and reinsurance[J].The Annals of Applied Probability,2002,12(3):890-907.
[5]Hanspeter S.Stochastic Control in Insurance[M].London:Springer-Verlag,2008:48-49.
[6]Klebaner F C.Introduction To Stochastic Calculus With Applications[M].London:Imperial College Press,2005:105-106.
[7]Schmidli H.Optimal proportional reinsurance policies in a dynamic setting[J].Scandinavian Actuarial Journal,2001,11(1):55-68.
[8]Browne S.Survival and Growth with Liability:Optimal Portfolio Strategies in Continuous Time[J].Mathematics of Operations Research,1997,22(2):468-493.

