Buck-Boost变换器输出纹波电压的PSPICE仿真分析

钟久明，韦建德

（海南师范大学 物理与电子工程学院，海南 海口 571158）

Buck-Boost变换器是最基本的DC-DC变换器电路拓扑结构之一.该变换器电路结构简单、能方便实现负电压输出、工作可靠，因此广泛地应用于各类电力电子及其传动装置中[1].

输出纹波电压是开关变换器的重要性能指标，因而滤波参数的确定是进行直流开关变换器设计最为基本内容之一，而滤波参数的确定又建立在能量传输模式分析的基础之上.而目前关于Buck-Boost变换器新型拓扑结构[2]以及控制方式[3]等方面的研究较为丰富，关于能量传输及纹波电压方面的研究却鲜有涉及.文献[4]在总结实验现象的基础上对Buck-Boost变换器的能量传输过程进行了深入分析，并得出了有别于传统分析的系列结论，并从实验的角度对得出的结论进行了验证.极大的丰富与完善了直流开关变换器相关理论.然而，由于寄生及杂散参数的影响，实验结果与理论分析往往存在较大的差别，而建立在数学模型基础之上的仿真分析则能在最大程度上与理论分析相吻合，而且与电路实验相比，仿真分析简单经济且参数调整灵活方便、适应范围宽，是进行电路分析强有力的辅助设计工具.

PSPICE软件能方便地绘制电路图形、具有丰富的电路模拟仿真功能、强大的图形后处理和元器件符号制作功能；它的用途非常广泛，被认为是通用电路模拟程序中最优秀的软件之一，因而在电子设计自动化领域获得广泛应用[5].因此，本文将在理论分析基础上运用PSPICE仿真软件对Buck-Boost变换器的输出纹波电压进行仿真验证，为其设计与应用准备理论基础.

1 能量传输模式

首先将文献[4]中Buck-Boost变换器能量传输模式的相关结论总结如下：

将最小电感电流ILV与输出平均电流IO相比较，进一步将连续导电模式（CCM）细分为完全电感供能模式（CISM，对应ILV＞IO）与不完全电感供能模式（IISM，对应ILV＜IO），而且此临界电感LK为[4]：

其中RL为负载电阻，Vi为输入电压，VO为输出平均电压，f为开关频率.LC为Buck-Boost变换器CCM与DCM的临界电感，d为占空比.当电感L＞LK时，变换器工作在CISM；反之则处于IISM.

2 各种模式下的输出纹波电压

Buck-Boost变换器工作在CCM之CISM时，输出纹波电压表达式为[1，4]

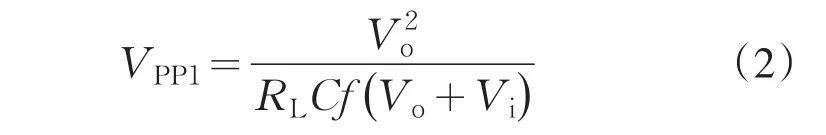
其中C为滤波电容.由（2）式可知，纹波电压与电感无关，而与输入电压、负载电阻、开关频率均成反比关系.

Buck-Boost变换器工作在CCM之IISM时，输出纹波电压为[4]

运用数学知识可知：当电感L＜LK时，VPP2在LC＜L＜LK范围内随着L的增加而减小，且当L=LK时为最小值，即

Buck-Boost变换器工作在CCM之IISM时，输出纹波电压为[5]

同样地，由数学知识并对比（5）式可知：当L=LC时，VPP3取得最小值，且

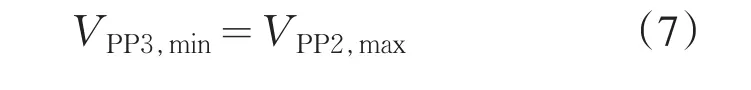
3 输出纹波电压的仿真验证

下面运用PSPICE仿真工具对上节所列结论进行仿真验证.

3.1 仿真图形文件

建立仿真图形文件见图1.L6

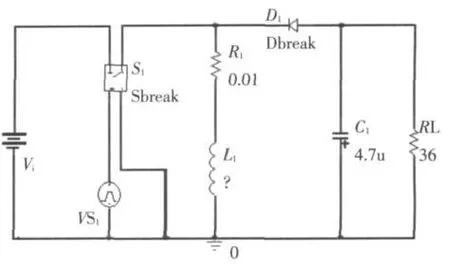
图1 仿真电路图形文件Fig.1 Diagram file of simulation circuit

其中Vi为电源电压，VS1为脉冲电压源，S1为PWM控制开关，D1、L1、C1和RL分别为续流二极管、储能电感、输出滤波电容及负载电阻.

给定Buck-Boost变换器的参数为：Vi=12V，VO=18V，RL=36Ω，IO=0.5A，f=80kHz，C=4.7μF.考虑到电感的寄生电阻并使电路仿真收敛，在电感回路中串入一小电阻R1=0.01Ω.

脉冲电压源VS1的模型参数设定：脉冲周期PER=12.5us、低电平V1=-0.2V、高电平V2=10V、延迟时间TD=0.1ns、上升时间TR=0.1ns、下降时间TF=1ns.

由于PSPICE元件库中无PWM控制器的仿真模型，所以建立图1所所示的开环控制方式图形文件，因此脉冲电压源VS1的脉冲宽度参数PW只能根据输出平均电压手动调整，具体方法如下：

对于某一给定的电感值，首先设定占空比的理论计算值为脉冲宽度参数PW，然后进行试仿真，查看输出平均电压与设定值之间的误差，直至该误差小于某一规定的期望值（如0.1%），方视为有效仿真结果，然后改变电感取值，重复以上试探、比较输出电压、调整占空比的过程，最后完成所有电感参数下的仿真.

3.2 仿真分析及结果

根据式（2）有CCM/DCM的临界电感为：

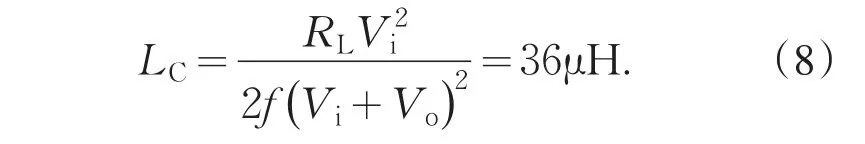
同理，根据式（2）有CISM/IISM的临界电感：LK=LC/d=36/（8/12.5）=56.3μH.

根据以上分析可知，当电感值L＞56.3 μH时，变换器工作在CCM-CISM模式.现分别取电感值L1=100 μH、L2=80 μH、L3=60 μH进行仿真，电路电感电流与电容电压典型波形（以L=60 μH波形为例）见图2.

图2 L3=60μH时的电感电流与电容电压波形Fig.2 Inductor current and output voltage of Buck-Boost converters when L3=60μH

从图2可以看出：当L.＞LK时，最小电感电流大于输出平均电流（IO），即处于CISM模式；在开关管关断期间，电感向负载供能同时给电容充电，电容电压近似线性上升.

分别取电感值L4=50μH、L5=40μH、L6=35μH进行仿真，电路电感电流与电容电压典型波形（以L=35μH的波形为例）见图3.

从图3可以看出：当L=L5=35μH时，最小电感电流满足0＜ILV＜0.5A，变换器工作在CCM-IISM模式；在开关管关断期间，能量的传输分为两个阶段：iL＞IO时，电感给电容充电并给负载供电、电容电压近似线性上升；当iL＜IO时，电感和电容同时为负载供电，电容放电、电容电压线性下降.传统分析认为，Buck-Boost变换器工作于CCM时，开关管关断期间，电容C一直被充电，电容电压一直近乎线性上升.仿真结果表明，传统分析存在明显错误.

分别取电感值 L7=30μH、L8=20μH、L9=10μH进行仿真，电路电感电流与电容电压典型（以L=20μH的波形为例）波形见图4.

图3 L5=35μH时的电感电流与电容电压波形Fig.3 Inductor current and output voltage of Buck-Boost converters when L5=35μH

图4 L8=20μH时的电感电流与电容电压波形Fig.4 Inductor current and output voltage of Buck-Boost converters when L8=20μH

从图4可以看出：当L.＜LC=20μH时，最小电感电流等于零（小于输出平均电流IO），即处于DCMIISM模式；在开关管关断期间，能量传输分为两个阶段：当iL＞IO时，电感给电容充电并给负载供电、电容电压近乎线性上升；当iL＜IO时，电感与电容同时给负载供电，电容放电、电容电压近乎线性下降.

综合以上所有电感取值，可得仿真结果见图5.

由图5可知，当电感取值满足L＞LK＞LC时（分别取60、80和100μH），最小电感电流均大于输出平均电流（0.5A），即变换器工作于CISM-CCM模式.仿真结果表明，在该模式下，变换器的输出纹波电压不变.

当电感取值满足LC＜L＜LK时（分别取35、40和50μH），最小电感电流均大于零且小于输出平均电流（0.5A），即变换器工作于IISM-CCM模式.仿真结果表明，在该模式下，变换器输出纹波电压随着电感取值减小而单调增大.而传统分析认为，连续模式下，变换器输出纹波电压与电感取值无关，这显然是错误的.

图5 最小电感电流、纹波电压与电感关系曲线Fig.5 The minimum Inductor current and output voltage vs L for given Vi、RL、C and f

当电感取值满足 L＜LC＜LK时（分别取30、20、10μH），最小电感电流均等于零，结合仿真波形（见图5）可知，变换器工作于IISM-CCM模式.仿真结果表明，在该模式下，变换器输出纹波电压随着电感取值减小而单调递增.

需要指出的是，临界电感LC、LK的仿真值略小于理论计算值，而纹波电压则略大于理论计算值.这主要是由于仿真过程中需根据输出平均电压不变而手动调节占空比加之读数误差而导致的结果.

综上所述，仿真结果与理论分析吻合得很好，表明了理论分析和推导的正确性.

4 结论

开关频率、输入电压、电容和负载电阻给定的Buck-Boost变换器，当L＞LK时，变换器处于CISMCCM，且其输出纹波与电感值无关.当LC＜L＜LK时，变换器处于IISM-CCM，且其输出纹波随着电感取值减小而增大.当 L＜LC＜LK时，变换器处 IISMCCM，且其输出纹波随电感值的减小而递增.

PSPICE仿真结果与理论分析吻合得很好，验证了理论分析的正确性及PSPICE仿真的有效性和优越性，为变换器分析和设计提供了一种有效的仿真工具.

[1]张占松,蔡宣三.开关电源的原理与设计[M].北京：电子工业出版社,2008.

[2]任小永,唐钊,阮新波,等.一种新颖的四开关Buck-Boost变换器[J].中国电机工程学报,2008,28(21)：15-19.

[3]毕玉春,汪小锋,刘立生.具有斜坡补偿的Buck-Boost变换器的碰撞分岔现象及混沌[J].哈尔滨理工大学学报,2010,15(3)：77-81.

[4]刘树林,刘健,钟久明.Buck-Boost变换器的能量传输模式及输出纹波电压分析[J].电子学报,2007,10(5)：838-84.

[5]周润景,张丽娜,王志军.Pspice电子电路设计与分析[M].北京：机械工业出版社,2011.