基于因子分析的中国地区商品价格波动研究

石洪景

（福建江夏学院 经济贸易学院，福建 福州 350108）

商品之所以有价格源于其有使用价值，商品价格一般由人力价格和材料价格构成[1].商品价格水平的波动对企业生产、社会消费、宏观经济政策的制定与实施和微观经济政策的调整都会产生重要的影响.作为生产企业和经销企业必须关注商品价格的波动，以便及时制定有针对性的生产、营销措施[2].商品价格的高低不但关系到买卖双方的切身利益，也直接影响到消费者对某些商品的购买意愿以及购买数量的多少，商品价格是消费者购买心理中最敏感的因素，商品价格通过影响消费者的购买心理进而作用于消费者的购买行为[3].在市场竞争中，商品价格越来越多地被广大商家作为一种有力的市场竞争武器来使用，通过商品价格的调控来获取市场竞争的优势[4].消费者在购买商品时，会通过与市场上同类商品比较、自己的心理定位、相对性比较、商品的外观特征、消费者自身的感受经验、企业定价的动机和企业声誉等方面关注商品价格的公正性，并对商品价格做出主观的公正价值判断，其价值判断直接影响到消费者的购买决策[5].

由此可知，商品价格不但关系到生产企业、经销企业等供应方的利益，也关系到购买者的心理感知、经济利益获取、消费价值的最大化等问题.然而随着国际化进程的加快、市场化程度的不断提高等，商品价格会受到国家政策、市场因素等的影响而使其自身的波动成为一种常态[6].因而有必要找出影响商品价格波动的主要因素和商品价格波动水平的高低，从而为有针对性地采取相应措施来保障商品价格的稳定性提供依据.

1 商品价格波动分析及其评价指标设计

1.1 商品价格波动分析

商品价格的波动往往是多种因素综合作用的结果，如市场环境因素、企业自身因素、成本因素、国家政策方面的因素以及市场的供求平衡规律等都会在不同程度上影响到商品价格的波动[6].周凯歌等[7]通过选取冶金、化工、食品和纺织四个行业的2003年1月至2008年4月的相关指标数据进行研究分析，发现能源价格与商品价格之间存在长期均衡关系，商品价格明显受到能源价格的变化影响，且能源价格对不同行业的商品价格的冲击程度有所不同.解学祖[2]认为商品价格水平的高低不仅取决于商品价值量的大小，也受到市场上商品供求关系的影响.托马斯·郝尔伯林等[8]通过研究发现新兴国家的飞速发展、生物燃料的兴起、供应增加迟缓、商品之间的价格传导以及低利率和美元贬值等都是推动商品价格上涨的重要力量.朱国华[9]认为要考察商品价格暴涨的原因可从根本原因、物质原因、金融原因、技术原因以及基础性支撑原因等几个方面着手分析.谭顺[10]认为商品的价格是由商品价值决定的基础价格与商品使用价值决定的调整的价格共同构成，即商品价格是一个复合性价格.许亚萍[11]通过对北京市零售业商品价格的考察，发现商品价格受到许多因素的影响，而其中消费者群体的构成、销售模式的变化、供应链等因素对零售业商品价格的波动起着至关重要的作用.刘萌芽等[12]认为市场供求关系对商品价格的影响只是一个幌子，真正决定商品和劳务交易价格的是其背后的实力，如垄断、产权专有权、信息不对称等因素.

1.2 评价指标设计

从以上学者的相关研究可知，影响商品价格波动的因素复杂多样.为此，在借鉴相关学者已有研究的基础上，结合商品价格的内涵，笔者从构成商品的各个具体产品类别出发来选取相应的指标内容，即从商品大类中选取食品类、家庭用品类、医疗保健品类、生产建筑品类以及精神产品类作为评价商品价格高低的依据.在确定指标选取的内容及范围后，为了便于统计分析与研究，需要找出具体的分析指标，根据研究内容的要求，选取了食品、纺织品、家用电器及音像器材、文化办公用品、日用品、体育娱乐用品、交通通信用品、中西药品及医疗保健用品、书报杂志及电子出版物和建筑材料及五金电料等10个具体的分析指标.

2 商品价格波动评价指标的数据来源

在确定好10个具体分析指标的基础上，为了准确科学地反映出商品价格波动的内涵，评价指标的数据必须符合科学性、完备性、可靠性、可获得性且可比性的原则[13].因此，笔者选取了2010年全国各地区的商品零售价格分类指数（见表1），以此作为评价商品价格波动的数据指标，并对这10个数据指标做如下变量假设：食品为χ1，纺织品为χ2，家用电器及音像器材为χ3，文化办公用品为χ4，日用品为χ5，体育娱乐用品为χ6，交通通信用品为χ7，中西药品及医疗保健用品为χ8，书报杂志及电子出版物为χ9，建筑材料及五金电料为χ10.

3 商品价格波动的因子分析

3.1 因子分析方法内涵

因子分析最早是由心理学家Chales Spearman于1904年提出的，其基本思想是将实际观测到的多个数据指标用少数几个潜在的指标（因子）的线性组合来表示，也即通过具体指标测评抽象因子的一种分析方法；在因子分析过程中，需根据相关性的大小把变量分组，使得同组内的变量的相关性较高，而不同组的变量相关性较低；因子分析的具体步骤如下：（1）根据研究的具体问题来选取原始变量；（2）对原始变量进行标准化处理并求出其相关阵，分析变量之间的相关性及其是否适合于因子分析；（3）构造因子变量；（4）通过旋转使因子变量具有更好的解释性；（5）计算因子变量的得分；（6）根据因子得分情况做进一步的分析[15].

3.2 因子分析可行性检验

因子分析的前提要求是原有变量之间应具有较强的相关关系，一般在因子分析时需首先对因子分析的条件即原有变量是否相关进行研究，目前通过可采用的检验方法有：计算相关系数矩阵、计算反映像相关矩阵、巴特利特球度检验（Bartlett Test of Sphericity）和KMO检验（Kaiser-Meyer-Olkin）[16].笔者通过运用SPSS16.0软件对原始变量进行KMO和巴特利特球度检验，检验结果见表2.

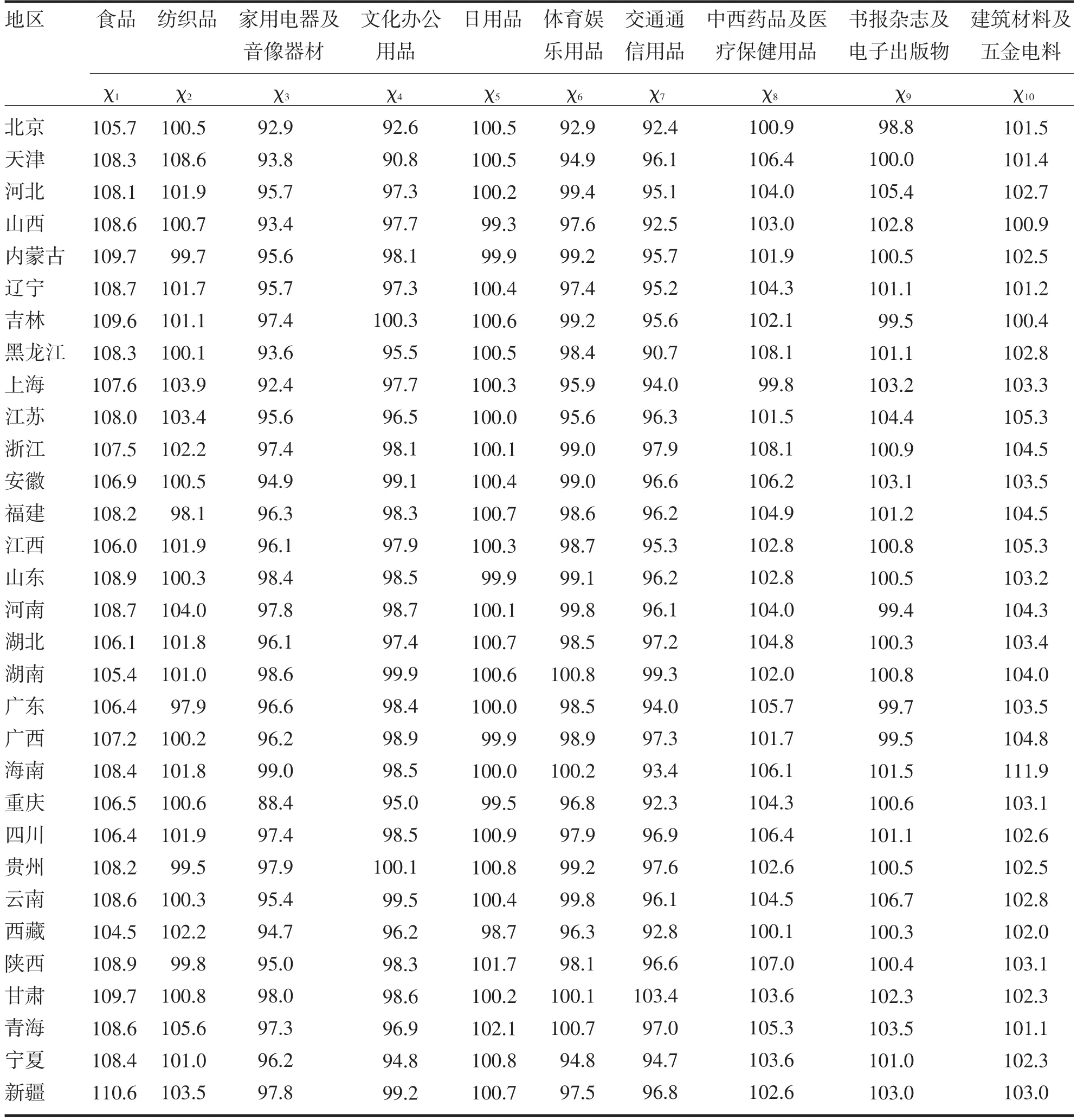
表1 2010年各地区商品零售价格分类指数（上年=100）Tab.1 The regional classification index of retail price in 2010（last year=100）

从表2可知，KMO统计量的值为0.587，巴特利特球度检验的卡方统计量的值为92.948，显著性水平为Sig.＝0.000，小于给定的显著性水平0.05，说明表1中的各项指标数据具有较大的相关性，适合作因子分析.

表2 KMO检验和球度检验结果Tab.2 The result of KMO and Bartlett's test

3.3 提取因子

对原始指标数据通过采用主成分分析法提取特征值大于1的因子，得到以下特征值与方差贡献表（见表3）.表3中第一列是因子编号，以后三列组成一组，每组中数据项的含义依次是特征值、方差贡献率和累计方差贡献率.从表3可知，前4个特征值大于1，同时，这4个公共因子的累计方差贡献率为70.872%，即解释了原有变量总方差的70.87%，总体上原有变量的信息丢失较少，因子分析效果较理想.因此，可以运用前4个主因子进行商品价格波动的因子分析.

表3 特征值与方差贡献表Tab.3 The eigenvalues and variance contribution

3.4 因子命名与解释

通过采用方差极大法对因子载荷矩阵进行正交旋转，使得因子具有命名解释性，得到结果见表4.表4中公共因子与原有变量之间的相关程度由因子载荷值表示，正值表示正相关、负值表示负相关，因子载荷值越高，说明该因子与该变量的相关程度越高，包含该变量的信息也越多.从表4可知，因子1在家用电器及音像器材χ3、文化办公用品χ4、体育娱乐用品χ6、交通通信用品χ7四个指标上有较大的载荷，反映出器材、办公娱乐、及交通通信用品的商品价格情况，且可解释原有变量总方差的27.70%，可以命名为家庭用品因子；因子2在纺织品χ2、建筑材料及五金电料χ10两个指标上有较大的载荷，反映出纺织品和建筑类商品价格情况，且可解释原有变量总方差的15.71%，可以命名为纺织品和建筑因子；因子3在日用品χ5、中西药品及医疗保健用品χ8两个指标上有较大的载荷，反映出日用类和医疗卫生类商品价格情况，且可解释原有变量总方差的14.28%，可以命名为日用和医疗保健因子；因子4在食品χ1、书报杂志及电子出版物χ9两个指标上有较大的载荷，反映出饮食类和期刊类商品价格情况，且可解释原有变量总方差的13.18%，可以命名为食品和读物因子.

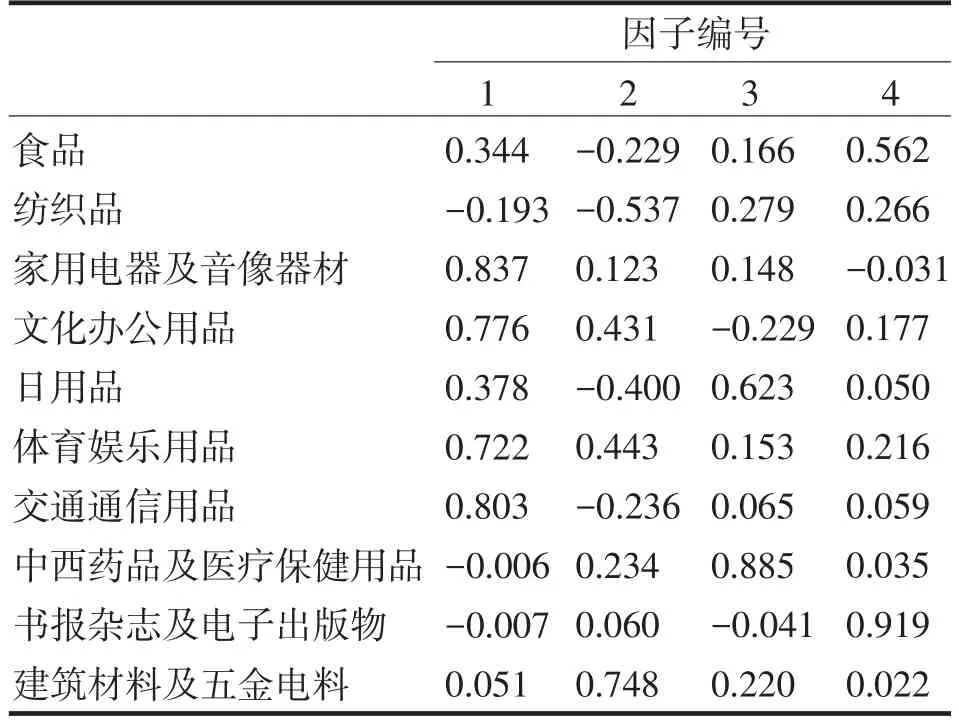
表4 旋转后的因子载荷矩阵Tab.4 Rotated component matrixa

从表4可以容易地写出因子分析模型：

χ1=0.344F1-0.229F2+0.166F3+0.562F4+ε1；

χ2=-0.193F1-0.537F2+0.279F3+0.266F4+ε2；

χ3=0.837F1+0.123F2+0.148F3-0.031F4+ε3；

χ4=0.776F1+0.431F2-0.229F3+0.177F4+ε4；

χ5=0.378F1-0.400F2+0.623F3+0.050F4+ε5；

χ6=0.722F1+0.443F2+0.153F3+0.216F4+ε6；

χ7=0.803F1-0.236F2+0.065F3+0.059F4+ε7；

χ8=-0.006F1+0.234F2+0.885F3+0.035F4+ε8；

χ9=-0.007F1+0.060F2-0.041F3+0.919F4+ε9；

χ10=0.051F1+0.748F2+0.220F3+0.022F4+ε10；

其中F1、F2、F3、F4分别代表4个公共因子.

3.5 计算因子得分

通过采用回归法估计因子得分系数，并得到因子得分系数矩阵，见表5.

表5 因子得分系数矩阵Tab.5 Component score coefficient matrix

根据表5可以写出以下因子得分函数：

F1=0.081χ1-0.071χ2+0.326χ3+0.263χ4+0.149χ5+0.197χ6+0.357χ7-0.124χ8-0.139χ9-0.107χ10；

F2=-0.154χ1-0.303χ2-0.024χ3+0.183χ4-0.279χ5+0.229χ6-0.265χ7+0.227χ8+0.103χ9+0.523χ10；

F3=0.035χ1+0.167χ2+0.041χ3-0.224χ4+0.392χ5+0.061χ6-0.049χ7+0.668χ8-0.088χ9+0.209χ10；

F4=0.386χ1+0.190χ2-0.147χ3+0.080χ4-0.083χ5+0.095χ6-0.087χ7-0.015χ8+0.764χ9+0.048χ10；

把原始指标数据代入以上因子得分函数，可求出各个因子的具体分数；同时，各个地区的因子综合得分可用公式F=0.27703F1+0.15710F2+0.14278F3+0.13181F4求出并进行排序（见表6）.

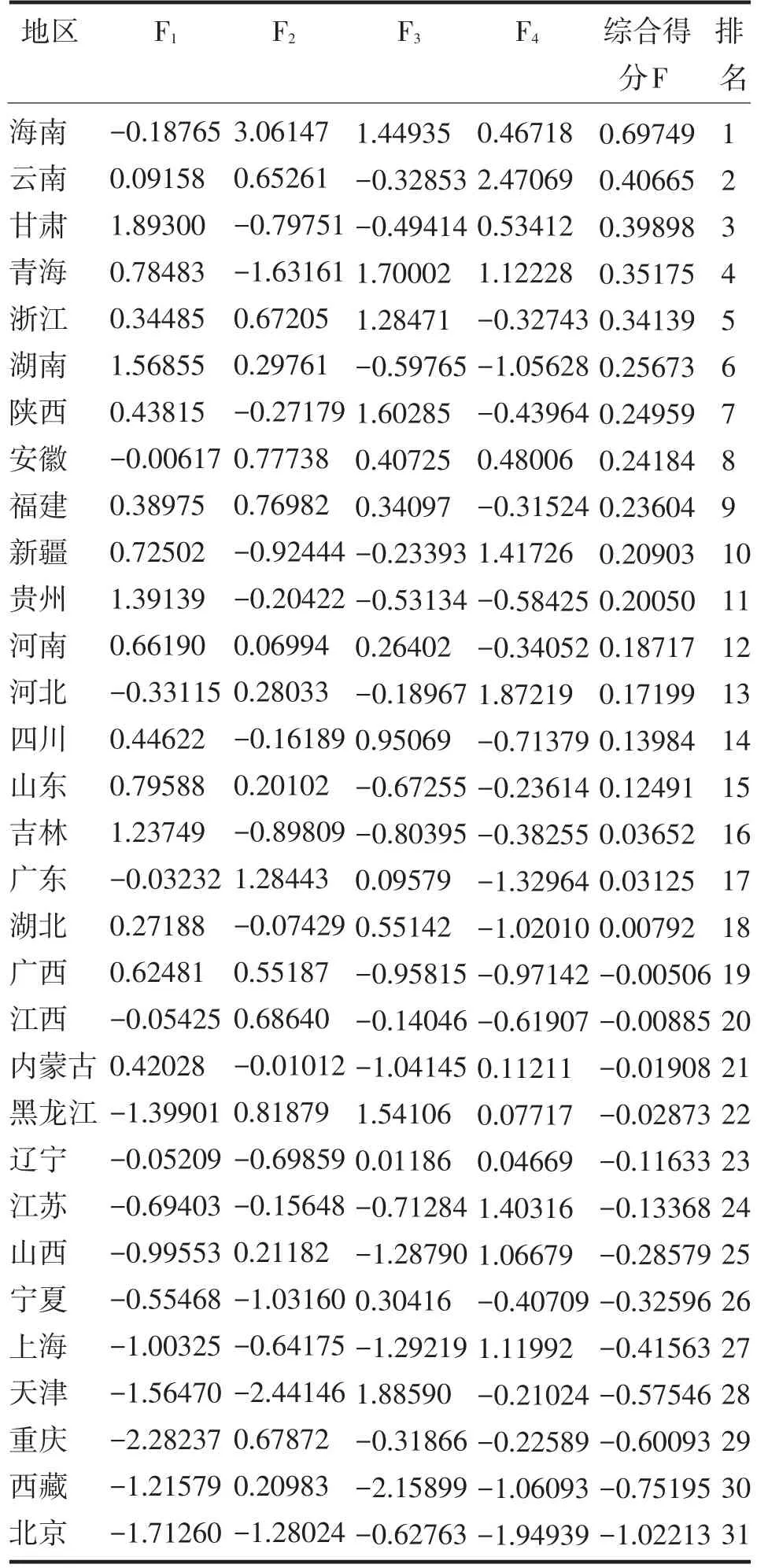
表6 各地区商品零售价格因子得分及排序1）Tab.6 The factor score and ranking of the regional retail price

从表6可知，海南地区的商品价格波动水平最高，其次为云南、甘肃、青海、浙江、湖南、陕西、安徽等地区，而北京地区的商品价格波动水平最低.

4 研究结论

通过对2010年全国各地区的商品零售价格分类指数运用因子分析方法分析，试图找出影响商品价格波动的主要因素并分析，得出如下结果.

1）商品价格波动的主要影响因素可归纳为4个因子，这4个因子总共解释了70.87%的全部原始指标信息.其中第一个因子可称为家庭用品因子，主要反映出器材、办公娱乐、及交通通信用品的商品价格情况，且可解释原有指标数据总方差的27.70%；第二个因子可称为纺织品和建筑因子，主要反映出纺织品和建筑类商品价格情况，且可解释原有变量总方差的15.71%；第三个因子可称为日用和医疗保健因子，主要反映出日用类和医疗卫生类商品价格情况，且可解释原有变量总方差的14.28%；第四个因子可称为食品和读物因子，主要反映出饮食类和期刊类商品价格情况，且可解释原有变量总方差的13.18%.

2）通过计算各因子得分、总得分，并对因子综合得分进行排序，可知商品价格波动水平较高的地区有海南、云南、甘肃、青海、浙江、湖南、陕西、安徽等，而北京地区的商品价格波动水平最低.

[1]李宁.简析商品价格[J].中国市场,2010(13)：85-89.

[2]解学祖.商品价格的动态分析[J].哈尔滨工程大学学报,2001,22(1)：92-96.

[3]祝海波.基于商品价格的消费者心理反应模式研究[J].商业时代,2006(8)：39-47.

[4]鞠志萍.市场竞争的有力武器-商品价格[J].商场现代化,2006(3)：156-157.

[5]郝春霞.消费者对商品价格的公正性与不公正性的分析[J].科技情报开发与经济,2007,17(28)：149-151.

[6]李新红.浅析商品价格的影响因素与对策[J].商业文化,2010(4)：223-224.

[7]周凯歌,彭艳,徐兴华.能源价格变动对商品价格的影响[J].价格月刊,2010(11)：6-9.

[8]托马斯·郝尔伯林,瓦莱丽·默瑟-布莱克曼,凯文·程.世界商品价格上涨的原因及其影响[J].江西社会科学,2008(6)：252-256.

[9]朱国华.资源性商品价格暴涨原因探析[J].贵州财经学院学报,2006(5)：1-6.

[10]谭顺.商品价格的复合决定因素分析[J].特区经济,2006(12)：50-51.

[11]许亚萍.北京市零售业商品销售价格影响因素分析[J].生产力研究,2009(16)：135-137.

[12]刘萌芽,王洋,李妮.论商品价格不是供求决定而是POWER说了算[J].经济研究导刊,2010(10)：8-9.

[13]翁玲玲,高辉灵,陈秀兰,等.海峡西岸经济区各市经济发展水平评价[J].福建农林大学学报：哲学社会科学版,2010,13(5)：23-26.

[14]中华人民共和国国家统计局.中国统计年鉴—2011[M].北京：中国统计出版社,2011.

[15]何晓群.现代统计分析方法与应用[M].北京：中国人民大学出版社,2007：350-362.

[16]薛薇.统计分析与SPSS的应用[M].北京：中国人民大学出版社,2011：317-341.