矩形基板上LED芯片阵列热分析

曾海，郭震宁，陈俄振，胡治伟

（华侨大学 信息科学与工程学院，福建 厦门361021）

发光二极管（LED）作为21世纪的新一代绿色能源，以其高效、节能、长寿命、稳定性好等优势获得广泛的应用.在LED的实际使用中，芯片温度的变化对光电转换效率、光通量、寿命等性能会产生巨大的影响［1-2］.对多芯片的封装系统而言，不仅要考虑各芯片的温度，还要考虑各芯片温度是否一致.因此，如何进行多LED芯片封装模型中的热设计成为LED应用中一个研究重点.Kim等［3］介绍了1个芯片、2个芯片和4个芯片的热设计方案.Yovanovich等［4］研究了电子封装中多芯片的扩散热阻.Muzychka等［5-6］根据扩散热阻，获得能够预测芯片质心过余温度（CTEC）和芯片平均温度的理论.为了使各芯片温度相同，刘胜等［7-8］设计并优化了由3W和5W两种不同功率封装而成的80W路灯.本文利用局部模拟和理论论证的方法，对芯片阵列热分布进行研究.

1 偏心热源理论

1.1 单一热源理论

Muzychka等［5-6］通过分离变量法得到单一热源在基板上的过余温度.其表达式为

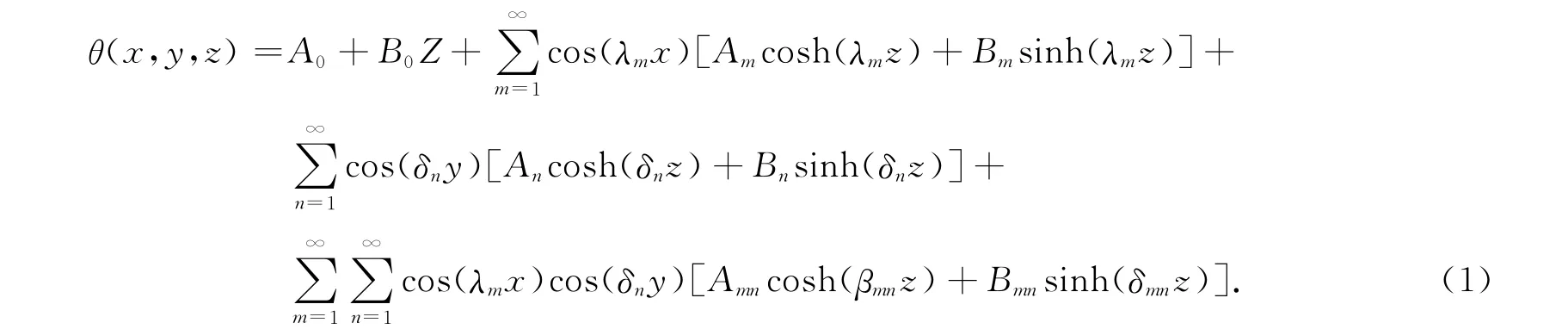
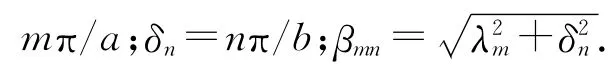
在z＝t1平面，根据相应的热边界条件，得到Fourier系数Bi，即

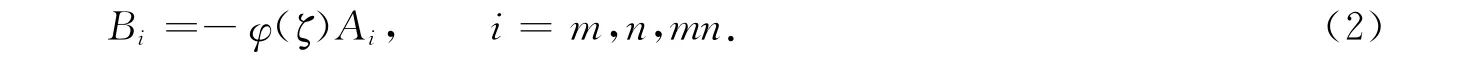
式（2）中：扩展系数φ（ζ）为

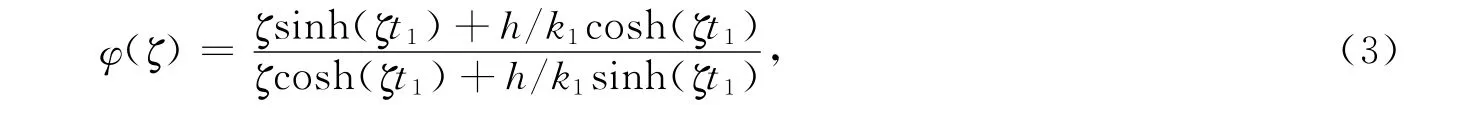
式（3）中：ζ分别用λm，δn或βmn代替.

对z＝0平面上相应的热边界条件，进行Fourier级数展开，得到Fourier系数Am，An，Amn，有

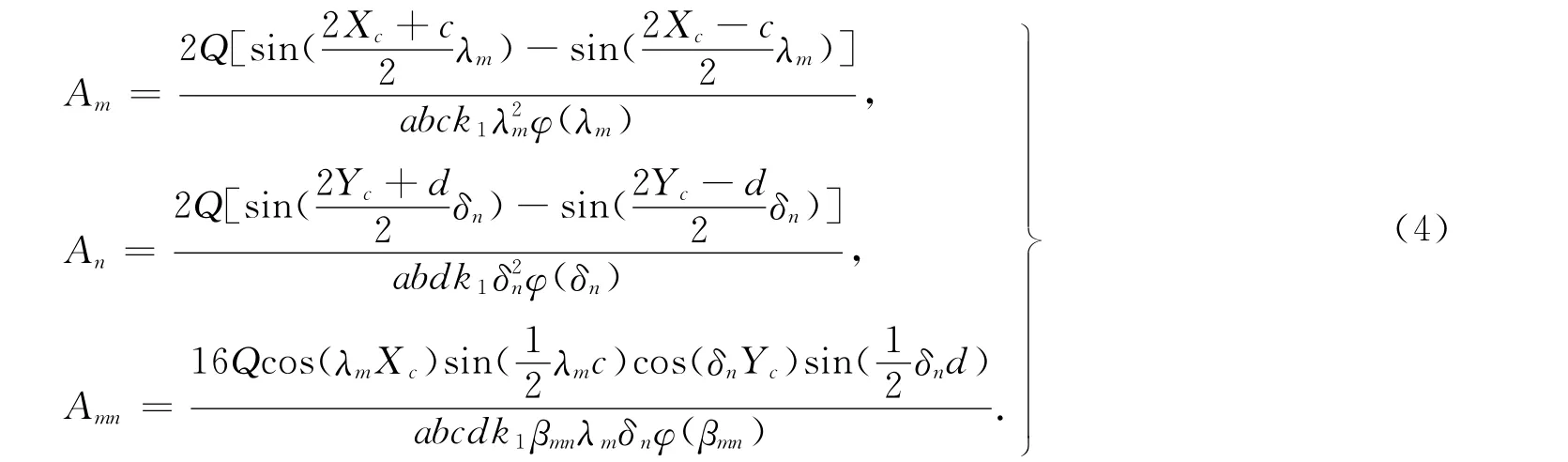
式（4）中：Xc，Yc为热源质心的坐标.

最后，得到均匀热流解，即

1.2 多热源理论

包含多个热源的系统的过余温度，可由式（1）线性叠加得到.因此，对于有n′个热源的系统，热源所在平面的过余温度可表示为

式（7）中：θj（x，y）为第j个热源的过余温度，即

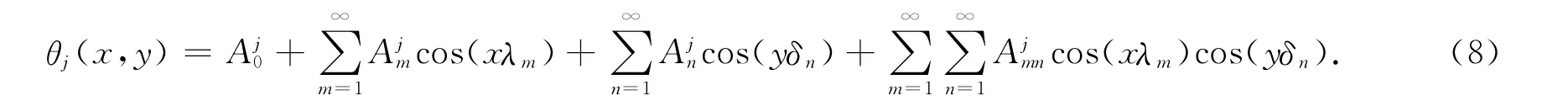
由式（7）可得第i个热源CTEC的表达式，即

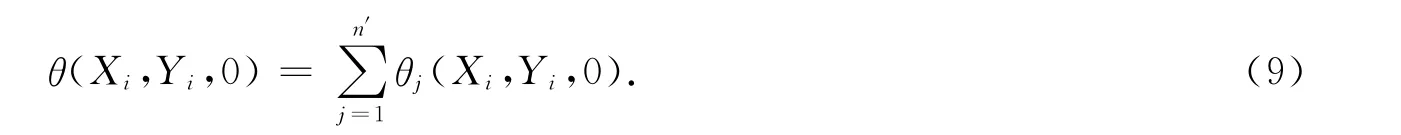
式（9）中：（Xi，Yi）为第i个热源质心的坐标.

1.3 m′×n′阵列LED芯片热分布理论

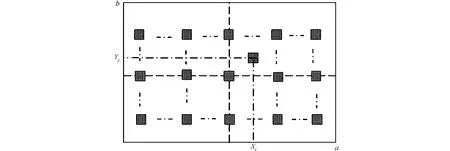
图1 m′×n′阵列的LED分布Fig.1 LED distribution in m′×n′array

LED芯片是1个热源.因此，前文关于单一热源和多热源的理论适合LED芯片的封装模型.m′×n′阵列LED芯片封装模型，如图1所示.图1中：基板长为a，宽为b；X轴方向每行有m′个芯片，Y轴方向每列有n′个芯片；芯片大小和功率都相同，且功率用Q表示；（Xi，Yj）为第i，j个芯片质心坐标.

为了更直观地理解单一热源的过余温度，将式（8）改写为

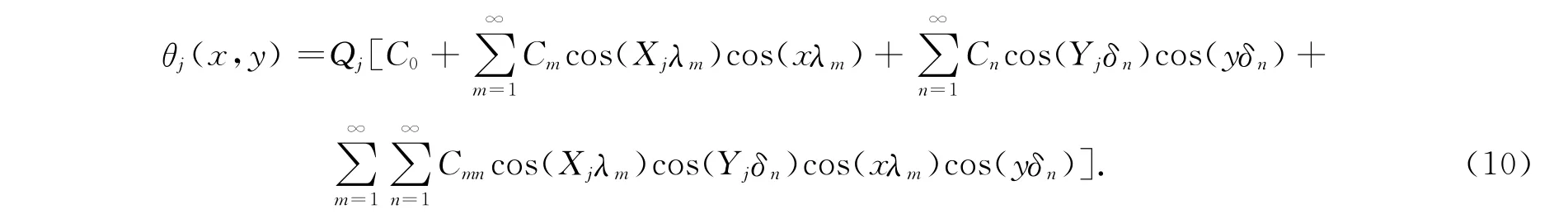
A0＝QjC0＝Cmcos（Xjλm），＝Cncos（Yjδn），＝Cmncos（Xjλm）cos（Yjδn）.C0，Cm，Cn和Cmn是与芯片位置无关的量.

由图1，并根据式（7），（10），通过计算和化简，可得到m′×n′阵列的LED芯片过余温度表达式，即

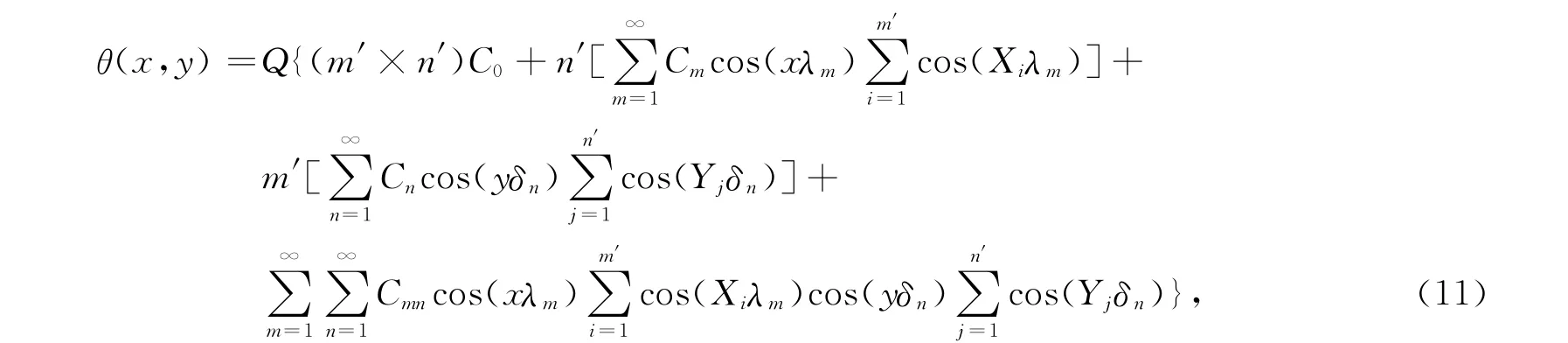
则第i，j个的CTEC为

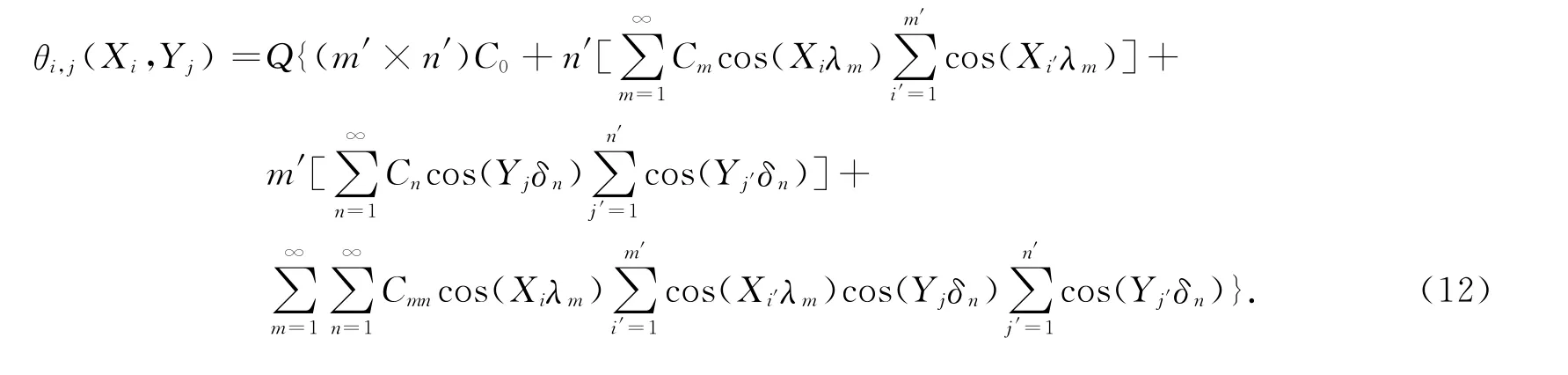
2 数值模拟实验与理论论证

2.1 数值模拟实验与预测

以芯片之间的距离为变量，建立如图2所示的模型.芯片对称分布在基板上，且芯片之间的间距相等，X轴方向，芯片之间的间距为x；Y轴方向，芯片之间的间距为y.因芯片是阵列排布，故图2中只给出X轴方向的芯片排布.

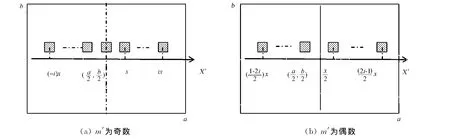
图2 芯片的X坐标Fig.2 Xcoordinates of the chip

把Xi和Yj的表达式带入式（12），有

鉴于x和y相互独立的特性，对式（12）中1个变量进行模拟，模拟所用等式为

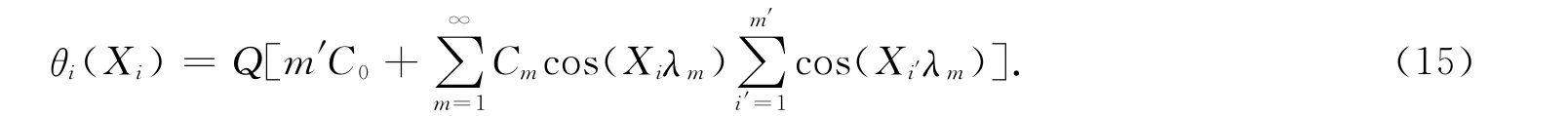
对式（15）用Mathcad软件进行模拟.在模拟的过程中，根据m′的不同值，使用式（13）中相关的表达式.模拟实验，选取以下参数：基板厚度（t1）为0.002m；基板大小（a）为0.18m；基板大小（b）为0.18m；对流换热系数（h）为20W·（m2·K）-1；基板热导率（k1）为180W·（m·K）-1；注入功率（Q）为1W；芯片大小（c）为0.002m；芯片大小（d）为0.002m.

图3为不同m′值的芯片θ（x）的示意图.由图3模拟结果可以看出：当芯片之间的间距（x）分别为0.036 0，0.030 0，0.025 7，0.022 5，0.020 0，0.018 0时，不同m′值中各芯片的θi（Xi）相同.对于这些间距值，又可写成x＝a／m′.于是，猜想对于m′×n′阵列的LED芯片，当芯片之间的间距为x＝a／m′，y＝b／n′时，各芯片的CTEC相同.下文，通过理论来论证.

2.2 理论论证

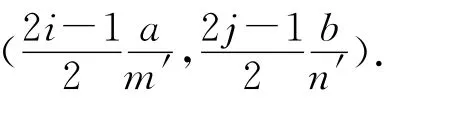
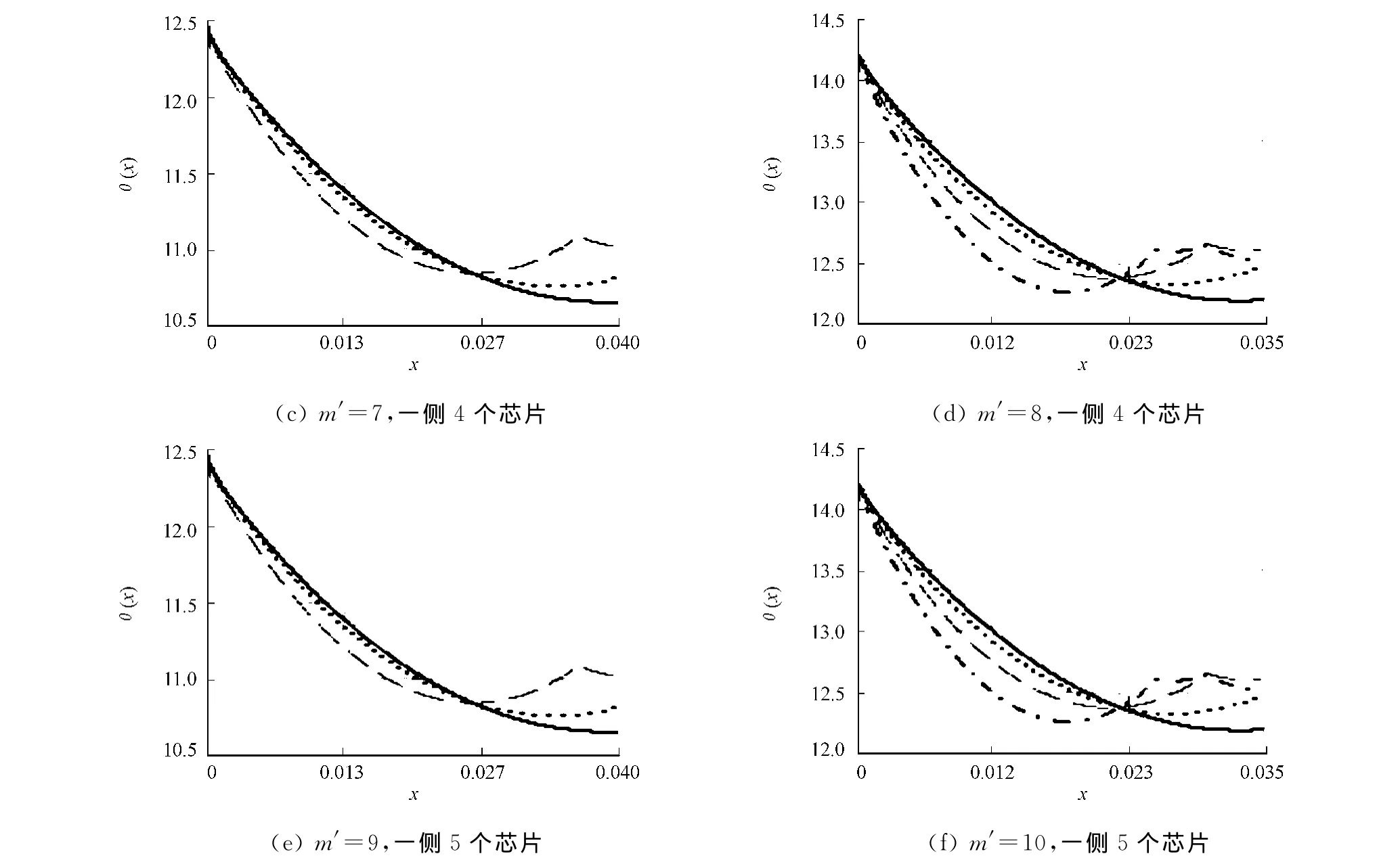
图3 不同m′值的芯片θ（x）的示意图Fig.3 θ（x）schematic of the different m′value of chips

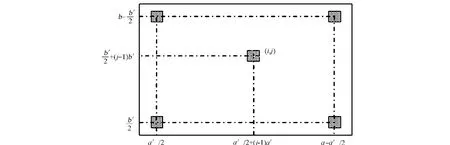
图4 芯片的坐标系Fig.4 Coordinates of the chip

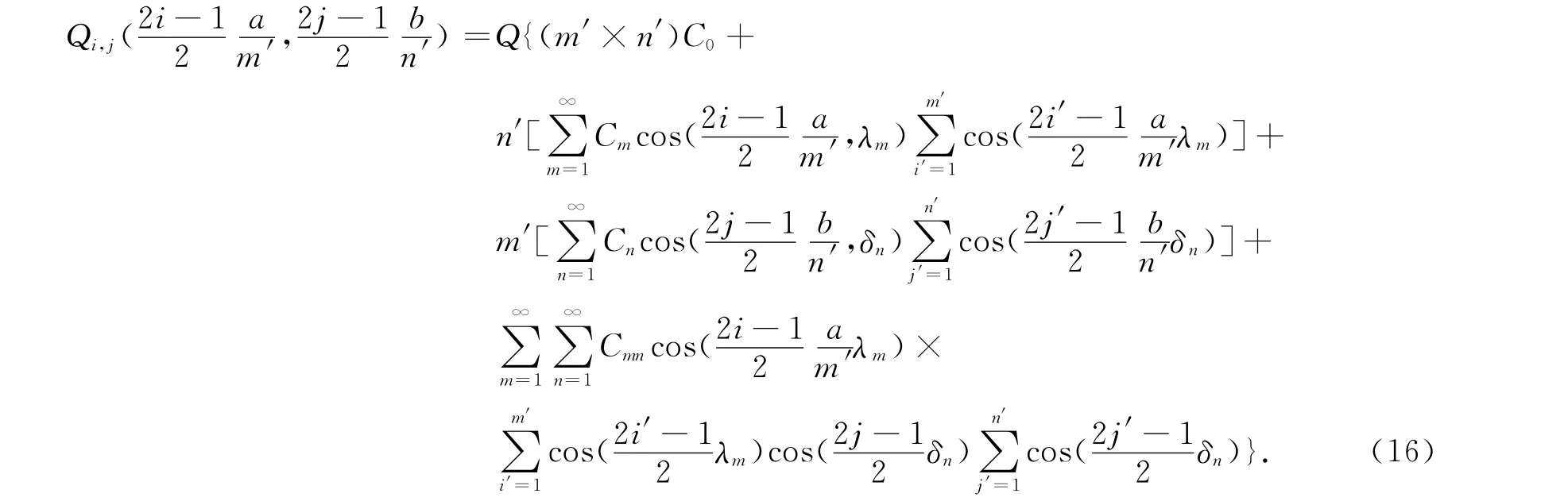
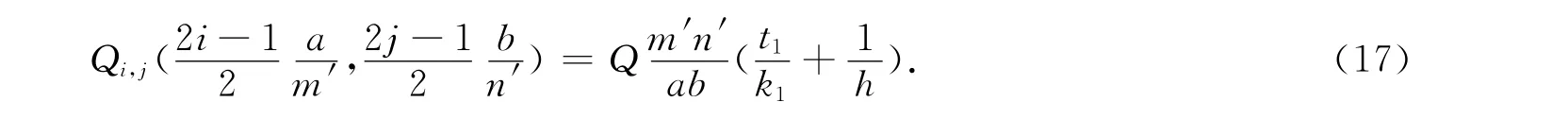
定义1个新的量Qs，其为基板面积与芯片总功率之比（m2·W-1），或者单功率芯片所占的基板面积.有

由此，式（15）可化为

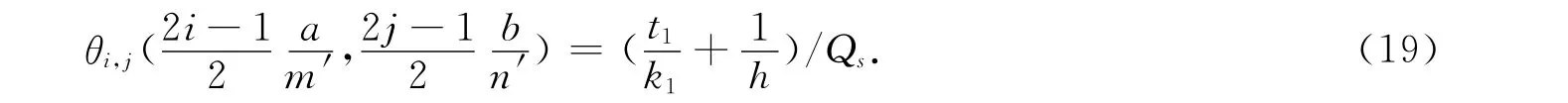
2.3 数值模拟论证与分析

用Mathcad软件对上述理论结果进行数值模拟论证，并以式（11）结合式（13）或式（14）进行模拟.模拟所用数据：基板厚度（t1）为0.002m；对流换热系数（h）为20W·（m2·K）-1；基板热导率（k1）为180W·（m·K）-1；功率（Q）为1W；芯片大小（c）为0.002m；芯片大小（d）为0.002m.模拟结果图，如图5所示.

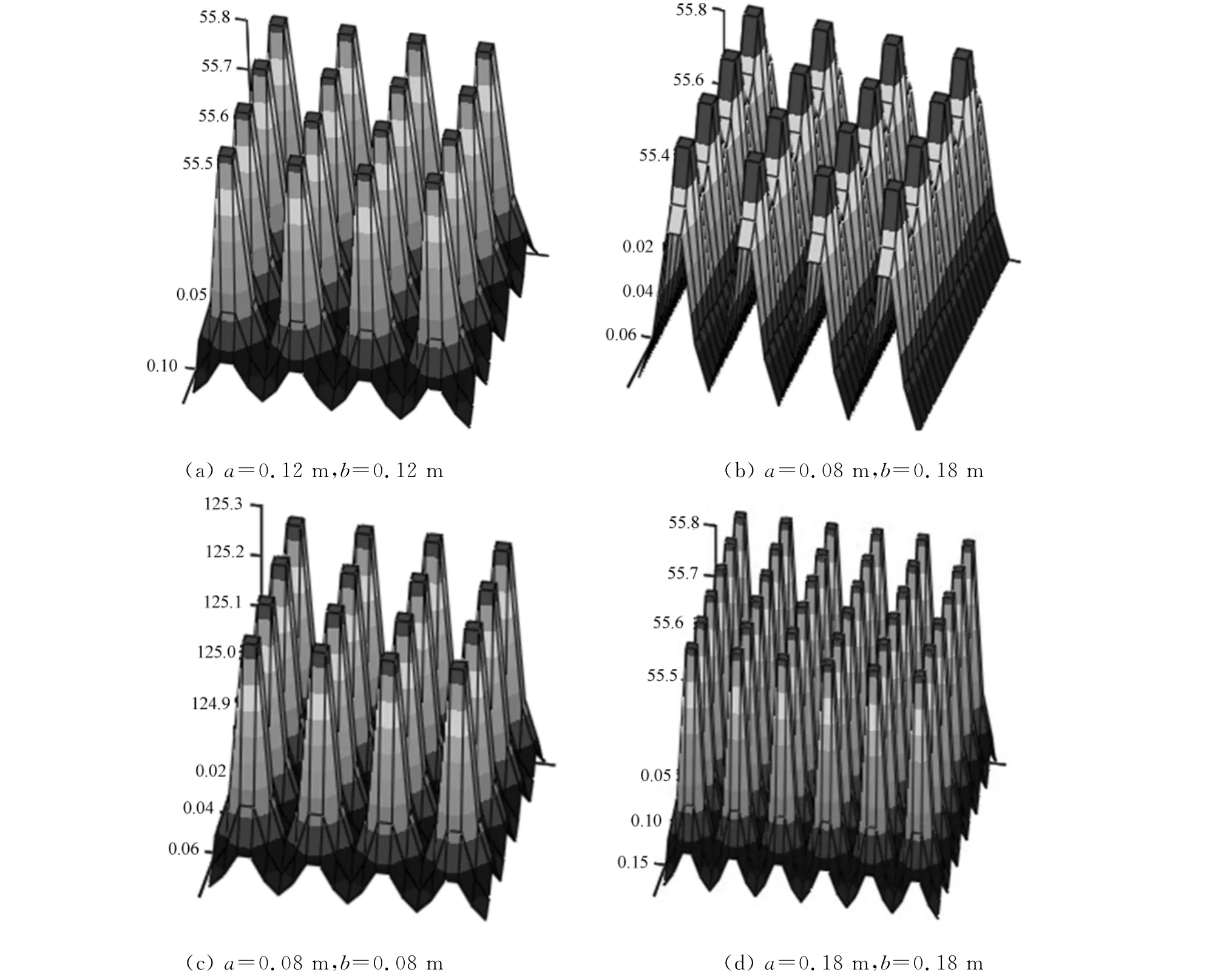
图5 模拟结果图Fig.5 Simulation results chart

利用式（17）对图5（a）～5（c）所示情况进行计算.取芯片质心坐标为（0.015，0.015）（图5（a），5（b），5（d）所示）和（0.01，0.01）（图5（c）所示）；由计算得到的过余温度θ（0.015，0.015）＝55.57℃，θ（0.01，0.01）＝125.03℃.对比可知：理论计算与数值模拟结果一致.

3 结论

通过本文研究分析可知，m′×n′阵列LED芯片以芯片间距（a／m′，b／n′）在尺寸为a×b的矩形基板上对称排布时，各芯片的CTEC都相同.根据该方案的模型，获得了CTEC的表达式.该表达式指出：1）在基板面积相同的条件下，CTEC的大小与基板的长宽比无关，此结果有利于基板上散热器的设计；2）CTEC与Qs成反比，因而能在一定程度上预知芯片的温度，也可根据对芯片CTEC不同的实际要求选择Qs.

［1］ NARENDRAN N，GU Y.Life of LED-based white light sources［J］.IEEE／OSA Journal of Display Technology，2005，1（1）：167-171.

［2］ NARENDRAN N，GU Y，FREYSSINIER J P，et al.Solid-state lighting：Failure analysis of white LEDs［J］.Journal of Crystal Growth，2004，268（3／4）：449-456.

［3］ KIM L，SHIN M W.Thermal analysis and design of high power LED packages and systems［C］∥Proceedings of SPIE.San Diego：［s.n.］，2006：681-687.

［4］ CULHAM J R，YOVANOVICH M M，LEMCZYK T F.Thermal characterization of electronic packages using a three-dimensional fourier series solution［J］.Journal of Electronic Packaging，122（3）：233-239.

［5］ MUZYCHKA Y S，CULHAM J R，YOVANOVICH M M.Thermal spreading resistance of eccentric heat sources on rectangular fux channels［J］.ASME Journal of Electronic Packaging，2003，125（2）：178-185.

［6］ MUZYCHKA Y S.Influence coefficient method for calculating discrete heat source temperature on finite convectively cooled substrates［J］.IEEE Transactions on Components and Packaging Technologies，2006，29（3）：636-643.

［7］ LUO Xiao-bing，CHENG Ting，XIONG Wei，et al.Thermal analysis of an 80Wlight-emitting diode street lamp［J］.IET Optoelectronics，2007，1（5）：191-196.

［8］ CHENG Ting，LUO Xiao-bing，HUANG Su-yi，et al.Thermal analysis and optimization of multiple LED packaging based on a general analytical solution［J］.International Journal of Thermal Sciences，2010，49（1）：196-201.