自适应粒子群优化BP神经网络的变压器故障诊断

付宝英，王启志

（华侨大学 机电及自动化学院，福建 厦门361021）

变压器的运行状态直接影响着电力系统的安全，对变压器故障做到及时、准确的诊断，可有效减少故障隐患所带来的安全事故.传统的故障诊断方法，如四比值法、三比值法、电协研法等，由于存在编码不全、诊断准确率较低而被日益淘汰.BP神经网络具有良好的自学习能力和强大的非线性映射能力［1］，在变压器故障领域发挥着较大作用.但BP神经网络存在易陷入局部极点、学习速率较难准确选取等问题，采用新型智能算法对其进行改进成为一种较可行的方法.粒子群算法作为最有潜力的神经网络训练方法，具有收敛速度快、全局搜索能力强等优点［2-3］，用来优化BP神经网络，可以有效弥补BP神经网络的不足.杨道武等［4］使用带惯性权重的粒子群算法优化BP神经网络；王晓霞等［5］将惯性权重和收缩因子同时引入粒子群算法中用于优化BP网络的权值和阈值.然而大多改进粒子群算法都是针对惯性权重的改进，忽略了粒子群其他参数对算法性能的影响.本文在分析粒子群各参数对算法性能影响的基础上，对粒子群的惯性权重和加速因子进行非线性调整，提出自适应粒子群算法用于优化BP神经网网络的权值和阈值，将其应用于变压器故障诊断中.

1 自适应粒子群算法的策略制定

1.1 标准粒子群算法［6］

假设粒子的群体规模为N，那么在D维的搜索空间中，第i个粒子的位置可表示为xi＝（xi，1，xi，2，…，xi，D），速度可表示为vi＝（vi，1，vi，2，…，vi，D），其中i＝1，2，…，N.若将第i个粒子目前所搜索到的最优位置记为pi＝（pi，1，pi，2，…，pi，D），将群体目前所搜索到的最优位置记为pg＝（pg，1，pg，2，…，pg，D），那么在每次迭代过程中，粒子i在第d维子空间中的速度vi，d和位置xi，d的更新公式表示为

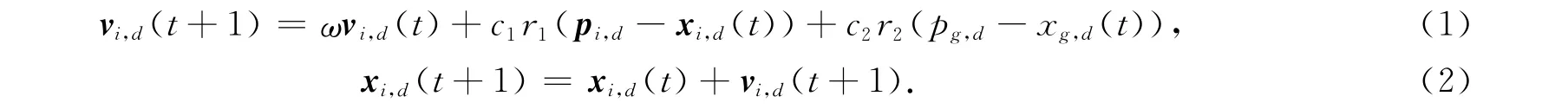
式（1）～（2）中：ω为惯性权重；c1，c2为非负的加速常数，也称加速因子或学习因子；r1，r2为［0，1］之间的随机数；i＝1，2，…，N；d＝1，2，…，D.

在粒子群算法中，一般会对速度向量vi，d进行最值限制，当vi，d＞vmax时，取vi，d＝vmax；当vi，d＜-vmax时，则取vi，d＝-vmax.

1.2 粒子群算法的参数分析及自适应粒子群算法的提出

选取一个合适的惯性权重值（ω）可以平衡粒子全局搜索能力和局部搜索能力，增强粒子群的寻优性能.在粒子群寻优的初期，可以采用较大的惯性权值，以获得较好的全局搜索能力；而在寻优的后期，则采用较小的惯性权值，以达到尽快收敛的目的.因此，惯性权重的调整策略可以制定为一个逐步递减的调整方案.同时，对于适应度值较小的粒子，可以适当加大粒子的权重值，以激励这些较好粒子在粒子更新中所起的积极作用，而对于适应度值较大的粒子，则可以削弱这些粒子在粒子更新中所起的作用.由此建立惯性权重的调整公式为

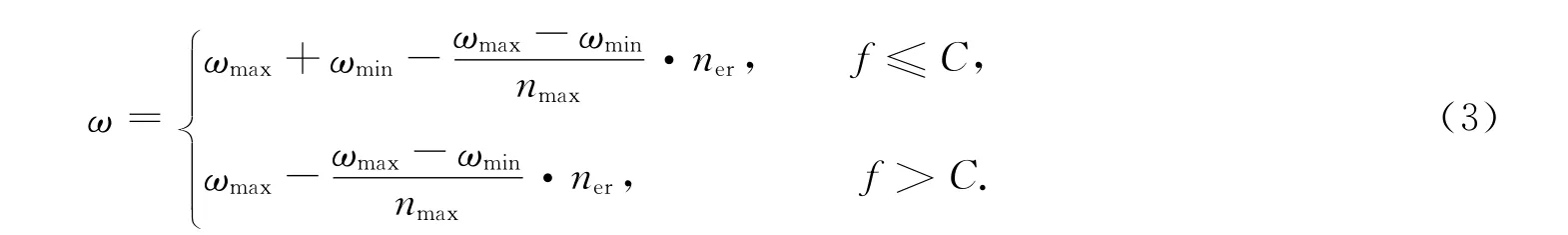
式（3）中：ωmax，ωmin为设定的权重最大值和最小值；nmax为粒子的最大迭代次数，ner为粒子的当前迭代次数；f为粒子的当前适应度值；C为粒子的当前最优适应值.

在粒子群算法中，除了惯性权重的这个重要参数外，加速因子在算法性能中也起着较为重要的作用.合适的加速因子搭配可以加快粒子的搜索速度，减少粒子陷入局部极小的可能.在寻优初期，可采用较大的c1和较小的c2，以确保每个粒子都能做到较全面的局部搜素，而在粒子的后期则应该适当减小c1、增大c2，以促进粒子之间的相互交流，达到尽快收敛的目的.因此，可采用c1非线性递减策略，并构建c1，c2之间的非线性搭配关系c2＝a-c1+b，实现c1随迭代次数逐渐减小，c2随迭代次数逐渐增加的目的.建立的加速因子调整公式表示为

式（4）中：cmax，cmin为设定的参数最大值和最小值；a，b为正常数.

2 自适应粒子群优化BP神经网络的流程

在自适应PSO算法优化BP神经网络时，首先要确定神经网络的拓扑结构，并根据网络的拓扑结构来确定粒子的维数.在PSO优化BP时，神经网络权值和阈值总个数应等于粒子的维数.其次，在BP网络中，网络不断调整权值和阈值是以误差均方值为基准的，那么在PSO优化BP时，就应建立误差均方值与PSO适应度函数的对等关系.故PSO-BP中的适应度函数可表示为

式中：yi，j，y′i，j分别为样本的理想输出值和实际输出值；m为网络输出层的个数；N为输入样本的个数.

将上述2个关键点解决后就可以进行自适应粒子群算法的寻优，其具体流程有如下8个步骤.

1）初始化算法参数，需要初始化的参数有最大迭代次数nmax、最大速度vmax、群体规模N、惯性权重ωmax和ωmin、加速因子cmax和cmin，以及随机初始的位置向量和速度向量等.

2）根据实际求解的问题确定BP神经网络的拓扑结构，建立网络初始模型；并根据网络的拓扑结构，计算粒子的维数，如5-12-4的三层BP网络，则粒子维数为124.

3）输入网络的训练样本，将初始化的位置向量作为当前全局最优值映射到网络的权值和阈值中，计算网络的实际输出值和误差均方值，并以误差均方值作为粒子群的适应度函数.

4）按照粒子群的更新公式进行粒子速度和位置的更新.

5）进行迭代运算，将当前最优适应度值与粒子群的局部最优值pbest进行比较，若当前最优适应度值优于pbest时，则取代当前局部最优值，完成粒子群的局部极值更新.

6）将当前全局最优值与粒子群的全局最优值gbest进行比较，若当前全局最优值优于gbest时，则取代gbest，完成粒子群的全局极值更新.

7）将全局最优粒子中的位置向量映射到BP神经网络的权值和阈值中.

8）将测试样本输入粒子群优化后的BP神经网络中，分析测试样本的输出结果，检验算法的性能.

3 基于自适应PSO-BP变压器故障诊断

3.1 故障诊断系统的建立

变压器的故障特征气体有5种：H2，CH4，C2H6，C2H4，C2H2；对应的故障类型有4种：高能量放电、低能量放电、高温过热和中低温过热；建立BP神经网络的拓扑结构为5-14-4.参考文献［7-9］搜集了80组样本数据，以其中的52组作为训练样本，28组作为测试样本，将这52组训练样本输入故障诊断系统，完成系统的训练，再使用28组测试样本检验系统的性能.建立的自适应PSO-BP变压器故障诊断系统，如图1所示.

图1 自适应PSO-BP的变压器故障诊断系统Fig.1 Transformer fault diagnosis system of adaptive PSO-BP

由图1可知，该系统包含了三大模块：归一化处理模块、自适应粒子群优化BP神经网络模块和故障编码输出模块.故障样本经归一化处理后，进入自适应PSO-BP模块进行学习和训练，得出故障编码，进而诊断出故障类型.

3.2 自适应PSO-BP的参数设置

粒子群优化算法中，参数的初始化对网络的性能有较大的影响，在仿真分析中，需要经过多次尝试方可确定比较满意的初始值.经过多次仿真试验，设置最大迭代次数nmax为200，最大速度vmax为1.0，群体规模N为40，神经网络结构为5-14-4，粒子维数D为144（维数计算＝5×14+14×4+14+4），惯性权值的最大值ωmax为0.7，最小值ωmin为0.3，加速因子的最大值cmax为2.5，最小值cmin为0.5.速度和位置的初始化选择公式v＝a+（b-a）×nmax和X＝c+（d-c）×nmax，设置参数a＝c＝0.5，b＝d＝-0.5.

3.3 变压器故障诊断结果及分析

将52组训练样本输入自适应粒子群优化的BP神经网络中进行网络训练，确定网络最优的权值和阈值，并使用28组测试样本进行性能测试，评估粒子群优化后的网络性能.28组样本经训练后的自适应PSO-BP变压器故障系统的输出结果，如表1所示.

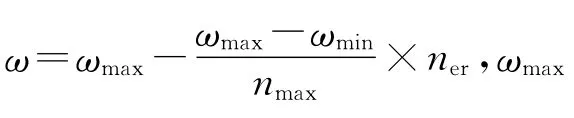
分析三组诊断结果可知：使用自适应PSO优化BP神经网络进行变压器的故障诊断时，只有2组出现诊断错误，其余26组诊断结果都与实际故障类型相吻合，诊断的准确率达到了92.86%；在标准粒子群优化的BP神经网络故障诊断中，有5组数据出现诊断错误，诊断的准确率只达到82.14%，误差均方值也较大；而BP神经网络的诊断准确率只有78%左右，诊断效果较差.

仿真自适应PSO-BP的训练误差曲线和标准PSO-BP的训练误差曲线，如图2所示.图2中，n为迭代次数，σ为误差均方值.由图2可知：在自适应PSO优化BP神经网络中，粒子群的迭代寻优效果良好，前25步左右可以迅速减小网络的训练误差均方值至0.048左右，在140步左右就基本达到了平衡，使σ减小到了0.03左右.而在标准粒子群优化BP神经网络中，刚开始随着迭代次数的增加，网络的误差均方值也能较快减小，但之后在较长迭代次数内都下降缓慢，在120步时达到σ的最小值0.17，之后就不再发生变化，整体动态性能没有自适应PSO-BP好.自适应PSO-BP的最终误差均方值为0.03左右，标准PSO-BP的最终误差均方值为0.17左右，是自适应PSO-BP误差均方值的5.67倍，寻优误差较大.由此可见，自适应PSO-BP可以获得较好的寻优效果和较快的收敛速度，并有效减小训练误差.

表1 28组测试数据仿真结果Tab.1 Simulation results of 28groups of test data

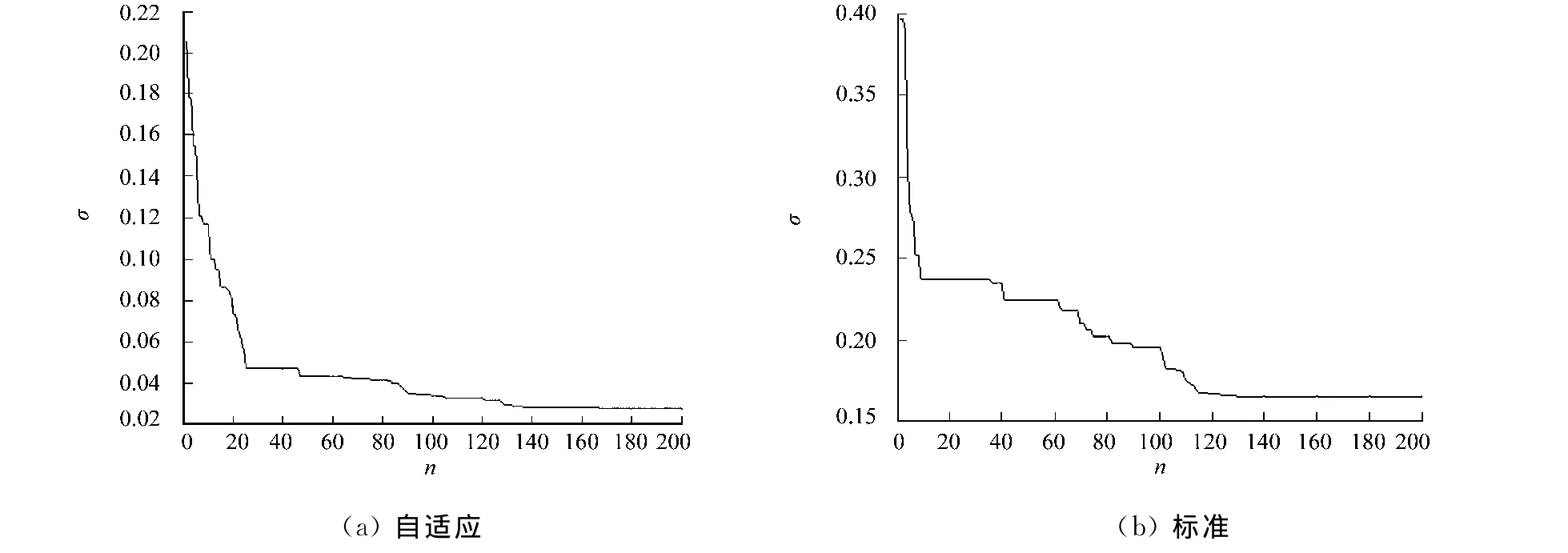
图2 PSO-BP的训练误差曲线Fig.2 PSO-BP training error curve

4 结束语

针对BP神经网络对变压器故障诊断准确率不高的问题，提出使用粒子群算法优化BP神经网络；并针对粒子群算法的参数特征，提出基于惯性权重和加速因子非线性调整的自适应粒子群算法.建立自适应粒子群优化BP神经网络的变压器故障诊断系统，通过仿真对比分析，验证该系统能较大程度地提高变压器故障诊断的准确率.

［1］ 回敬，律方成.将具有可信度的BP神经网络应用于变压器故障诊断［J］.电力科学与工程，2010，26（2）：9-13.

［2］ SHI Y，EBERHART R C.A modified particle swarm optimizer［C］∥IEEE International Conference on Evolutionary Computation.Alaska：Achorage，1998：69-73.

［3］ 崔长彩，李兵，张认成.粒子群优化算法［J］.华侨大学学报：自然科学版，2006，27（4）：343-346.

［4］ 杨道武，李海如，向卫东，等.基于改进PSO-BP混合算法的电力变压器故障诊断［J］.电力科学与技术学报，2011，26（1）：99-103.

［5］ 王晓霞，王涛.基于粒子群优化神经网络的变压器故障诊断［J］.高电压技术，2008，34（11）：2362-2367.

［6］ EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory［J］.Insititute of Electrical and Electronics Engineers，1995（10）：39-43.

［7］ 刘晓津.基于支持向量机和油中溶解气体分析的变压器故障诊断［D］.天津：天津大学，2007：53-55.

［8］ 吴宏崎，周妮娜，王春英.基于RBF神经网络的变压器故障诊断及MATLAB仿真研究［J］.科学技术与工程，2010，10（5）：1249-1251.

［9］ 程加堂，熊伟，段志梅，等.灰色神经网络在变压器故障诊断中的应用［J］.高压电器，2010，46（8）：56-58.