多产品运输问题的建模及优化算法设计

郑爱萍，金福江

（华侨大学 信息科学与工程学院，福建 厦门361021）

运输问题最早由Hichcock［1］于1941年提出的，是解决产地和销地之间如何合理安排物资调运方案的一类问题 .许多实际的问题如生产存储等问题也可以通过相应的变换转为运输模型进行求解，因此研究运输问题具有相当重要的实际意义.多种产品条件下的运输模型及优化算法研究对降低运输成本，提高企业经济效益具有重要作用.大多数运输问题都是在单一产品、多个生产地、多个销售地模型的基础上对优化方法进行研究，如表上作业法及其推广［2-3］、图上作业法及其他智能算法［4-5］，等等.企业实际的物资运输都是同时运输多种产品，因此要降低运输成本，提高企业经济效益，就需要对多种产品条件下的运输模型及优化算法进行研究.然而，目前有关多种物资运输问题的建模和优化算法研究成果还很少.本文针对现代企业普遍存在有多个生产地、多种产品、多个销售地的运输特点，建立多种产品条件下的物流运输模型.

1 运输问题的优化模型

1.1 目标函数

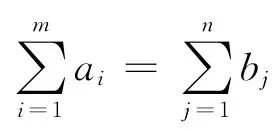
设Ci，k，j为第i（i＝1，…，m）个生产地向第j（j＝1，…，n）个销售地运输第k（k＝1，…，p）种产品的单位运费，则可得到单位运费矩阵为

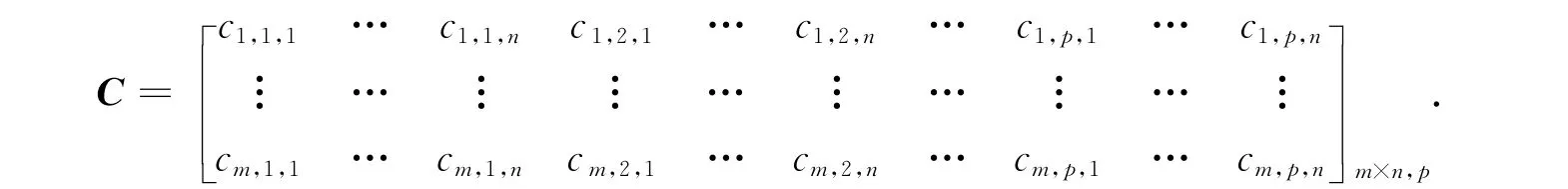
其中：矩阵C的行表示m个不同的生产地，列表示p种产品的n个不同销售地.

设Xi，k，j为第i（i＝1，…，m）个生产地向第j（j＝1，…，n）个销售地运输第k（k＝1，…，p）种产品的产品货运量，则可得到产品货运量矩阵为

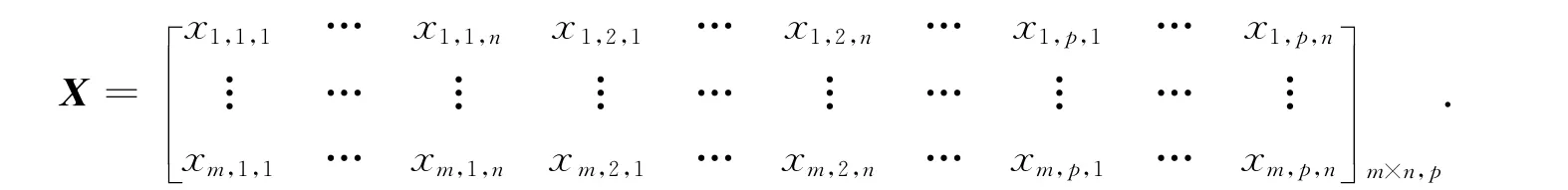
其中：矩阵X的行表示m个不同的生产地，列表示p种产品的n个不同销售地.

对上述两个矩阵进行点乘及求和运算，即可得出多种产品运输问题的优化目标函数为

1.2 约束方程

1）产量约束 .第i个生产地生产的第k种产品被运往r（r≤n）个销售地的货运量等于i产地的k产品的产量，故多种产品运输问题的产量约束方程为

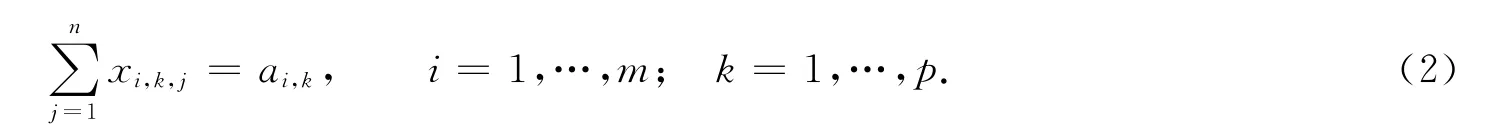
2）销量约束.第j个销售地的第k种产品的销量等于i个生产地运往d（d≤m）销售地k产品的货运量，故多种产品运输问题的销量约束方程为

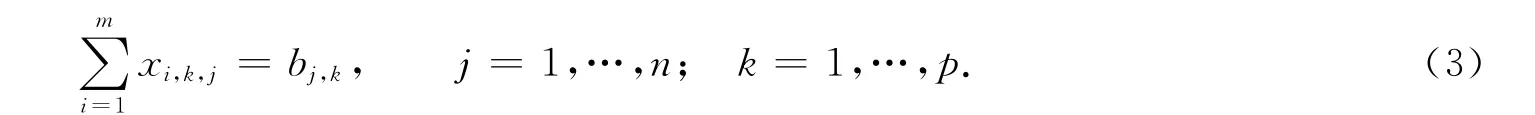
3）变量值的约束 .由变量值的定义可知，其约束方程为

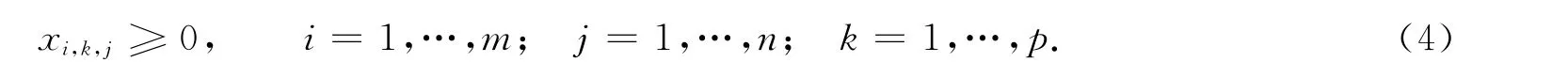
2 遗传算法设计

基本的遗传算法［6］是某一代种群经过对生物基因的复制、变换和变异，产生新一代种群；然后，重复此过程，直到群体或最优点的性能达到满意程度.图1为所设计的遗传算法的流程图，主要有如下8个基本步骤［7］.

1）编码.采取二进制形式进行编码，即将变量值代表的个体表示为二进制串.

2）初始群体的生成 .初始化种群是产生优化问题的一组初始可行解，故文中设定种群的大小为20，采用随机的方式产生初始种群.

3）适应度函数.为了把目标函数转化为求极大值问题，故构造适应度函数为f（x）＝0.95z／10000，则总成本z越小的染色体其适应度越大.

4）约束条件 .由于运输问题的约束条件可转化成只含有｛0，1｝两个元素的特殊矩阵，故应对约束条件进行处理 .即将约束条件的左边转化成（mp+np，mnp）阶矩阵形式，约束条件的右边转化成（mnp，1）阶矩阵形式.

5）选择.传统的单纯采用赌轮选择机制的方法偶然性很大，极易导致种群的退化，故文中采用精英原则的赌轮选择机制.当一对染色体交叉时，仅当其子代的适应度大于其父代的适应度，才让子代替换父代进入种群；否则保留父代.这样不仅能有效地保持种群的最优解，又能防止种群的退化.

图1 遗传算法流程图Fig.1 Flow chart of genetic algorithm

6）交叉 .交叉步骤模仿自然界的基因重组过程 ，其作用在于将已有的优良基因遗传给下一代个体，并生成包含更复杂基因结构的新个体.即将父代按适应度值进行排序，让前半部分与后半部分分别进行交叉，并首先在两个交叉的双亲中任意选取一个交叉位置；然后，根据交叉长度确定另一个交叉位置，由此确定交叉的基因段.交叉长度取Nc＝Pc·N，其中Pc为交叉概率，N为染色体长度.

7）变异.变异的作用是为选择、交叉过程中可能丢失的某些遗传基因进行修复和补充.即随机选择个体某列，并给该列一个增量.为了较好地改进局部爬山能力，算法中采用多次变异的方法，直到本次变异的染色体序列的适应度比前一次小为止.

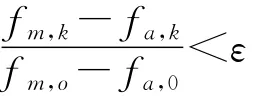
3 应用实例

采用晋江某纺织企业实际运输问题的数据，对文中提出的多种产品运输问题模型及其优化算法进行验证.该纺织企业共有3个生产车间，分别为漂染一厂、漂染二厂、漂染三厂，分别记为A1，A2，A3；生产的产品可大致划分为4大类：纯棉、涤棉、涤纶和人棉，分别记为C1，C2，C3，C4；3个车间生产的产品全部销往5个销售地，分别记为B1，B2，B3，B4，B5.表1～3分别是每天生产车间的产量数据表、销售地产品销量数据表以及单位运价表.

表1 各生产车间产量数据表Tab.1 Production data table of different manufacturing shops kg·d-1

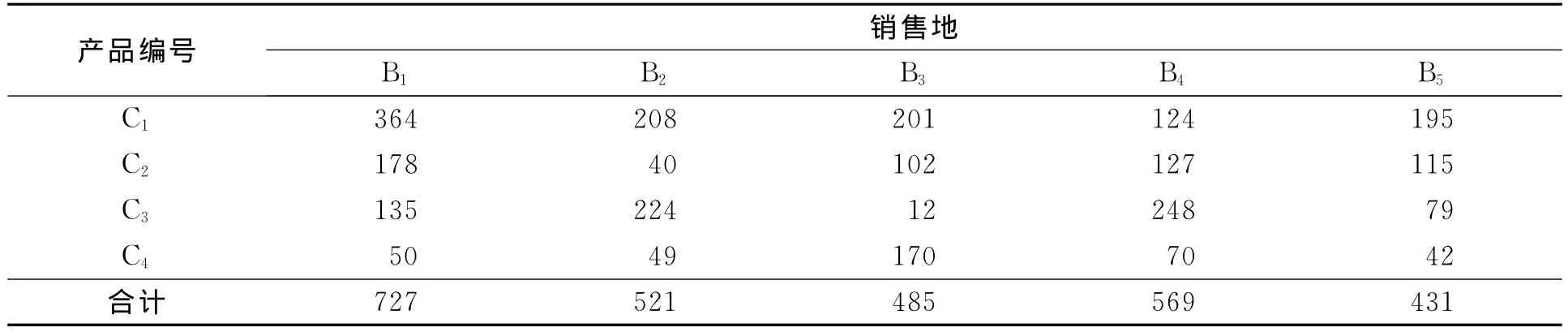
表2 销售地各产品销量数据表Tab.2 Product sales data table of sellers kg·d-1

表3 单位运价数据Tab.3 Unit price data table 元·kg-1

根据实例可知：产量和销量都是2 733kg，是一个产量等于销量的运输问题 .将以上数据代入式（1）中，可得此多产品运输问题的模型为

其单位运价矩阵C为

由式（2），（3）可知，其约束方程为

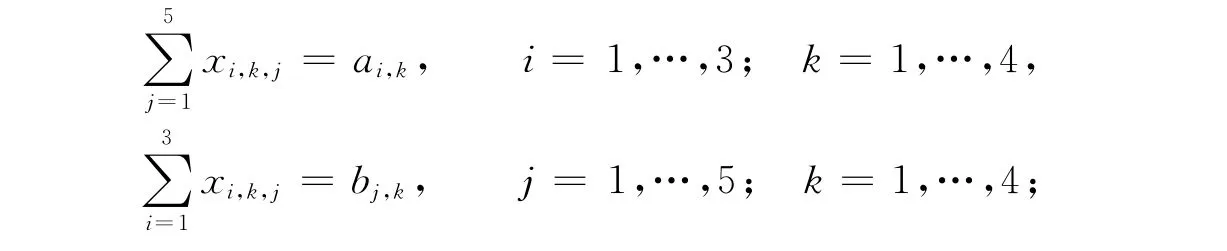
而自然约束条件为

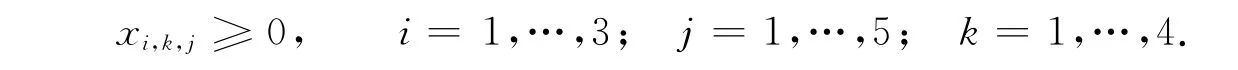
将运输模型中的单位运价系数及等式约束系数转换成矩阵形式，分别使用内点算法［8］和遗传算法进行优化，并求解该多产品运输问题，如表4所示.表4中：算法编程以Matlab 2009A为平台，运用谢菲尔德（Sheffield）遗传算法工具箱［9］；种群大小为20；最大迭代次数为100；交叉率为0.8；变异率为0.2.

表4 不同算法优化后的销售地货运量Tab.4 Sales freight volume of different optimization algorithms kg·d-1

从运行结果可以看出：使用内点算法和遗传算法时，参数exitflag皆为1，说明该函数收敛，二者运算的结果都是正确有效的 .从表4可知：对生产车间生产出的各种产品进行物资调拨，调拨出去的货运量等于产品的总生产量2 733kg，得到的最优调拨方案满足各个约束条件 .这说明该多产品的运输模型是正确的，两种求解方法都是可行的.

实例数据计算表明：内点算法与遗传算法的总运输费用分别为3 753.0，2 355.9元；总运输时间分别为18.432 2，8.182 6s.由此可知，采用遗传算法求出的运输总费用优于用内点算法计算出的结果，说明了对于大规模的多产品运输问题，采用遗传算法优化性能更好，不易陷入局部最优 .同时，遗传算法的收敛速度也优于内点算法，具有精确、快捷的特点.

4 结论

根据企业对产品运输高效低成本的需求，建立了多种产品运输问题的优化模型 .利用遗传算法解决了多种产品运输的优化求解问题，并通过实例进行验证.

研究结果表明：所建立的多种产品运输模型是与企业实际的运输问题相符合；遗传算法可快速地分析和计算出运输问题的最佳货物配送方案，不仅有效地改善了表上作业法所面对的“维数障碍”问题，也改善了内点算法在寻找最优解上的准确性，并有易于编程实现、收敛速度快等特点.

在实际生产和销售网络中，生产地和销售地都有库存，因此，进一步研究考虑库存条件下的运输问题模型及最优求解算法将更具有实际意义.

［1］ HICHCOCK F L.The distribution of a product from several sources to numerous localities［J］.J Math Phys，1941，20：224-230.

［2］ 陈宝林.最优化理论与算法［M］.北京：清华大学出版社，2009：170-176.

［3］ 蒋宏锋.运输问题一种新的表上作业法［J］.科学技术与工程，2006，24（6）：3941-3948.

［4］ 臧运华.运输问题的一种图上解法［J］.运筹与管理，2002，11（4）：81-85.

［5］ 戴庆，申静波.基于遗传算法的运输问题最优解研究［J］.天津理工大学学报，2008，24（3）：43-45.

［6］ 龚纯，王正林.精通 MATLAB最优化计算［M］.北京：电子工业出版社，2009：349-353.

［7］ 柏晖，费树岷.基于遗传算法的纺织企业机配件库存控制［J］.工业控制计算机，2011，24（11）：62-63.

［8］ 王雪.内点算法的若干基本框架及其发展［J］.泰山学院学报，2007，29（3）：13-16.

［9］ 李明.详解MATLAB在最优化计算中的应用［M］.北京：电子工业出版社，2011：382-397.