双四连杆机构运动的解析解研究

林晓哲，鲍四元

(苏州科技学院土木工程学院，江苏 苏州 215011)

0 前言

双四杆机构是机械中常用的一种机构，如文献［1］中蟑螂机器人的主要组成部分之一就是双四杆机构。另外，在啤酒装箱机、挖掘机和育苗制钵联合机中，双四杆机构以及一些类双四杆机构是其不可或缺的一部分［2－3］，但因其数学模型复杂，一直以来都是研究的难点。进行双四杆机构力学分析需要先对杆作运动学分析，如果采用理论力学中平面运动的速度、加速度基点法分析，过程繁琐。本文采用向量法对四连杆机构进行运动学分析，并给出杆件角速度、角加速度的一般表达式。

1 四连杆机构的运动学分析

四连杆机构ABCD如图1所示。

图1 四杆机构

设图1 中 AB、BC、CD 分别为1，2，3 杆，长度分别为l1，l2和l3，存在向量关系，即:

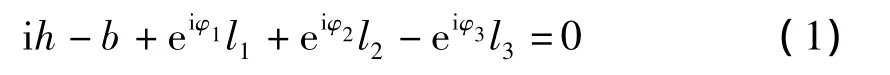
展开式(1)中复数的虚部、实部，并令其为0，得:

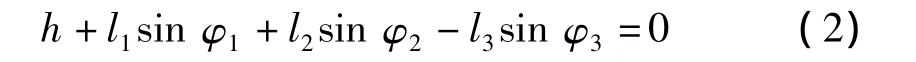
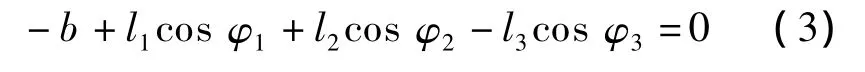
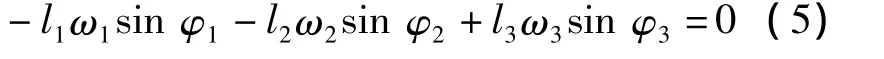
联立式(4)、式(5)，解得2、3杆的角速度:

为便于计算，式(8)可写为:

基于式(8)对式(6)、式(7)求导，并设1杆匀速转动，可得2、3杆的角加速度:

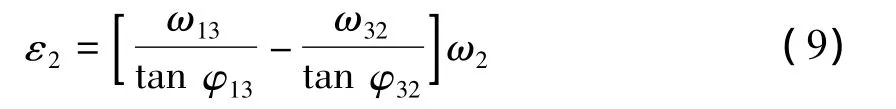
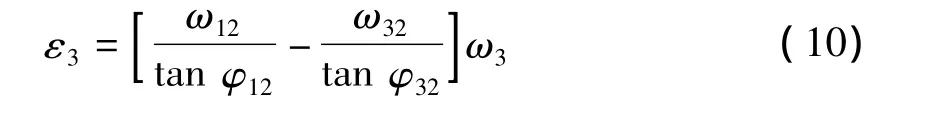
其中 φij和 ωij定义为:

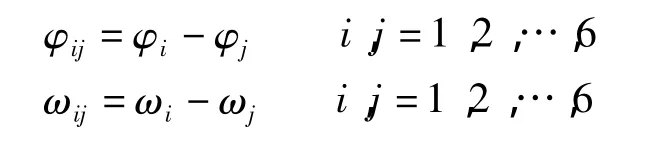
以上是四连杆机构的速度、加速度数学模型。此外，还可以得到关于角度的数学模型。当各杆长度li(i=1，2，3)已知时，解相关的三角形得到角度的数学模型如下:

其中:

2 双四连杆机构的运动学分析

双四连杆机构ABCDEFG如图2所示，设AB、BC、CD、DE、EF、FG、CE 分别为 1，2，3，4，5，6，7 杆，长度分别为，l1，l2，…，l7，设各杆长度 li(i=1，…，7)已知。图2中 A、D、G 处为铰链，铰链间竖直、水平方向的距离h、c和b、d已知。另外，△CDE中各杆夹角不变，记β=∠CDE。

图2 双四杆机构

对ABCD部分，四连杆与图1中完全相同，结论也相同，这里不再重复。对DEFG部分认为是四连杆，存在向量关系:

由于DEFG与ABCD类似，所以关于角速度的结论与式(6)、式(7)类似，只需根据杆件作相应的调整，即把所有杆件数字下标中的1、2、3相应地换成 4、5、6，且知 3、4 杆角速度相等 ω4= ω3，所以5、6杆的角速度分别为:

对式(14)、式(15)进行求导，利用式(10)可得5、6杆的角加速度分别为:

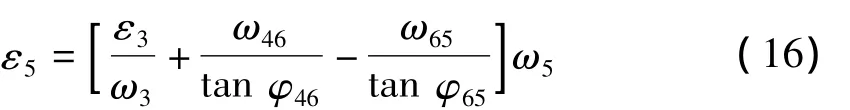
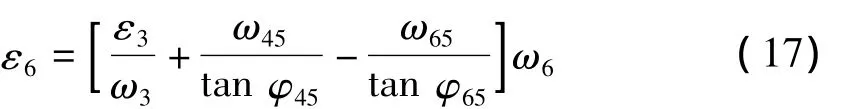
其中，ε3由式(10)确定。

设已知各杆长度和机构某状态时的1杆转角φ1，则机构的杆件角度 φ2、φ3、φBD和 lBD同式(11)、式(12)及上述相应的表达式φBD。其他角度表达式如下:

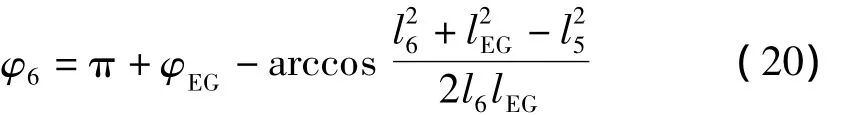
其中:

3 结论

通过向量法得到四杆机构的运动学模型，以及机构中各杆件的角速度和角加速度的解析解，并推广到双四杆机构。通过自定义角度差、角速度差的记法，所得的角速度公式形式简洁;推导角加速度时，采用函数A(t)sin F(t)/sin M(t)的导数公式，易得角加速度的表达式，简化了复杂机构的运动分析，为研究此类机构的运动分析和优化提供了一个切实可行的思路。

［1］任冠佼，陈伟海，陈斌，等．基于双四杆机构的蟑螂机器人设计与分析［J］．机械工程学报，2011，58(11):14 －22．

［2］习小英，姜莉莉，丘瑞林．双四杆机构的运动分析及其优化［J］．机械设计与制造，2010，48(1):106 －108．

［3］高玉芝，李成华．基于Pro/E的切钵机构动态仿真［J］．机械工程师，2005，36(2):45 －47．