高校二级学院综合实力评价研究
邵敏之,房汝建
(常州工学院,江苏 常州 213002)
0 引言
为了充分履行高校的社会职能,促进学科和专业发展,提高办学效能,很多本科高校都采取了二级管理模式。在二级管理模式下,二级学院是高校人才培养、科学研究、社会服务、文化创新的主阵地,是高校提高综合实力的落脚点。对二级学院综合实力进行合理评价可以较大程度地提高高校人才培养质量,促进高校可持续发展。然而,对二级学院进行客观、科学、定量化综合评价一直是高校管理实践中亟待解决的难题。
从已有的研究成果来看,对高校综合实力评价的研究,主要集中于高校校级层面综合实力的比较和分析,关于高校二级学院的研究文章相对较少,如,李中军[1]引入数据包络分析(DEA)方法客观评价校内二级学院的办学相对效益;高瞩[2]结合模糊数学分析方法,提出了高校对二级学院基层党建工作评估中的二级综合评价和评价结果分析方法;孙遒[3]结合国家对高校开展评估的实际,就本校二级学院如何贯彻“以评促建、以评促改、以评促管、评建结合、重在建设”的评估方针进行了有效探讨;戴萍萍[4]针对高校人事改革的日益深化及高校人事管理中公平合理的绩效考核方法的重要性,利用360度绩效评估方法探索科学合理的高校管理人员绩效考核方式。基于核函数的非线性主成分分析——核主成分分析(kernel Principal Component Analysis,KPCA)由 B.Scholkopf等人于1998年提出。KPCA在高维特征空间中应用主成分分析方法,能够反映数据的非线性关系,在很多领域得到成功的应用。[5-6]总体看来,对高校综合实力的研究,方法多倾向于定性分析,缺乏内在本质研究和具体性分析。
本文以常州工学院为研究对象,通过建立评价指标体系,将核主成分分析应用于常州工学院二级学院综合实力评价,并对评价结果进行了分析和说明。
1 二级学院综合实力评价指标体系
高校承担着人才培养、科学研究、社会服务和文化创新的重要职能,是实施“科教兴国”和“人才强国”战略的主要场所,这四大职能正是现代高校及二级学院的重要职能之所在,也是建立二级学院综合发展评价指标体系的重要指标。本文在高校综合实力及其影响因素分析的基础上,结合常州工学院的实际情况,构建了一套二级学院综合实力评价的新指标体系,包括21个指标考核要素,其中一级指标4个、二级指标21个,如表1所示。

表1 二级学院综合评价指标体系
2 基于核主成分分析的二级学院综合实力评价
核主成分分析在高维特征空间中运用主成分分析方法(PCA),采用非线性的方法抽取主成分,不仅适合于解决非线性特征提取问题,而且能比PCA提供更多的特征数目和更多的特征质量,可以最大限度地抽取指标的信息,因此核主成分分析在多指标评价、数据分析处理等领域得到成功而广泛的应用,已经成为重要的数据处理和分析方法。
2.1 核主成分分析
KPCA方法的基本思想是通过某种隐式方式将输入空间映射到某个高维空间(常称为特征空间),并且在特征空间中实现主成分分析(PCA),由于KPCA相较于PCA而言,引入了非线性映射,而实际数据中更多包含的是非线性关系,因此KPCA比PCA更能够准确反映现实问题中的数据关系。假设相应的映射为Φ,其定义如下:
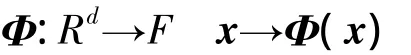
核函数通过映射Φ将隐式的实现点x到F的映射,并且由此映射而得特征空间中数据满足中心化的条件,即:

则特征空间中的协方差矩阵为:
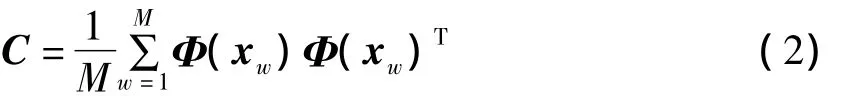
现求C的特征值λ≥0和特征向量ν:

从而有:


则有:
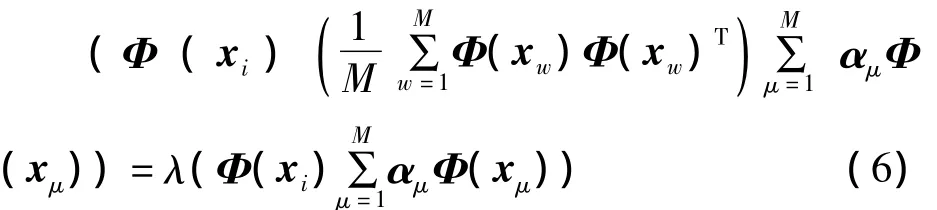
其中,i=1,2,…,M。定义M ×M 维矩阵K:

则式(6)可以简化为:

显然满足:

求解式(9)就能得到特征值和特征向量,对于测试样本在特征向量空间V的投影为:
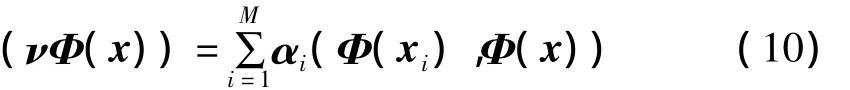
将内积用核函数替换则有:
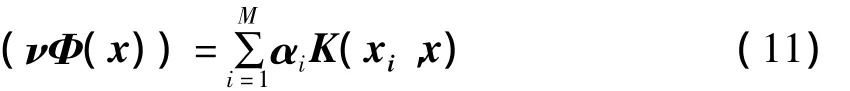
2.2 基于KPCA的综合实力评价实现步骤
基于指标体系和常州工学院11个二级学院2009—2011年度的数据,得到33×21维数据,其中33行对应3个年度11个二级学院,21列对应某年度某学院的21维二级指标数据,利用Matlab编程实现二级学院综合指标的核主成分分析以及综合实力评价分析,具体实现步骤为:
①将所获得的n个指标(每一指标有m个样品)的一批数据写成一个(m×n)维数据矩阵:
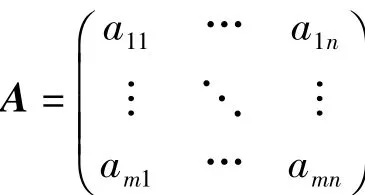
在此处 n=21,m=33。
②对矩阵A作标准化处理,即对每一个指标分量进行标准化处理。
实际过程中原始数据如果没有经过中心化,需要对数据进行标准化处理。即对每一个指标分量作标准化处理,利用Z-score法对数据进行标准化。
③计算核矩阵,先选定高斯径向核函数中的参数,再由式(7)计算核矩阵KL。
④运用Jacobi迭代方法计算KL的特征值λ1,…,λn对应的特征向量 ν1,…,νn。
⑤特征值按降序排序(通过选择排序)得λ'1,…,λ'n,并对特征向量进行相应调整,得 ν'1,…,ν'n。
⑥通过施密特正交化方法单位正交化特征向量,得到 α1,…,αn。
⑦计算特征值的累积贡献率B1,…,Bn和主成分贡献率D1,…,Dn,根据给定的提取效率p,如果 Bt≥p,则提取 t个主分量 α1,…,αt,本文取提取效率p=95%。
⑧计算已修正的核矩阵在提取出的特征向量上的投影Y=KL·α,其中α=(α1,…,αt)。所得的投影Y即为数据经KPCA降维后所得数据。
⑨选取累积贡献率达到或超过95%的t(最小整数)个主成分Y1,…,Yt,以各个主成分的贡献率Di(i=1,…,t)为权重,构造出综合评价函数为:

2.3 评价结果分析
由上述KPCA综合实力评价步骤结合3个年度11个二级学院相关数据,得到常州工学院二级学院综合实力打分及排名见表2、表3和表4。

表2 σ=30的二级学院综合实力打分及排名

表3 σ=25的二级学院综合实力打分及排名
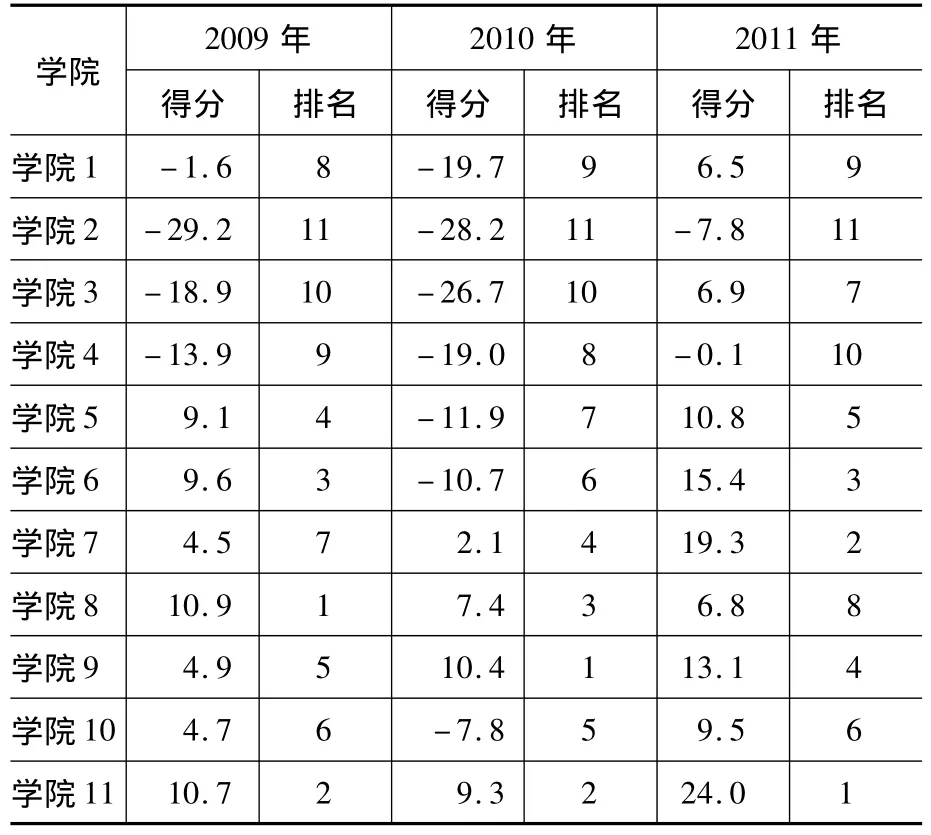
表4 σ=20的二级学院综合实力打分及排名
表2~表4给出了高斯径向基核函数3种sigma参数情况下KPCA二级学院综合实力评价。从表2~表4可以看出,使用KPCA及高斯核函数时,虽然高斯参数有所变化,但基本上能够保持综合实力打分的鲁棒性和一致性,说明KPCA打分具有一定的客观性,是真实和有效的。
3 结语
本文通过建立高校二级学院综合实力指标体系,利用核主成分分析为评价工具进行二级学院综合实力分析,客观上评价高校二级学院的办学相对效益,找出二级学院在办学过程中的不足,并据此提出解决问题的思路,从而获得更高的办学效益,同时也形成校内各二级学院相互竞争机制,督促二级学院完善专业建设和人才培养的动力和责任意识,夯实本科院校的教育教学基石,从而从根本上推动本科院校教学质量的提高、教育模式建立的成功和实现人才培养的社会认可。
[1]李中军.新升本科院校教学质量保证体系的构建与校内自我评估机制的研究[D].济南:山东师范大学,2006.
[2]高瞩.基于模糊理论的高校二级学院党建工作考核评价方法研究[J].时代人物,2007(11):87,141.
[3]孙遒.高校二级学院开展教学评估工作的思考[J].鸡西大学学报,2006,6(4):9,13.
[4]戴萍萍.360度绩效评估在高校二级学院办公室管理人员绩效考核中的应用[J].福建高教研究,2010(4):43 -45,61.
[5]向小东,宋芳.基于核主成分与加权支持向量机的福建省城镇登记失业率预测[J].系统工程理论与实践,2009,29(1):73-80.
[6]史旭明,金龙,黄小燕.基于KPCA的台风强度神经网络集合预报方法研究[J].气象科学,2013,33(2):184 -189.

