岩体结构面强度特性及地下水影响
肖桃李,艾明,路亚妮
(1.长江大学城市建设学院,湖北荆州 434023;2.武汉理工大学道路桥梁与结构工程重点实验室,湖北武汉 430070)
近10年来,随着国民经济的迅猛发展,基本建设的规模日益扩大,基础建设在向空间发展的同时,地下
资源的开发和利用也在不断走向深部.越来越多的水利、交通、军事和能源工程都不可避免地建设在含结构面的岩体地区.岩体中包含有从微观、细观到宏观缺陷的各种结构面,大量的研究及实践表明,岩体的失稳与破坏总是伴随着原生结构面的起裂、扩展和贯通,且与原生结构面的裂隙形态、分布形式及地下水因素紧密相关.结构面强度特性的研究是结构面研究领域的重要课题之一,国外Lemaitre[1]、Swoboda[2]和Kyoya[3]等学者把岩体中的结构面看作岩体自身的损伤,用损伤力学的观点、理论和方法获得岩体及结构面的力学特性;国内学者周维恒[4]、李新平[5]等学者亦从损伤断裂角度出发研究结构面岩体取得了丰硕成果;在地下水对结构面岩体影响研究方面,渗流理论与有效应力原理是研究的切入点,国外Witherspoon[6]、Louis[7]和国内朱珍德[8]、翟淑花[9]等学者在这方面进行了深入研究.近几年频发的矿难、围岩塌陷、地质滑坡等灾害性事故,大多与结构面有关,因此,对岩体结构面强度特性进行系统分析与研究具有重要的理论价值及现实指导意义.
1 岩体结构面分类
岩体结构面的分类方法众多.从工程地质学的角度而言,结构面可以划分为:原生节理、构造节理和次生节理;按地质力学观点,结构面分为:单节理、节理组、节理群、节理带和破坏带;按结构面的充填状态,可以将其划分为:平直无充填的结构面、粗糙起伏无充填的结构面、非贯通断续结构面及有充填的软弱结构面;从地质构造学的角度,结构面又可以分为:压性结构面、张性结构面、扭性结构面、压扭性结构面及张扭性结构面[10];同时,很多学者在进行结构面的实验研究中,对结构面的众多特性进行了简化,而重点探求某一特性对结构面的影响,结构面也被分为了满足研究需要的多种类型,如光滑结构面、规则齿状结构面、硬性结构面、软弱结构面等.
2 结构面的抗剪强度特性
2.1 结构面的抗剪强度
不同地质构造下的结构面实际上是凹凸不平、不规则的,不连续和起伏性是实际结构面的主要特点.
2.1.1 平直光滑无充填结构面
限于研究手段及理论落后等原因,在研究岩体结构面时,一些专家和学者把其假设为表面平整、规则,充填物单一的理想结构面.该类结构面的抗剪强度主要以结构面的微咬合和胶结作用为主,同时也与结构面表面的岩性及其平直、光滑度相关.其抗剪强度参照人工磨制面的强度计算,即

式中,τ为平直光滑无充填结构面的抗剪强度;σ为结构面的法向应力;φj,cj分别为结构面摩擦角与黏聚力.
对于光滑面的岩体结构面,日本学者吉中龙之庆和Barton等人的研究表明,湿润时的峰值抗剪强度比干燥时大且发生了剧烈的黏滑;1995年,贺建明选取泥岩和灰岩为岩样,用80#金刚砂对岩样表面进行打磨制作成光滑的结构面,研究结果则正好与日本学者的结论相反[11].
2.1.2 规则齿形结构面
1966年,Patton[12]引入结构面起伏角i来描述结构面的表面形态,并假设结构面沿齿面滑动时的黏聚力Cb为0,当法向应力较低时,Patton推导出的抗剪强度表达式为

式中,φb为齿形结构面的摩擦角;σT为齿形剪断时的临界应力值.
当法向应力较高,且超过齿形剪断时的临界应力时,外力所做的功超过剪断齿形所需的功,结构面齿形凸起部分被剪断,此时的结构面抗剪强度可表示为

式中,φ为岩体结构面表面的内摩擦角,c为岩体结构面表面的黏聚力.
在Patton等人的研究基础上,孙广忠[13]对规则齿形结构面进行了更加深入的研究,把有起伏度的结构面细分为台阶型、锯齿型和波浪型,详细研究了各种结构面的抗剪强度特性及理论推导,获得了较丰富的成果.
在规则齿形结构面抗剪性能研究方面,同济大学的沈明荣[14-15]教授进行了比较深入的研究工作,认为规则齿形结构面的抗剪强度参数与爬坡角关系密切,并通过模型实验方法验证了随着爬坡角增加,结构面抗剪强度参数亦逐渐增大.同时,文献[14-15]采用规则齿形结构面的水泥砂浆试件,在不同应力状态下进行常规剪切实验和卸载剪切实验研究,总结出规则齿形结构面的抗剪强度公式:
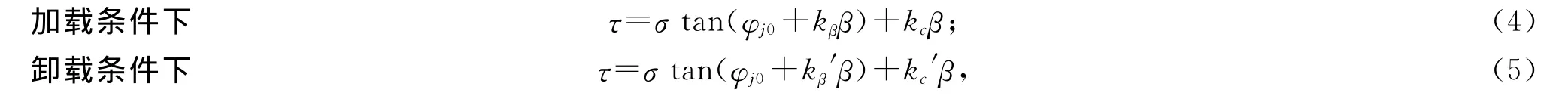
式中,β为结构面的爬坡角;φj0为结构面的基本内摩擦角;kβ,kβ′分别为加载和卸载时结构面的综合内摩擦角修正系数;kc,kc′分别为加载和卸载时结构面的综合黏聚力修正系数.
2.1.3 不规则起伏结构面
与理想中的规则齿形结构面相反,工程岩体中绝大部分结构面的起伏形态是不规则的,不仅起伏角度和高度不易量测,而且起伏形态也无规律性,该种结构面的特点以随机而离散分布为主.
Ladanyi和Archambault[16]自1970年开始,通过在岩体中人工制作大量的粗糙结构面开展剪切实验,对结构面从剪胀到剪断全过程进行了全面分析与研究,获得了如下的抗剪强度公式:

式中,αs为结构面剪断率,指被剪断的凸起部分的面积与整个剪切面积的比值;n为剪胀率,指剪切时的垂直位移与水平位移的比值;τr为凸起体岩石的抗剪强度;φu为结构面的基本摩擦角.
Barton[17]对8种不同粗糙起伏的结构面进行了实验研究,提出了剪胀角的概念,并用以代替起伏角,剪胀角定义为剪切时剪切位移的轨迹线与水平线的夹角.Barton通过对大量的实验资料的统计发现,结构面的峰值剪胀角不仅与凸起高度有关,而且与作用于结构面的方向应力σ、结构面的抗剪强度τ及壁岩强度JCS之间也存在良好的统计关系,在此基础上,Barton推导出结构面抗剪强度公式

式中,JRC表示粗糙度系数;JCS表示结构面抗压强度;φu为结构面的基本摩擦角.
张林洪[18]通过对岩体进行回弹实验,使用摄影测量方法进行结构面粗糙度测量,建立了一套用回弹试验、摄影测量及由实验结果建立的公式确定结构面抗剪强度的方法:
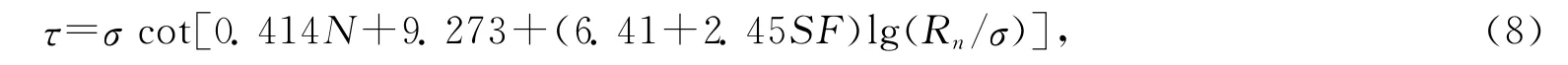
式中,N为结构面面壁上的回弹值;SF为面壁的形貌参数;Rn为结构面面壁单轴抗压强度平均值.
2008年,童志怡,陈从新等[19]尝试引入摩擦学中的黏着磨擦理论对结构面的摩擦过程进行分析,根据结构面剪切过程中实际接触面积的变化规律,建立了结构面抗剪强度选取的新方法:

式中,Ar为直剪过程中结构面的实际接触面积;s为实际剪切位移量.
2.2 结构面的强度准则
大量研究表明,均质岩体内岩体破坏面与主应力面总是成一定的角度关系.当剪切受力时,破裂面总是与大主应力面法线方向成α=45°+φ/2夹角;当受拉伸应力时,破裂面就是主应力面.而一旦岩体中存在软弱结构面,剪切受力时,其破裂面可能是α=45°+φ/2的面,但绝大多数情况下,破裂面就是软弱结构面,即破裂面与主应力的夹角就是软弱结构面与主应力的夹角.
图1为含结构面岩体受力图,σ1、σ3为岩体所处的应力状态,结构面方向与σ1面的夹角为β.根据该处岩体的应力状态绘制的应力圆和强度包络线如图2所示,图2中CD为岩体的强度包络线(c和φ分别为岩体的黏聚力和内摩擦角),AB为软弱结构面的强度包络线(cj和φj分别为结构面的黏聚力和内摩擦角),M点为软弱结构面的应力状态点,根据莫尔-库伦准则,如果M点位于AB之间,说明岩体结构面剪切应力大于结构面的抗剪强度,结构面以滑动破坏为主;如果M位于AB下方,说明岩体结构面的剪应力小于结构面的抗剪强度,结构面是稳定的.因此,岩体是否沿结构面滑动破坏的判定条件与角度β1和β2相关.
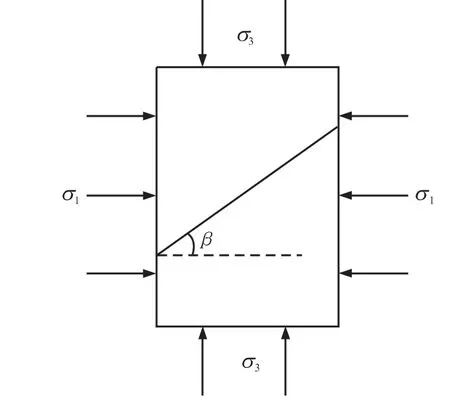
图1 受力的岩体单元Fig.1 Rockmass unit under loads

图2 结构面的应力状态Fig.2 Stress condition of structural surface

式(10),(11)给出了角度β1和β2的计算式,如前分析,当结构面倾角β1<β<β2,岩体破坏特征为沿结构面的剪切破坏;当β<β1或β<β2时,则岩体的破坏特征与结构面的存在无关,属于岩体自身的剪切破坏;当β等于β1或β2,岩体的破坏介于沿结构面破坏或岩体自身破坏的临界状态.
3 地下水对结构面强度的影响
水对岩体的影响主要包括2个方面:一是水对岩石的软化作用,水的存在使得岩体的力学性能降低,黏聚力和内摩擦角减小;二是水与岩体相互耦合作用下的力学效应,一旦饱和岩石在荷载作用下不易排水或不能排水,则岩体孔隙或裂隙中产生孔隙水压力(图3),相应的岩石颗粒所承受的压力减小,强度降低.根据莫尔-库仑准则,则有

图3 理想结构面饱水受力Fig.3 Stress condition of saturated ideal structural surface
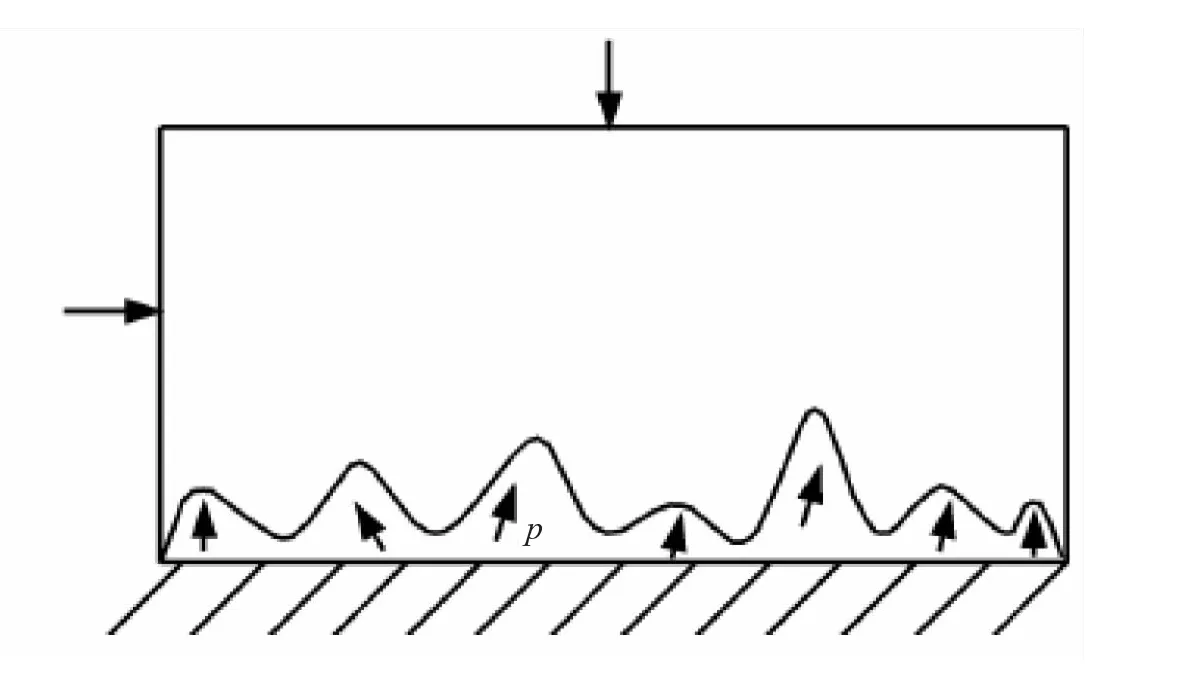
图4 含水结构面与岩体接触关系Fig.4 Contact retation between rockmass and structural surface of water-bearing

式中,τn为岩体的抗剪强度;c为岩体的凝聚力;φ为岩体的内摩擦角;σ为结构面上覆岩体作用在结构面上的正应力;p为结构面上的孔隙水压力;σe为作用在结构面上的有效应力.
式(3)表明,岩体中结构面由于孔隙水的存在,使有结构面受到的有效应力σe降低,岩体产生剪切破坏的极限应力τn也降低,因此,岩体沿结构面的剪切滑动破坏更容易发生.
图3为理想结构面的饱水受力状态,结构面上下岩体为光滑面,但自然界中的岩体结构面往往是随机而无规律可循的,因此,结构面中孔隙水压的作用仅产生于接触面孔洞部位(图4).事实上,结构面与岩壁的接触面由于孔隙水压力和裂隙水化的双重作用,其力学性质与理想的塑性变形相当[14],因此

式中,A0为结构面上、下表面岩体的实际接触面积;σ0为岩体塑性屈服应力;W为结构面上覆岩体的重量;p为结构面内孔隙水压力;A为结构面表面积.变换(13)可得

假设结构面与岩体之间的有效接触为弹性接触,其有效接触面积为A0,则作用在结构面上的有效应力σe为

令λ=A0/A,则

将式(16)代入式(12),得

式(17)即为考虑岩体结构面中孔隙水压和水化双重作用影响后的岩体破坏的莫尔-库仑破裂准则.假设结构面与岩体的夹角为θ,则倾斜结构面在自重应力作用下滑动的临界角满足方程

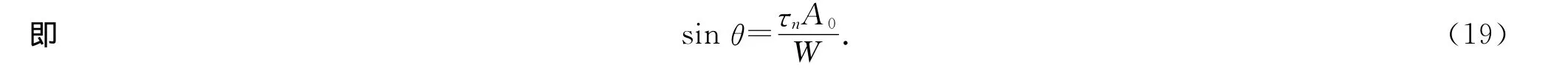
将式(17)代入式(19),得
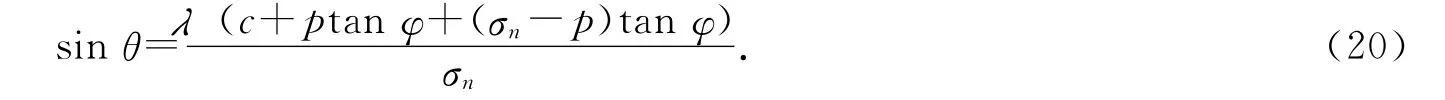
上式可以看出,λ越小,表明结构面与岩体的有效接触面积A0越小,则θ越小,说明岩体滑动所需的临界角就越小;对于孔隙水压力p而言,有效应力减小,则有效接触面积A0减小,因此当结构面中存在孔隙水压力时,结构面与岩体的夹角即使较小,也较容易发生剪切滑动破坏.因此,工程岩体中赋存的地下水能加速岩体沿结构面的剪切滑移破坏.
4 结论
通过对岩体结构面强度理论的分析与总结,可以得出以下结论:1)压应力状态下的节理岩体的破坏分为2种情况,一种是岩体沿着结构面的剪切滑移破坏,另一种是岩体自身的剪切破坏,岩体的破坏形式判断可以用结构面的倾角表示,当β1<β<β2时,岩体沿结构面剪切破坏,当β<β1或β>β2时,则岩体的破坏是岩石的剪切破坏;2)岩体结构面内充填的地下水能够承担及传递压力,因此地下水对岩体结构面强度具有弱化作用;当岩体沿结构面剪切破坏时,地下水的作用能加速剪切破坏的发生.
[1] LEMAITRE J.How to use damage mechanics[J].Nuclear Engineering and Design.1984,80:233-245.
[2] SWOBODA H,YANG Q.Damage propagation model and its application to rock engineering problem[A].In:Int Cong Rock mechanics proceeding[C].Tokyo:[s.n.],1995:159-163.
[3] KAWAMOTO T,ICHILAWA Y,KYOYA T.Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory[J].Int J Num Analy Geo,1998,12:1-30.
[4] 周维恒,杨若琼,吴澎.节理岩体的损伤力学模型[M].中国岩石力学与工程学会教育工作委员会.岩石力学新进展.沈阳:东北工学院出版社,1989.
[5] 李新平,朱维申.多裂隙岩体的损伤断裂分析与工程应用[J].岩体工程学报,1992,14(4):1-7.LI Xinping,ZHU Weishen.The damage-fracture analysis of jointed rock mass and its application in engineering[J].Chinese Journal of Geotechnical Engineering,1992,14(4):1-7.
[6] WITHERSPOON A.New approaches of fluid flow in fractured rock masses[J].Proc US Symp Rock Mech,1981,22:1-20.
[7] WALSH C B.Effect of pore pressure and confining pressure on fracture permeability[J].Int J Rock Mech and Min Sci,1981,18:429-435.
[8] 朱珍德,郭海庆.裂隙岩体水力学基础[M].北京:科学出版社,2007.
[9] 翟淑花,李文秀,高谦,等.基于遗传规划的岩石流变模型辨识[J].河北大学学报:自然科学版,2008,28(6):578-582.ZHAI Shuhua,LI Wenxiu,GAO Qian,et al.Identification of rheological constitutive model of rock based on genetic programming[J].Journal of Hebei University:Natural Science Edition,2008,28(6):578-582.
[10] 韩丛发.煤矿生产中常见的结构面及其力学性质鉴定[J].煤炭技术,2003,22(7):91-92.HAN Congfa.The familiar parting plane in mine production and the determination of its mechanic property[J].Coal Technology,2003,22(7):91-92.
[11] 贺建民.对光滑结构面所具特性的一些新认识[J].力学与实践,1995,17(2):30-32.HE Jianmin.Some new understanding about the smooth structure surface features[J].Mechanics in Engineering,1995,17(2):30-32.
[12] PATTON F D.Multiple modes of shear failure in rock[Z].The Ist Congress of International Society of Rak Mechanics,Lisbon,1966.
[13] 孙广忠.岩体结构力学[M].北京:科学出版社,1988.
[14] 张清照,沈明荣,张龙波.结构面在卸载条件下的力学研究[J].地下空间与工程学报,2009,5(6):1126-1130.ZHANG Qingzhao,SHEN Mingrong,ZHANG Longbo.Study on the mechanical properties of rock discontinuity under unloading[J].Chinese Journal of underground Space and Engineering,2009(6):1126-1130.
[15] 沈明荣,张清照.岩体结构面的剪切试验研究[J].地下空间与工程学报,2010,6(1):38-43.SHEN Mingrong,ZHANG Qingzhao.Study on shearing test of rock mass discontinuity[J].Chinese Journal of Underground Space and Engineering,2010,6(1):38-43.
[16] LADANYI B,ARCHAMBULT G.Simulation of shear behavior of ajointed rock mass[C]//SOMERTON W H.Proc 11th Symp on Rock Mechanics.[s.l.]:1970:105-125.
[17] BARTON N R.The shear strength of rock and rock joints[J].Int J Rock Mech Min Sci&Geomech Abstr,1976,13:255-279.
[18] 张林洪.结构面抗剪强度的一种确定方法[J].岩石力学与工程学报,2001,20(1):114-117.ZHANG Linhong.A determination method of joint shear strength[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(1):114-117.
[19] 温诗铸,黄平.摩擦学原理[M].2版.北京:清华大学出版社,2002.
[20] 童志怡,陈从新,徐健,等.基于黏着摩擦理论的结构面抗剪强度选取方法[J].岩土工程学报,2008,30(9):1367-1371.TONG Zhiyi,CHEN Congxin,XU Jian,et al.Selection of shear strength of structural plane based on adhesion friction theory[J].Chinese Journal of Geotechnical Engineering,2008,30(9):1367-1371.

