一种简单有效的人脸识别方法
翟俊海,赵文秀,2,李塔
(1.河北大学数学与计算机学院,河北省机器学习与计算智能重点实验室,河北保定071002;2.中国气象局气象干部培训学院河北分院教务科,河北保定071000)
人脸识别也称自动人脸识别,是一个近年得到广泛关注的研究热点[1].人脸识别的方法大致可分为2类:基于外观的方法和基于特征的方法.基于外观的方法将待识别的对象看作图像空间中的一个点,利用统计方法得到其分布,然后利用该分布进行人脸识别.在协方差矩阵、特征值和特征向量概念的基础上,Turk等人[2]提出了著名的特征脸方法,也称为主成分分析(PCA)方法.PCA方法没有考虑类别属性对识别的贡献,针对这一问题,Belhumeur等人[3]提出了费舍尔脸方法,也称为线性判别分析(LDA)方法.PCA方法和LDA方法都需要对图像数据向量化,而向量化后的数据维数非常高,会出现小样本问题.另外,求高阶协方差矩阵的特征值和特征向量非常耗费时间.Yang等人[4]提出的2DPCA和Li等人[5]提出的2DLDA可以有效解决上述问题.2DPCA和2DLDA直接从图像数据构造图像协方差矩阵和图像散度矩阵,不需要向量化的过程,这样降低了PCA和LDA的计算时间复杂度.但2DPCA和2DLDA对原图像只沿水平方向进行投影,与PCA和LDA相比,需要更多的存储空间,为克服这一缺点,ZHANG等人[6]提出了双向二维主成分分析((2D)2PCA)方法,Noushanth等人[7]提出了双向二维线性判别分析((2D)2LDA)方法.杨万扣等人[8]提出了基于对称二维主成分分析的人脸识别方法.王科俊等人[9]提出了基于子模式的完全二维主成分分析方法.基于特征的方法主要利用人脸图像的几何特征(如眼睛、眉毛、鼻子等)以及它们之间的几何关系进行人脸识别[1].Wiskptt等人[10]提出的图匹配方法和Samaria等人[11]提出的隐马尔科夫模型(HMM)方法是这类方法的杰出代表.目前,基于外观的人脸识别方法是研究的热点.
在基于外观的方法中,近几年研究人员提出了许多基于小波变换的方法,如Lai等人[12]将小波变换和傅里叶变换结合起来,提出的人脸识别方法可以很好地解决不变性问题.而Dai等人[13]将小波变换与线性判别分析结合起来,提出的人脸识别方法可以解决小样本问题.另外,Kwak等人[14]提出了基于小波变换和模糊积分相结合的人脸识别方法.邹建法等人[15]提出了基于增强Gabor特征和直接分步线性判别分析的人脸识别方法.Ergun等人[16]对基于小波变换和PCA的人脸识别方法进行了分析比较.Mohammed等人[17]提出了基于小波变换和极端学习机的人脸识别方法,该方法分为3步,首先对人脸图像做小波变换,然后用双向二维主成分分析进行特征提取,最后用极端学习机进行分类识别.但实验研究发现,用小波变换的低频子图直接作为极端学习机的输入,就可以达到非常好的识别效果,换句话说,第2步的特征提取是没有必要的.在3个人脸数据库上与Mohammed等人[17]提出的方法进行了实验比较,实验结果显示与文献[17]中的方法相比,本文提出的方法更简单有效.
1 小波变换
在此简要介绍将要用到的小波变换[18]的基础知识.
设f(x,y)是一幅人脸图像,f(x,y)的小波变换如图1所示.包括沿水平方向和垂直方向的滤波及降2采样.沿水平方向的低通滤波是通过滤波器L实现的,而高通滤波是通过滤波器H实现的.沿垂直方向的滤波和沿水平方向的滤波类似.
图1中,fLL表示沿水平和垂直2个方向的低频成分;fLH表示水平方向的低频成分和垂直方向的高频成分;fHL表示水平方向的高频成分和垂直方向的低频成分;fHH表示沿水平和垂直2个方向的高频成分.人脸图像的识别信息主要包含在低频子图中,高频子图包含的是人脸图像的边界轮廓信息.对一层小波分解得到的低频子图重复进行小波变换可得二层小波变换.重复此过程得到多层小波变换,因为小波变换具有降2采样的特性,所以一幅图像经过几层小波变换后,低频子图维数就会变得很小.如256×256的图像,经5层小波变换后,低频子图变为大小为8×8的图像.
2 基于小波变换和极端学习机的人脸识别方法
极端学习机(ELM:Extreme Learning Machine)是Huang等人[19]提出的用于训练单隐含层前馈神经网络(图2)的学习算法.ELM算法要求该网络的隐含层激活函数是Sigmoidal函数,输入层和输出层激活函数为线性函数.ELM不需要迭代调整权参数,而是随机地产生输入层到隐含层的权值和隐含层结点的偏置,然后用分析的方法确定隐含层到输出层的权值,具有学习速度快、泛化能力强等特点.
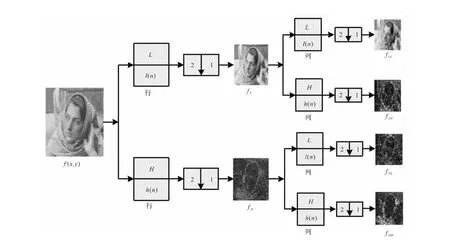
图1 图像的小波变换示意Fig.1 Flowchart of image wavelet transforms
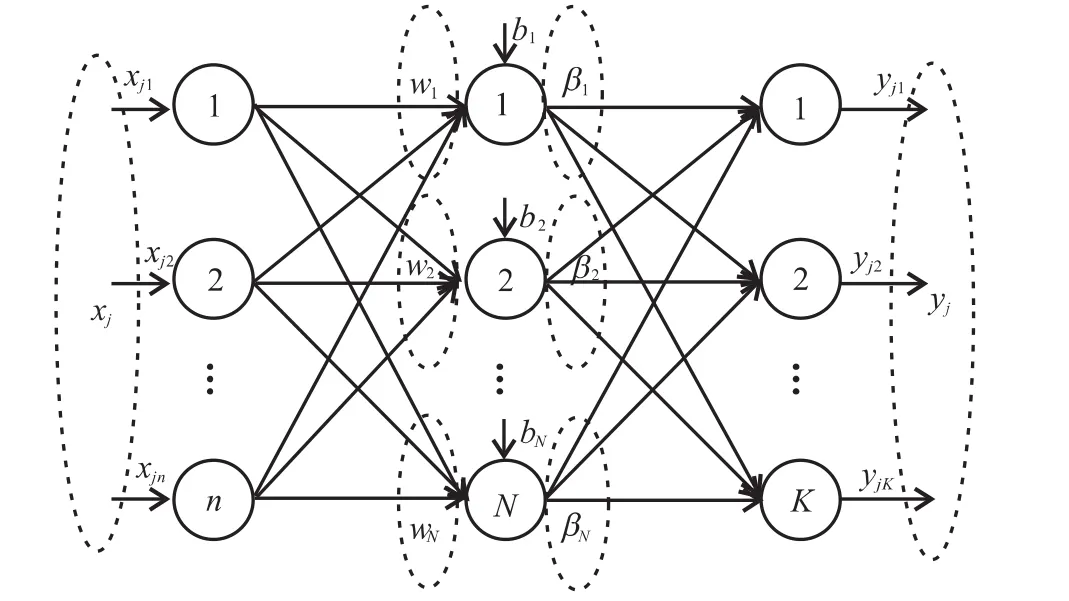
图2 单隐含层前馈神经网络Fig.2 Single-hidden layer feed-forward neural networks
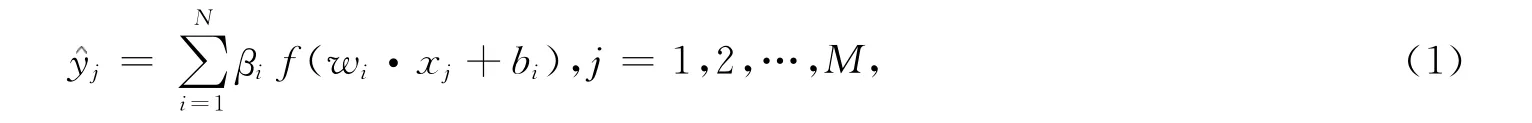
其中,wi=(w1i,w2i,…,wni),βi=(βi1,βi2,…,βiK),i=1,2,…,N,(1)式的矩阵表示为Hβ=Y,其中,
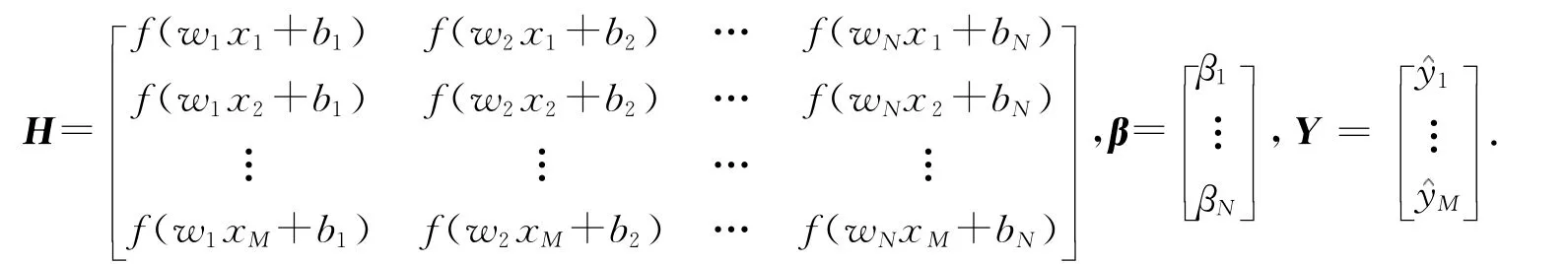
ELM算法描述如下.
输入:训练集D=,j=1,2,…,M},隐含层结点个数N和隐含层激活函数g(x);
输出:隐含层权矩阵β.
算法步骤
Step1.随机指定输入层权值wi和隐含层偏置bi(i=1,2,…,N);
Step2.计算隐含层输出矩阵H;
Step3.计算输出层权矩阵β=H+T,其中H+是H的广义逆矩阵.
ELM在应用中取得了非常好的效果,即ELM具有非常好的泛化能力,但其理论依据尚不清楚,目前依然是ELM研究领域的公开问题.从ELM的实验研究可得出结论[20]:对于分类问题,当ELM网络的隐含层结点个数达到一定值时(一般情况下,这个值都高于输入层结点个数,即输入层到隐含层的映射是一个升维映射),分类测试精度都能达到非常理想的结果.对于基于小波变换和ELM的人脸识别,实验研究发现,用文献[20]中的方法确定隐含层结点个数后,把人脸图像经小波变换后的低频子图直接作为ELM网络的输入,就能得到非常好的识别效果,而不需要像文献[17]中那样,再从小波子图中用投影子空间方法(如双向二维主成分分析)进行特征提取.与文献[17]中的方法相比,本文方法的分类识别精度(测试精度)和文献[17]中方法的识别精度相当,但所用CPU时间要少很多.本文方法分为训练和测试2步.
训练算法
输入:人脸数据库,小波变换的层数L,隐含层结点个数N和隐含层激活函数g(x);
输出:隐含层输出矩阵
Step1.对人脸数据库中的每一幅人脸图像做L层小波变换,得到第L层的小波低频子图;
Step2.随机指定输入层权值wi和隐含层偏置bi(i=1,2,…,N);
Step3.输入训练集中向量化后的小波低频子图,计算隐含层输出矩阵H;
Step4.计算输出层权矩阵β=H+T,其中H+是H的广义逆矩阵.
Step5.得到训练好的ELM网络.
测试算法
Step1.对每一幅测试人脸图像,做L层小波变换,得到第L层的小波低频子图;Step2.向量化小波低频子图,并输入训练好的ELM网络,计算其对应的输出值;Step3.根据输出值,确定其类别.
3 实验结果
用ORL,JAFFE和FERET 3个人脸数据库与文献[17]中的方法进行了实验比较.ORL人脸数据库中包括40个人的人脸图像.这些人脸图像是在不同的时间、不同光照、不同的表情等条件下拍摄的.JAFFE人脸数据库中包括10个人的213幅不同表情的图像.FERET人脸数据库中包括20个人的641幅不同姿势的图像.实验环境是PC机,双核1.86GCPU,2G内存,Windows XP操作系统,Matlab 7.1实验平台.
实验1 小波基函数的选择
人脸图像的小波变换本质上是将人脸图像(函数)表示为一系列不同尺度的小波基函数的叠加,小波变换的性能与小波基函数的性质紧密相关,这些性质包括对称性、正交性、紧支撑、消失矩,理论上已经证明了同时满足这些性质的小波基函数是不存在的.实际应用中一般要求小波基函数具有正交性或双正交性,这样可使冗余达到最小.笔者实验研究了选用不同的正交小波和双正交小波对识别精度的影响.对于正交小波,实验比较了dbN(N=1,2,…,10),symN(N=2,3,…,8)和coifN(N=1,2,…,5)小波族选不同的N(即选不同的正交小波)对识别精度的影响.对于双正交小波,实验比较了biorNr.Nd(Nr.Nd=1.1,1.3,1.5;2.2,2.4,2.6,2.8;3.1,3.3,3.5,3.7,3.9;4.4;5.5;6.8)和rbioNr.Nd(Nr.Nd=1.1,1.3,1.5;2.2,2.4,2.6,2.8;3.1,3.3,3.5,3.7,3.9;4.4;5.5;6.8)双正交小波族选不同的Nr.Nd(即选不同的双正交小波)对识别精度的影响.为了获得不同的小波在不同的数据集上最优的N或Nr.Nd,首先通过具有不同的N或Nr.Nd的每类小波对每个数据集进行了小波变换,选低频子图构造数据集,然后使用十折交叉验证法得到了ELM网络在每个子集上的测试精度.图3a-e是在ORL数据库上的实验结果,由于篇幅所限,在其他2个数据库上的实验结果没有列出,结果是类似的.
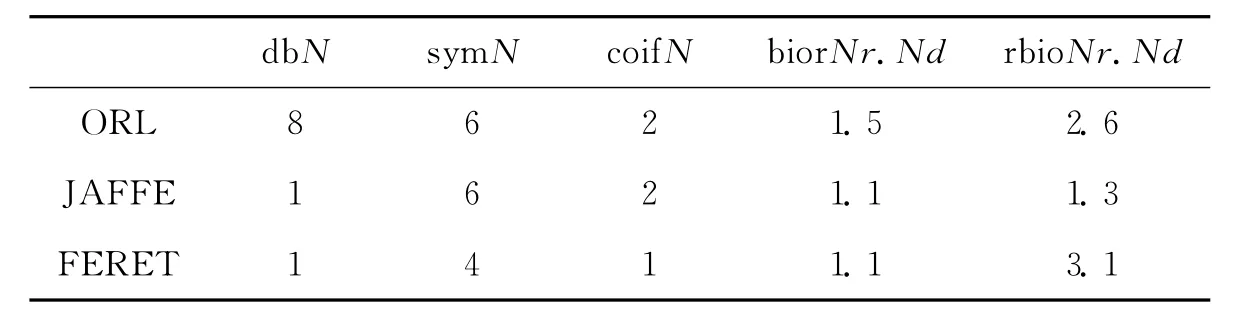
表1 在不同人脸数据库上的最优小波基函数Tab.1 Optimal wavelet basic functions in different face databases
实验2 与文献[17]中方法的性能比较
根据上表确定的最优小波基函数,对3个人脸数据库进行了不同层次的小波变换.其中维数较小的ORL变换到第5层,而维数较大的JAFFE和FERET数据集变换到第6层.然后用低频子图直接作为ELM网络的输入进行人脸识别,与文献[17]中的方法从测试精度和所用的CPU时间2个方面进行了比较,在3个人脸数据库的实验比较结果列于表2.表2的实验结果可看出,测试精度和文献[17]中方法的测试精度大体相同,但所用的CPU时间本文方法要少得多.主要原因:1)是ELM不需要迭代调整输入层权值和隐含层偏置,而是随机指定这些参数,然后用分析的方法确定输出层的权值.ELM的学习速度非常快,而且具有非常好的泛化能力;2)是本文方法是两阶段方法,而文献[17]中的方法是三阶段方法.本文方法小波变换后不用计算低频子图的双向主成分,直接输入到ELM网络进行分类识别,因为求双向二维主成分的过程实际上是求图像协方差矩阵的特征值和特征向量的过程,而计算矩阵的特征值和特征向量非常耗费时间,所以本文方法所用的CPU时间要比文献[17]中的方法少很多.实验结果显示,与文献[17]中的方法相比,本文提出的方法更简单有效.
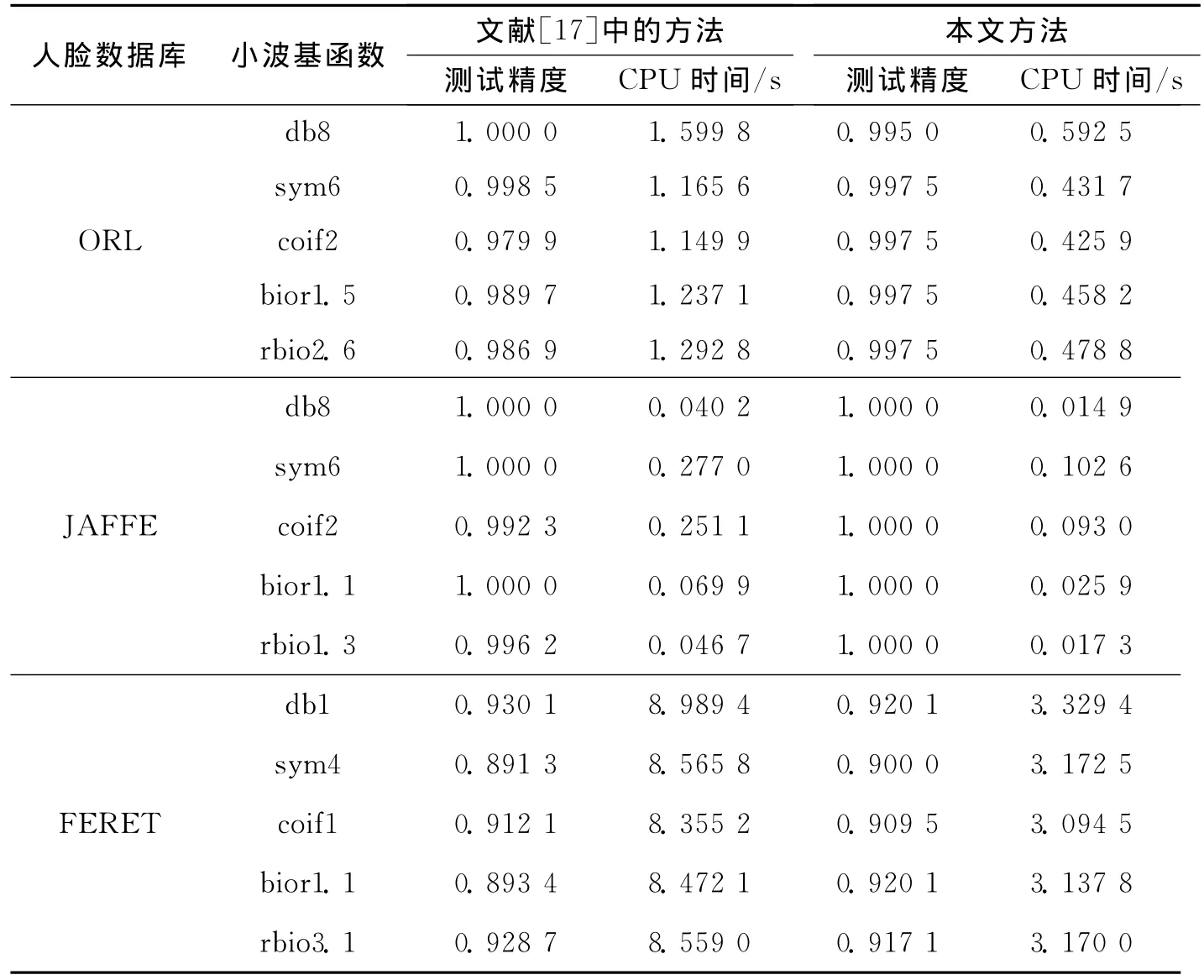
表2 本文方法与文献[17]中方法实验比较的结果Tab.2 Comparative results between the proposed method and the one in[17]
4 结论
文献[17]中的人脸识别方法对人脸图像做小波变换后,再用双向二维主成分分析进行特征提取,最后用ELM网络进行分类识别.实验研究发现,人脸图像做小波变换后的低频子图直接作为ELM网络的输入,而不用进行双向二维主成分分析进行特征提取,依然可以得到非常好的分类识别效果,而且所用的CPU时间可以大幅度地降低.实验研究了小波基函数的选择对分类识别精度的影响,并与文献[17]中的方法从测试精度和所用的CPU时间两方面进行了实验比较,实验结果显示,与文献[17]中的方法相比,本文提出的方法更简单有效.另外,对于不同的人脸数据库得到了最优的小波基函数,可为相关研究提供实验参考.
[1] 章毓晋,贾彗星,李乐,等.基于子空间的人脸识别方法[M].北京:清华大学出版社,2009.
[2] TURK M,PENTLAND A.Eigen-faces for recognition[J].Journal of cognitive neuroscience,1991,3(1):71-86.
[3] BELHUMEUR P N,HESPANHA J P,KRIEGMAN D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.
[4] YANG Jian,ZHANG David.Two-dimensional PCA:A new approach to appearance-based face representation and recognition[J].IEEE Transactions Pattern Analysis and Machine Intelligence,2004,26(1):131-137.
[5] LI Ming,YUAN Baozong.2D-LDA:A novel statistical linear discriminant analysis for image matrix[J].Pattern Recognition Letter,2005,26(5):527-532.
[6] ZHANG Daoqiang,ZHOU Zhihua.(2D)2PCA:Two-directional two-dimensional PCA for efficient face representation and recognition[J].Neurocomputing,2005,69(1-3):224-231.
[7] NOUSHATH S,KUMAR G H,SHIVAKUMAR P.(2D)2LDA:An efficient approach for face recognition[J].Pattern Recognition,2006,39(7):1396-1400.
[8] 杨万扣,任明武,杨静宇.基于对称二维主成分分析的人脸识别[J].模式识别与人工智能,2008,21(3):326-331.YANG Wankou,REN Mingwu,YANG Jingyu.Face recognition based on symmetrical 2DPCA[J].Pattern Recognition and Artificial Intelligence,2008,21(3):326-331.
[9] 王科俊,贲晛烨,刘丽丽,等.基于子模式的完全二维主成分分析的步态识别算法[J].模式识别与人工智能,2009,
22(6):854-861.
WANG Kejun,BEN Xianye,LIU Lili,et al.Subpattern-based complete two dimensional principal component analysis for gait recognition[J].Pattern Recognition and Artificial Intelligence,2009,22(6):854-861.
[10] WISKPTT L,FELLOUS J M,MALSBURG C V.Face recognition by elastic bunch graph matching[J].Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):775-779.
[11] SAMARIA F,YOUNG S.HMM based architecture for face identification[J].Image Vision Computing,1994,12(8):537-583.
[12] LAI Jianhuang,YUEN P C,FENG Guocan.Face recognition using holistic Fourier invariant features[J].Pattern Recognition,2001,34(1):95-109.
[13] DAI Daoqing,YUEN P C.Wavelet based discriminant analysis for face recognition[J].Applied Mathematics and Computation,2006,175(1):307-318.
[14] KWAK K C,PEDRYCZ W.Face recognition using fuzzy integral and wavelet decomposition method[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B,2004,34(4):1666-1675.
[15] 邹建法,王国胤,龚勋.基于增强Gabor特征和直接分步线性判别分析的人脸识别[J].模式识别与人工智能,2010,23(4):477-482.ZOU Jianfa,WANG Guoyin,GONG Xun.Face recognition based on enhanced gabor feature and direct fractional-step linear discriminant analysis[J].Pattern Recognition and Artificial Intelligence,2010,23(4):477-482.
[16] ERGUN G,NIYAZI K,AHMET S,et al.Evaluation of face recognition techniques using PCA,wavelets and SVM[J].Expert Systems with Applications,2010,37(9):6404-6408.
[17] MOHAMMED A A,MINHAS R,WU Q M J,et al.Human face recognition based on multidimensional PCA and extreme learning machine[J].Pattern Recognition,2011,44(10-11):2588-2597.
[18] MALLAT S G.A theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(1):674-693.
[19] HUANG Guangbin,ZHU Qinyu,SIEW C K.Extreme learning machine:theory and applications[J].Neurocomputing,2006,70(1-3):489-501.
[20] 翟俊海,李塔,翟梦尧,等.ELM中随机映射作用的实验研究[J].计算机工程,2012,38(20):164-168.ZHAI Junhai,LI Ta,ZHAI Mengyao,et al.Experimental research on random mapping functions in ELM[J].Computer Engineering,2012,38(20):164-168.

