基于集合经验模态分解和支持向量机的短期风速预测模型

祝晓燕，张金会，付士鹏，朱霄珣

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

0 引言

随着国家对风力等的新能源大力支持，风力开发正在迅猛的发展。然而，风能的不稳定性造成了发电质量的下降，严重制约着风力发电的发展。为了提高发电质量，减少风能对电网的冲击，同时也为了减少风电场的运行成本，就必须了解风速的变化规律，及时、准确的对风速进行预测，才能帮助调度部门及时的调整计划，实现安全并网。

所谓风速的短期预测是指预测以分或小时为单位进行短期的阶段预测。对短期风速的直接预测，其精度有限，但随着风电的迅猛发展，预测方法的不断创新、丰富，预测精度有了大幅度的提高，误差在逐渐的减小。

本文根据风电场获得地现场数据，建立了一种基于集合模态分解(Ensemble Empirical Mode Decomposition，EEMD)和粒子群算法(Particle Swarm Optimization，PSO)优化支持向量机(Sup-port Vector Machine，SVM)的预测模型。并通过与SVM直接预测方法进行了精度比较，验证了本文方法的优越性。

1 理论基础

1.1 EEMD算法原理

EEMD是在EMD方法的基础上的改进，其原理为通过在EMD分解过程中加入高斯白噪声的方法来解决EMD的模态混叠的现象。

1.1.1 EMD算法原理

经验模态分解(Empirical Mode Decomposition，EMD)是一种高效的信号分解方法[1，2]。他具有很好的自适应性，非常适用于非线性、非平稳的信号的处理。它基于信号的局部特征尺度，将任意信号中不同尺度的波形或趋势逐级分解出来，产生一系列相对平稳并具有不同特征尺度的本征模态函数(Intrinsic Mode Function，imf)。

EMD的分解过程为:将任意的信号x(t)的上包络线和下包络线所对应的点取平均，得到一条平均线h，然后再求信号x(t)与平均线h的差值m;然后把m作为新的原始信号在重复之前的过程，得到imf1;将x(t)除去imf1再进行上表面的过程得到imf2;重复上面的过程，依次得到imf2，imf3…imfn和残余分量r(代表信号的平均趋势)。则有:

但是由于信号有间断性，所以EMD分解会出现模态混叠的现象。由于模态混叠现象的出现造成了预测模型对分量的适应性下降。所以本文选用了能够改善其不足的EEMD方法。

1.1.2 EEMD算法原理

EEMD方法是 Z．Wu和 N．E．Huang等人在2005年为了改善混叠现象所提出的[3，4]。该方法是在EMD的基础上加入了高斯白噪声，高斯白噪声具有频率均匀分布的统计特性，所以它可以使信号在不同的尺度上具有了连续性，有效的避免了EMD分解过程中由于imf的不连续性而造成的混叠现象。其具体步骤为:

(1)原始数据序列中加入高斯白噪声;

(2)按照EMD的方法将加入白噪声的数据序列进行分解得到一系列的imf;

(3)重复的加入相同幅值的不同白噪声序列，重复(1)和(2)，把得到的各个imf取均值最为最终的结果。

1.2 粒子群优化算法原理

粒子群优化算法(Particle Swarm Optimization，PSO算法)是一种进化计算技术，由Eberhart博士和 Kennedy 博士发明[5～7]。

PSO算法首先初始化一群随机粒子(随机解)，然后粒子们就追随当前的最优粒子在解空间中搜索，即通过迭代找到最优解。假定d维搜索空间中的第i个粒子的位置和速度分别为Xi和Vi，在每一次迭代中，粒子通过跟踪两个最优解来更新自己，第一个就是粒子本身所找到的最优解，即个体极值pbest;另一个是整个种群目前找到的最优解，即全局最优解gbest。找到这两个最优解时，粒子根据式(2)、(3)更新自己的速度和新的位置。

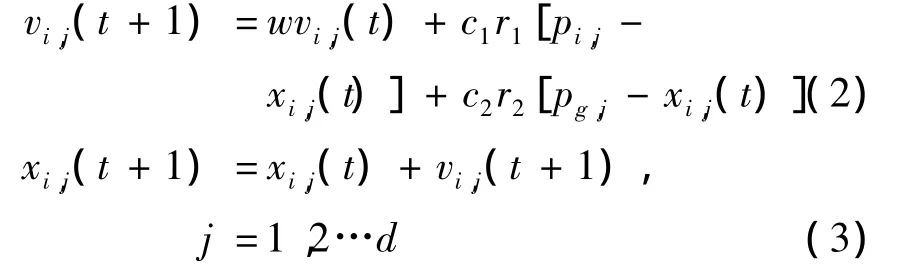
式中:w为惯性权重因子;c1和c2为正的学习因子，通常取c1和c2为2，但也有其他的取值，一般范围在0到4之间;r1和r2为0到1之间均匀分布的随机数。

1.3 支持向量机算法原理

20世纪90年代，由Vapnik首先提出支持向量机 (support vector machine，SVM)理论[8～10]。SVM是一种基于结构风险最小化原理的机器学习技术，具有较好的泛化性能。后来人们将其运用于回归问题，并取得了良好的效果。当SVM用于回归和预测时通常称其为支持向量回归机(SVR)。

对于一组线性数据样本集:

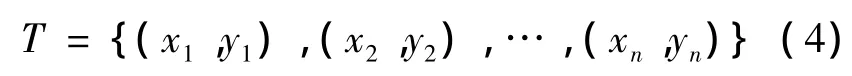
构造输入x与输出y拟合曲线方为

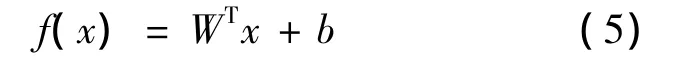
式中:W为权重系数;b为偏置项。

通过引入不敏感参数ε，松弛变量ξi，和惩罚因子C，将问题转化为对偶问题，利用二次规划方法求解该问题的优化问题。所以，引入拉格朗日乘子，将带有约束的优化问题转化成无约束优化问题:

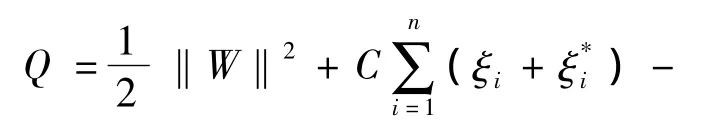
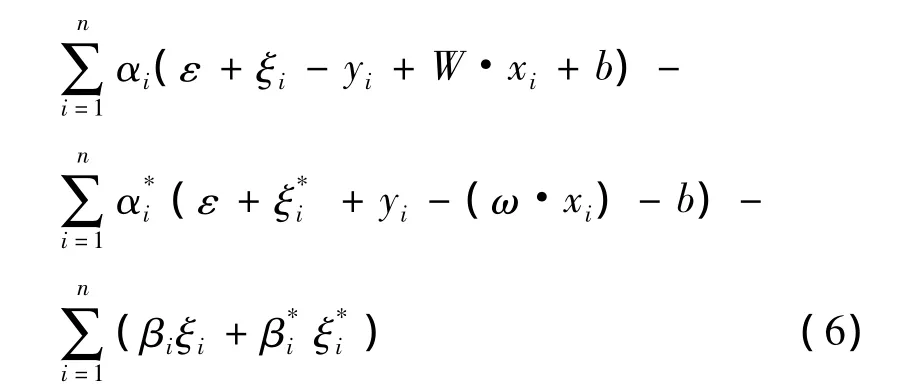
式中:αi，为拉格朗日乘子。对式(6)，W，b，ξi，求偏导，让其等于零，同时还应满足Karush-Kuhn-Tucker(KKT)准则，可得回归函数表达式:

当训练集为非线性时，引入径向基核函数K(xi·xj)，将低维非线性问题转化为高维线性问题。可以得到最优的非线性回归函数:

式中:K(xi，yj)=exp(－ ‖x － y‖2/2σ2)。

2 PSO优化SVM原理

惩罚因子C和核参数σ对SVM预测精度的影响较大，采用PSO优化SVM，选出最佳参数组合[11，12]。对于本文的案例来说，要对每个 imf分量和残余分量都要进行PSO优化SVM。步骤如下:

(1)随机初始化种群中个粒子的位置和速度，粒子向量代表一个SVM模型，该模型对应着的惩罚因子C和核参数σ。设置种群的大小为20，迭代次数为200，惯性权重w取1，c1和c2为2，C的寻优区间为[104，0.1]，σ 寻优区间为[103，0.001];

(2)用新确定粒子坐标位置(即SVM新的参数组合)，建立SVM预测模型。

(3)计算粒子的适应度，本文将平均误差作为适应度值。

式中:f表示粒子的适应度值;n为预测样本的个数;y为样本的真实值，x为样本的预测值。

(4)评价每个微粒的适应度值，将当前各微粒的适应度值的位置和适应度储存在各微粒的pbest中，将所有pbest中适应度最优值个体的位置和适应度值储存在gbest中;

(5)用上式(2)和(3)进行粒子的速度和位置的更新，新的粒子位置即为新的SVM参数组合;

(6)对每个微粒，将其适应度值与其经历的最好位置进行比较，将好的作为当前位置;比较当前所有pbest和gbest的值，更新gbest。

(7)判断所有粒子最优位置的适应度值和迭代次数是否满足条件，如果满足停止搜索，输出结果，否则返回步骤(2)继续搜索。

3 基于EEMD和PSO-SVM的短期风速预测模型

风速时间序列具有较强的随机性、非平稳性和非线性特点，因此使用常规的预测方法会产生很大的预测误差。本文根据EEMD对信号的分解特性、SVM的预测特点和SVM对参数的依赖特性，提出了EEMD和PSO-SVM的预测模型。首先对风速的时间序列进行EEMD分解，将其分解为若干个相对平稳的imf和残余分量之和;然后分别对各个分量建立PSO-SVM预测模型;最后将各分量的预测值相加得到最后的风速预测值。其具体步骤如图1所示。

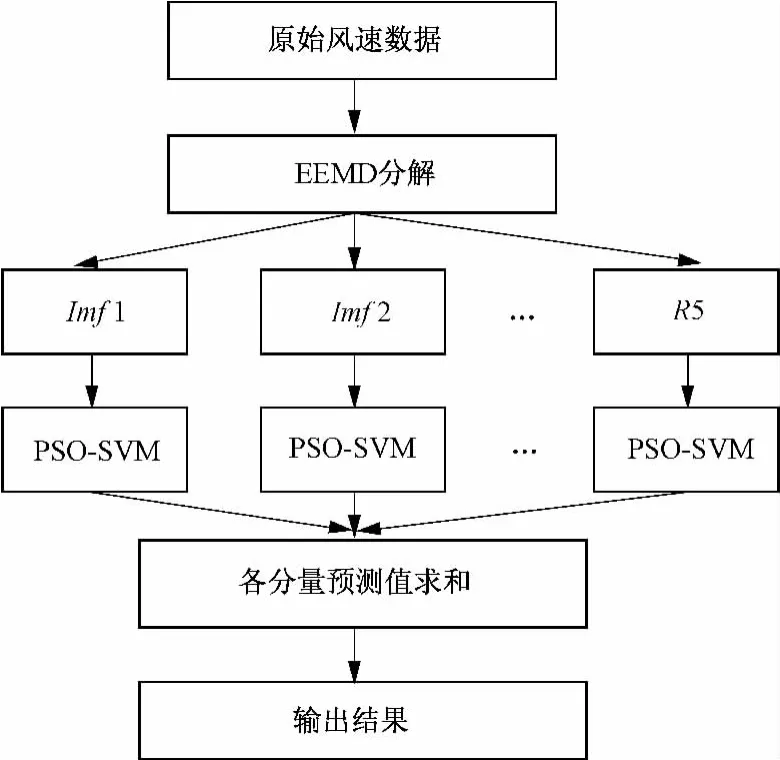
图1 本文的风速预测模型Fig.1 Wind speed prediction model in this paper

4 实验结果分析

本文以中国某风电场的实测数据样本为例。给样本的采样频率为10 min采样一个点，取其前120个采样点为实验数据。其中前100个采样点为模型的训练样本，后20个点为预测数据。图2为风速的原始数据。

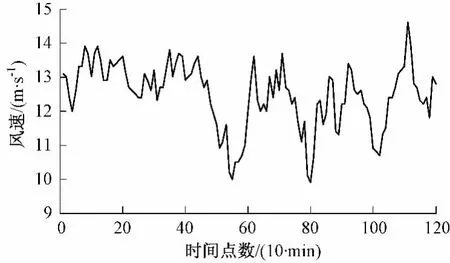
图2 风速的原始数据Fig.2 Raw data of wind speed

首先，对风速的原始信号进行EEMD分解，将其分解为 imf1，imf2，imf3，imf4，imf5 和残余分量r5，图3为前100个训练点的分解图。

图3 训练点的分解图Fig.3 Exploded view of training points

然后，将每个分量都作为PSO-SVM的输入特征，对每个分量都建立PSO-SVM预测模型，通过预测模型预测后20个点的分量值。表1为在分量的预测过程中经过PSO优化得到的SVM最佳的参数组合。以 imf1，imf2，imf3，imf4为例，图4为分量imf1，imf2，imf3，imf4的预测值与真实值的拟合图和平均误差的趋势图。

表1 参数组合Tab.1 Parameter combinations

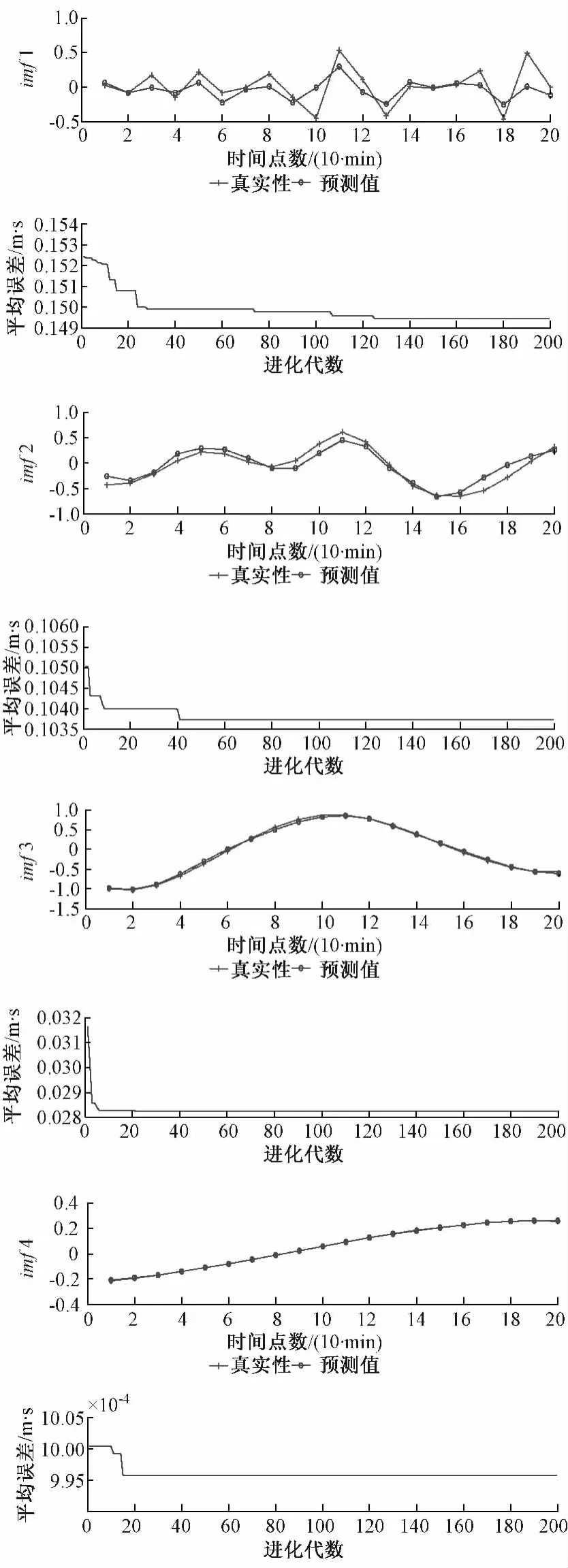
图4 各分量的预测值与真实值的拟合图和平均误差的趋势图Fig.4 Fitting diagram of prediction value and true value of each component and the trends of average error

将各分量的预测值相加得到风速的真实的预测值。同时本文还用SVM直接对风速数据进行预测，并与本文方法进行了比较。表2为两种方法预测值与真实值对比，图5为真实值与预测值的对比图。

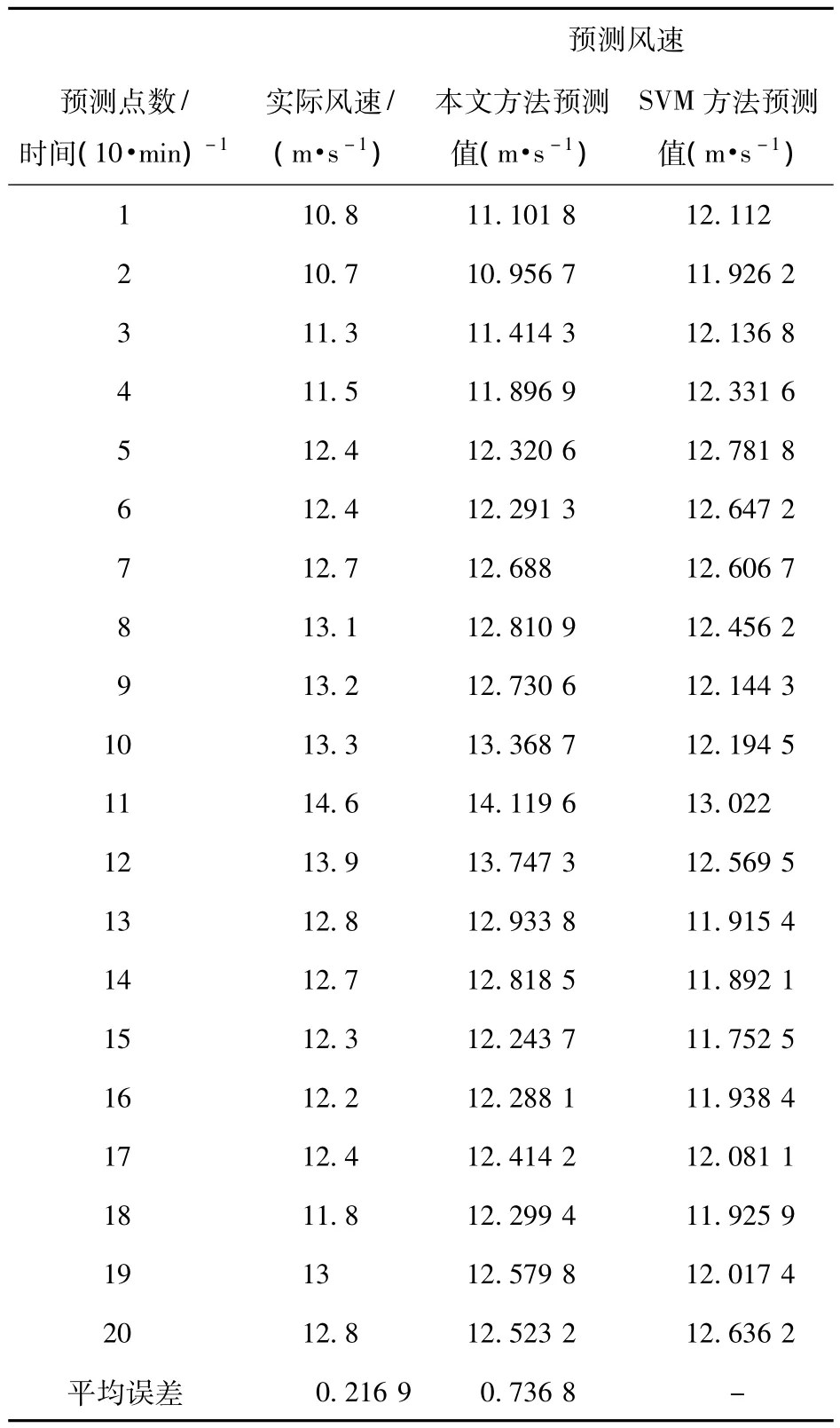
表2 预测值与真实值对比Tab.2 Comparison of predicted values and true values

图5 真实值与预测值的对比Fig.5 Comparison of true values and predicted values

从表2和图5可以清晰的看到，本文所用的预测模型比SVM直接预测模型预测效果好很多，预测精度有了很大的提高。虽然其中有些点的误差有些大，但是通过PSO对SVM优化寻找最佳的参数组合，已经很大程度上减小了误差值。

5 结论

本文提出的基于EEMD和PSO-SVM的预测模型。通过将非平稳的风速数据分解为一系列的imf分量和残余分量，将风速平稳化;并对每个分量分别建立经过PSO参数优化后SVM预测模型，进行数据预测。通过实验比较，此方法可以用于风速的短期预测，并且求得了比较好的预测结果。

[1]周志峰，胡秀娟．基于改进 EMD的汽车动态称重信号处理[J]．数据采集与处理，2009，23(6):751－755．

[2]韩中合，朱霄珣，李文华，等．基于 EMD消除Wigner-Vill分布交叉项的研究[J]．汽轮机技术，2010(003):211－214．

[3]刘岱，庞松岭，骆伟．基于EEMD与神经网络的短期负荷预测[J]．东北电力大学学报，2009，29(6):20－26．

[4]林近山．基于EEMD和Hilbert变换的齿轮箱故障诊断[J]．机械传动，2010，34(5):62－65．

[5]张丽平，粒子群优化算法的理论及实践[D]．杭州:浙江大学，2005．

[6]柴长松，张欣，牛奔，等．基于粒子群神经网络的发动机故障诊断[J]．微计算机信息，2007，23(22):186－187．

[7]夏晓华，金以慧，等．基于PSO的预测控制及在聚丙烯的应用[J]．控制工程，2006，13(5):1－3．

[8]刘向东，骆斌，陈兆乾．支持向量机最优模型选择的研究[J]．计算机研究与发展，2005，42(4):576－581．

[9]姚程宽．不平衡样本集中 SVM的应用综述[J]．计算机应用与软件，2008，25(9):1，2．

[10]何渊淘，邓伟．改进的不均衡样本集支持向量机预处理方法[J]．计算机工程与应用，2010，46(010):36－37．

[11]齐志泉，田英杰，徐志洁．支持向量机中的核参数选择问题[J]．控制工程，2005，12(4):379－381．

[12]邵信光，杨慧中，陈刚．基于粒子群优化算法的支持向量机参数选择及其应用[J]．控制理论与应用，2006，23(5):740－743．