基于Ucosφ和无功功率特征定位电网失步振荡中心的方法

胡永强，杨玉倩，赵书强，梁慧媛

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引言

电力系统长期运行实践表明，不论对稳定性的要求如何严格，总可能因一些不可预料因素导致稳定破坏事故。系统稳定破坏表现为同调机群间功角差不断拉大而失去同步，系统潮流和电压发生强烈振荡，且失步振荡主要发生于互联失步系统间或失步机组与主系统间的联络线上［1］。系统失步后，在失步振荡中心所在断面实施解列，一般可以保证解列后的子系统各自保持同步，并快速平息振荡，这是处理失步振荡的最有效手段，所以准确找到失步振荡中心位置很有必要。

目前国内外失步解列装置中应用的失步振荡中心定位方法，如测量视在阻抗最小值和最低电压幅值等方法［2～3］，多是基于两机系统模型的理论研究和单端就地电气量的测量，对于现今复杂互联的电力系统而言，已不能满足需要，且随着WAMS系统的广泛应用，如何利用PMU实时监测到的系统参数，并将其应用于失步振荡中心定位和失步中心的捕捉，提高失步解列的准确性，是一个值得研究的问题。

失步过程中失步断面联络线上电压最低点，被定义为振荡中心［4］。电压与无功功率有强耦合关系，无功功率特征可以反映电压变化，故本文从无功功率入手，提出定位失步振荡中心的方法。首先利用基于电流变化量的失步启动判据和Ucosφ主判据判定系统失步，并确定失步中心可能所在线路，继而利用线路两端母线电压相角差θ=180°时刻无功功率大小和符号判定失步中心所在位置。

1 基于Ucosφ和无功功率特征定位失步振荡中心的实现方案

对于实际复杂互联电力系统而言，若故障使系统呈现两群失稳模式，则不论网络如何复杂都一定存在振荡中心，但各元件的阻抗角不尽相同，所以振荡中心并非处于网络中某个固定的位置，但一定存在具有两机等值系统中振荡中心特征的支路也往往不是一两条联络线，而是一个断面，该断面即是与失稳模式相对应的临界割集［5］，确定这个临界割集，即可找出失步振荡中心所在线路。

1.1 基于电流变化率的失步启动判据

《电力系统安全稳定导则》中指出:“在电力系统出现失步状态时，应尽快解列失步机组或采取系统解列控制措施，在预定的联络断面将系统解列为两部分。”但对电力系统而言，因故障发生失步的时间很短，如果解列装置时刻都在进行失步判断和振荡中心定位，会增加其动作次数，而缩短使用寿命，故须设置启动判据，由PMU实时监测到的参数变化进行判断。

基于等值两机系统中对于电流变化规律的分析，系统发生失步时，线路电流仅和两端等值电势、功角差及系统总阻抗有关，利用电流状态量变化规律作为启动判据，具有很好的适用性，不受装置安装位置的影响。下面以10机系统失步振荡情况为例，观察故障清理不及时造成失步和故障及时清除后未发生失步两种情况下，某联络线电流的变化情况，分别如图1(a)和(b)所示:

(1)电流特征分析

如图1所示，在系统发生故障和系统失步时，联络线路上电流变化的情况会有明显的区别:当发生故障时，电流会迅速从正常电流增大到故障电流，并保持不变，故障切除后，电流迅速变小，并在很小的范围内做减幅摆动;当系统因故障切除不及时发生失步时，在故障切除后电流将做大幅摆动，因此，利用电流在一个振荡周期内的变化量，可以很好地将故障和失步振荡区别出来［6］。

图1 失步与未失步时联络线电流变化情况对比图Fig.1 Comparison of contact line current variation between out of step and normal occasion

(2)失步启动判据

基于电流变化量的启动判据为ΔIm≥Iset，传统判据中阈值的选取多通过离线计算，但增加PMU装置后，电网内发电机功角、线路电流均可以实时测量，可以实时对阈值的选取进行调整，具有很好的适用性。

(3)阈值分析

取联络线故障时短路电流与正常运行状态下电流之间的差值作为阈值Iset;当联络线两侧的等值功角差δ拉大到180°时，失步振荡电流幅值出现最大值Imax，当两侧的等值功角差为0°时，失步振荡电流幅值出现最小值Imin;一旦联络线电流变化量ΔIm=Imax－Imin大于阈值Iset，则启动失步判据 Ucosφ。

1.2 Ucosφ判据

根据《电力系统安全稳定控制技术导则》的规定:两个同调机群惯量中心等值发电机转子之间的功角δ摆幅超过180°即为判定该系统失去同步。传统Ucosφ判据原理为:对等值两机系统而言，功角 δ摆幅超过 180°即Ucosφ过零即可判定系统失步，且失步振荡中心就位于该条线路上［7～8］。

但对复杂电力系统而言，不可能容易地将相对失步的两同调机群等效为等值两机系统，也就不能直接测量等值发电机功角差的变化，所以在大多数情况下，可以用联络线两侧母线电压相量之间的相角差θ来近似反映功角差的变化规律［9］。所以复杂系统中，对于任一联络线，Ucosφ既可以反映联络线两端电压相角差θ的变化，又可以用于振荡中心的定位。

复杂电力系统中，虽然联络线两端电压相角差θ超过180°，即Ucosφ过零可以判定系统失步，但并不能说明失步振荡中心就位于该条线路上，其不足主要表现为:Ucosφ判据是基于等值两机系统的单端量判据，而在实际的失步振荡过程中，联络线两端等值电势是不相等的;基于Ucosφ只能部分捕捉振荡中心电压的变化特征，多机系统复杂的失步状况仅靠单端就地量的Ucosφ判据不能准确可靠地捕捉到［10］;假设Ucosφ单端判断某条预设联络线后确定系统失步，则振荡中心可能位于本条线路，也可能位于与其串联、并联或邻近的其他线路上，不能准确判定振荡中心位于之前预设的联络线上。

故本文拟定的实施方案中，采用Ucosφ作为主判据，判定系统失步，并且利用其判定结果划定振荡中心可能存在的线路，并对这些线路及与其紧密连接的线路进行二次筛选，应用无功功率的特征进行准确定位。

1.3 基于无功功率特征定位失步振荡中心

1.3.1 方法原理

无功功率与电压存在强耦合关系，且具有流动的方向性，因此可考虑利用无功功率特征判断失步中心位置。对Ucosφ判据筛选出来的线路及与其紧密相连的线路需进行再判断。

当联络线电压相角差θ=180°时，失步振荡中心也称失步中心，此时无功功率在失步断面联络线MN上呈单调分布，示意图如图2所示，且在失步中心处为零，与电压具有一致性关系［11］。

图2 无功功率分布示意图Fig.2 Reactive power distribution diagram

故可利用PMU测得的实时参数进行双端电气量的对比，从而判定失步振荡中心是否位于本条线路。原理如下:

如图3，PMU测量装置分别位于线路两端，定义电流正方向为由左侧母线流向线路。那么认为，若测量装置测得电流正方向流向失步中心，说明失步中心在测量点的正方向;反之则说明失步中心在测量点的反方向。若两端PMU同时分别测得失步中心在测量点的正方向和反方向，则说明失步中心位于本条线路，充分应用了PMU实时性的特点。

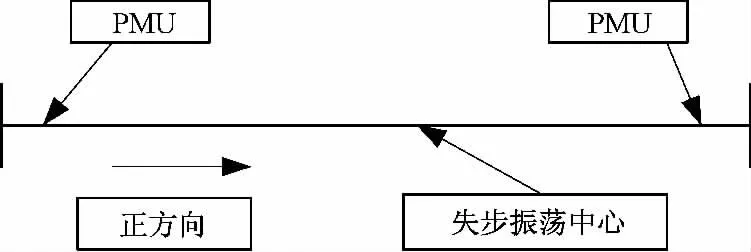
图3 测量点与失步中心位置关系图Fig.3 Position relationship between the measuring point and the out－of－step center

因为无功功率和电压电流有一致性关系，故同理针对θ=180°时刻对应的两端无功功率进行分析:PMU装置测量到的无功功率为正值时，说明失步中心位于装置安装处的正向;当装置所测量到的无功功率为负值时，说明失步中心位于装置安装处的负向。

1.3.2 θ=180°时刻的确定

对于简单两机系统可以直接测量发电机功角，并计算功角差δ，但是对于复杂电力系统并不适用。前文曾提及，以Ucosφ连续过零判定系统失步，可将Ucosφ过零时刻即联络线电压相角差θ过180°时刻，近似认为是同调机群惯量中心功角差δ=180°时刻。故在实际工程应用中，可利用在一次失步振荡周期中，Ucosφ轨迹过零时所测量的无功功率值去判断失步中心位置，能保证在最佳解列时刻同时确定最佳解列位置。

1.4 实施方案流程图和方法步骤

1.4.1 流程图

如图4所示即本文所述失步振荡中心定位方法在PMU广泛应用前提下的一种应用，其中Iset是电流变化量启动判据的整定值。

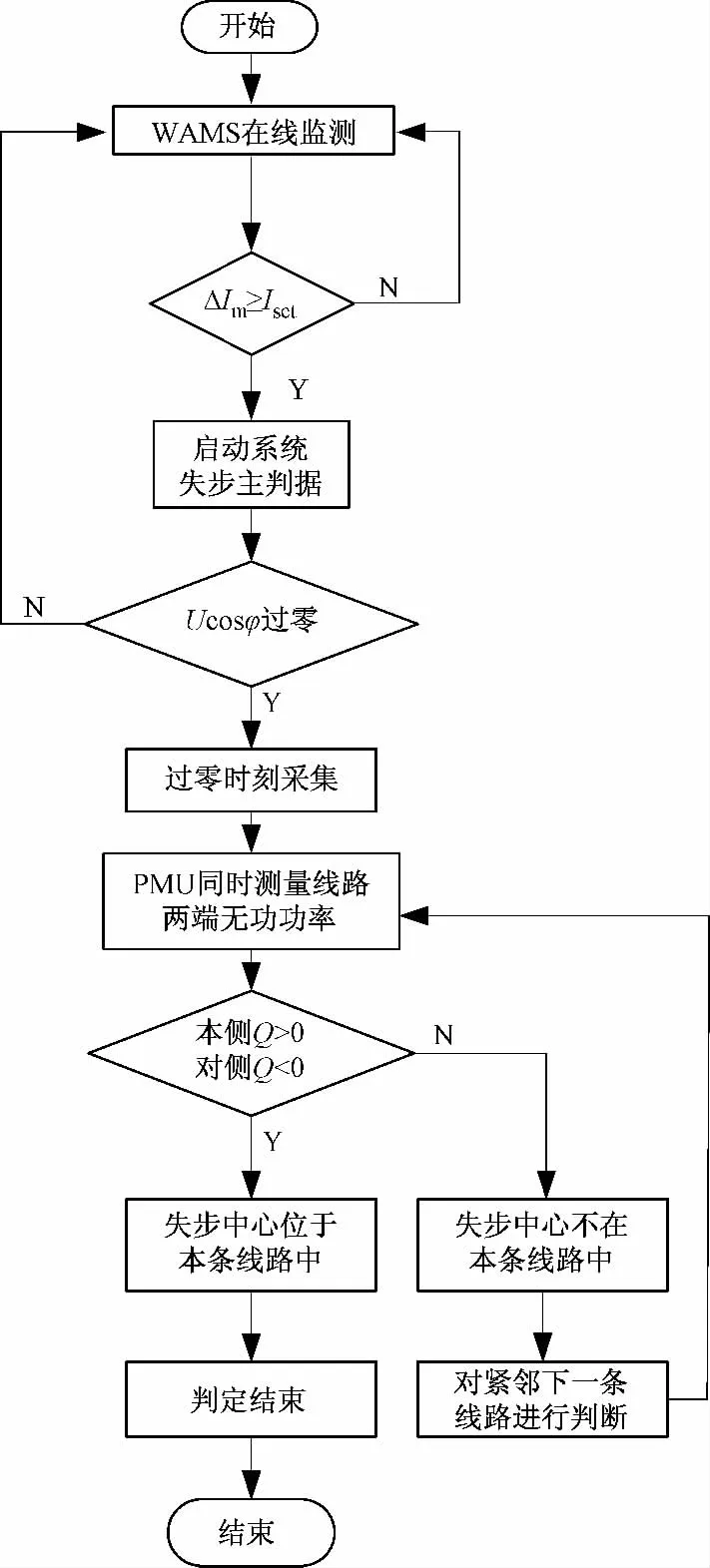
图4 流程图Fig.4 Flow chart

1.4.2 算法步骤

以电流变化量为启动判据，综合运用Ucosφ判据和无功功率特征研究失步振荡中心定位方法，如上流程图，其仿真计算步骤可以简述如下:

(1)进行多次仿真实验，针对发电机功角曲线，进行同调性分析，预设机群间联络线;

(2)失步启动判据:根据短路电流与正常运行电流的差值确定阈值Iset，无论是联络线还是是其周围线路，一旦发生电流大幅振荡，且电流变化量ΔIm＞Iset，则启动主判据;

(3)Ucosφ判据:针对研究施加的预想事故，进行暂态稳定仿真;根据预设联络线母线端电压、电流计算Ucosφ;连续跟踪Ucosφ的变化轨迹，满足预定的变化规律就判为失步，且失步振荡中心位于该线路或附近线路，同时采集Ucosφ过零点时刻;

(4)基于无功功率特征定位失步振荡中心:对(2)中得出的线路及其紧密联系的线路进行再判断，根据Ucosφ过零时刻无功功率在线路上的单调性分布特点，通过测量线路两端无功功率值正负判定失步振荡中心是否位于本条线路。

2 仿真算例

利用电力系统电磁机电暂态混合仿真程序(DIgSILENT/PowerFactory)为仿真工具，对新英格兰10机39节点系统仿真模型进行暂态仿真研究，该模型是电力系统暂态稳定分析的典型模型，在发生失步后的暂态过程中各电气量变化规律明显，且易于在失步机群间预设联络线，有助于失步振荡的观察和分析。该系统有10台发电机、39个节点、34条线路和12台变压器，其接线如图5所示，原始数据参考文献［12］。发电机Gl代表一个与新英格兰系统相连的外部系统，G2作为参考机组，考虑发电机励磁和原动机调速系统对系统的影响，负荷采用恒阻抗模型。

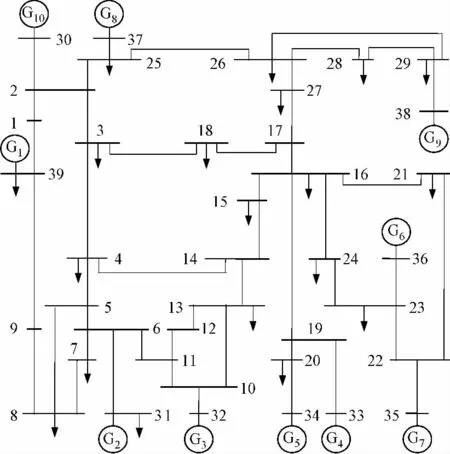
图5 新英格兰10机39节点系统Fig.5 New England 10－unit 39－bus system

设置复故障:0 s时线路L13－14在1%处发生三相短路，0.2 s清除故障不成功，1 s线路被切除，0.5 s线路 L2－25在50%处发生三相短路，0.59 s切除线路，系统出现失步振荡。图6所示是其他机组相对于机组2的功角轨迹曲线。

(1)观察发电机功角变化曲线，发电机G1，G10，G4～G9相对于G2相继失步，可预设系统联络线为 L4－5，L13－14，L8－9。

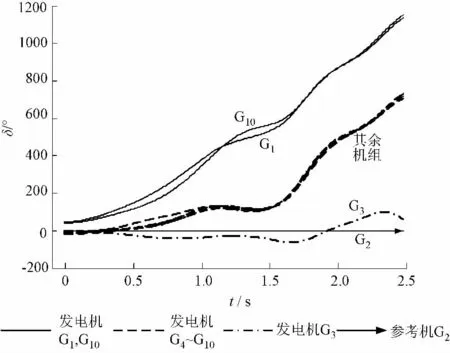
图6 发电机功角曲线Fig.6 Curve of power angle of generators

(2)电流变化量启动判据

首先观察所有线路电流的变化情况，发现系统失步后，线路 L4－5，L5－6，L6－11，L10－11电流做幅值很大的摆动，而不是故障切除后做减幅摆动，分别如图7 中(a)、(b)、(c)、(d)所示。

根据1.1中所述阈值设定方法，通过 DIgSILENT仿真，可以得到系统故障运行时预设联络线的电流参数，以预设联络线L4－5为基准，故障电流最大值为Imax=1.3 kA，正常运行时电流幅值为Imin=0.27 kA，则可设置电流变化量启动判据的阈值为Iset=Imax－Imin=1.03 kA。

以L5－6为判定对象，系统正常运行时电流为0.8 kA，故障发生瞬间，电流增大为1.64 kA，且在故障中基本保持不变，略微降低，变化量为ΔIm=1.64－0.8=0.84 kA＜Iset，不满足失步判据大于Iset的要求，失步判据不启动;故障切除后，电流发生大幅振荡，范围在0.14 kA和3.78 kA之间，电流变化量ΔI=3.78－0.14=3.64 kA ＞Iset可以启动判据。而且只要有一条线路满足启动判据，则失步主判据Ucosφ启动。

(3)Ucosφ 判据

观察功角摇摆曲线，可以发现，以G2为参考机发电机G1和G10先失步，随后其余机组相继失步。系统预设联络线为 L4－5，L13－14，L8－9，它们与失步部分有紧密的电气联系，对这几条线路分别执行Ucosφ判据，由于 L13－14在处理故障时被切除，不予考虑。观察线路 L4－5，L8－9Ucosφ 曲线，分别如图8中(a)、(b)所示。

可见，两条线路均满足Ucosφ判据，即Ucosφ连续过零，说明系统失步，同时应捕捉过零时刻，线路 L4－5在 t=0.595 s时刻 Ucosφ 过零，线路L8－9在 t=0.642 s时刻Ucosφ 过零，因为只进行了单端Ucosφ判定，故将失步中心的范围划在这条线路及其周围几条线路上，继续进行基于无功功率特征的再判定。

图7 电流发生大幅振荡的线路电流变化曲线Fig.7 Current curve of lines which appears large oscillation

(4)对线路 L4－5和 L8－9分别在 t=0.595 s 和0.642 s时刻的两端无功功率瞬时值进行测量，汇总(如表1):

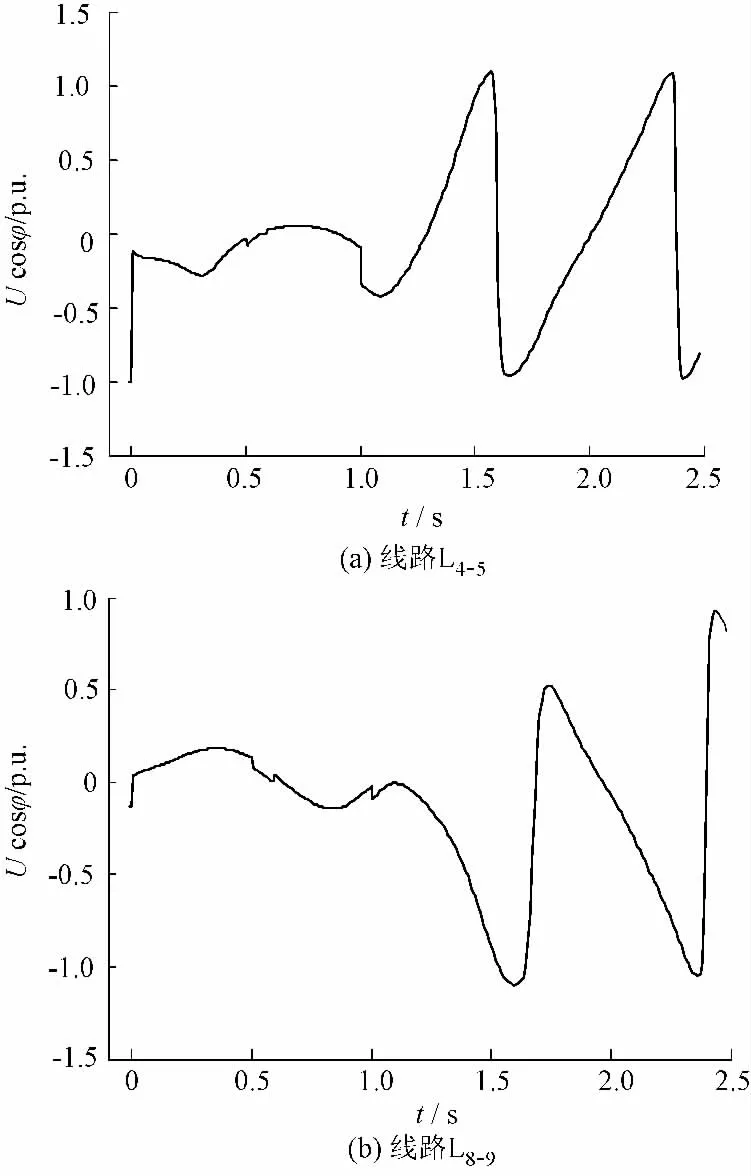
图8 预设联络线Ucosφ变化曲线Fig.8 Curve of Ucosφ of default contact lines

表1 Ucosφ过零时刻联络线两端无功功率值Tab.1 Reactive power value at both ends of the contact line when Ucosφ crosses zero

可见，对预设的联络线通过Ucosφ判定后，并未现失步中心落在预设联络线外的情况，L13－14在故障处理过程中被切除，故不再进行无功功率特征的再判断。由上可以判定失步中心落在线路L4－5和L8－9上，在上述时刻解列线路应该是较为合适的选择。如果一旦出现以上线路两端无功功率值并不满足符号相反，则要在紧邻线路进行再判断，以便准确捕捉失步中心。

3 结论

本文提出了一种综合运用电流、电压、无功功率特征判断失步振荡中心位置的方法，该方法综合系统实时运行状态，以Ucosφ作为反映失步振荡时电压相角差变化和振荡中心电压变化的主判据，以无功功率的正负反映失步中心的位置方向，经两者共同判定，可以更准确地识别系统失步振荡中心位置，弥补复杂电网中Ucosφ单端判定失步振荡中心的不足，进而协调配合解列装置，保证解列动作的可靠性。仿真结果表明该综合判定方法能很好地达到判定失步振荡中心位置的目的，并为系统解列提供时间和位置的有效参考。准确快速地找到失步振荡中心位置为快速解列以平息系统振荡提供可靠的依据。这种基于双端多电气量的综合定位方法对于广泛应用WAMS的复杂电网也具有良好的适用性。

［1］薛禹胜.现代电网稳定理论和分析技术的研究方向［J］.电力系统自动化，2000，(7):1－6.

［2］丛伟，潘贞存，肖静，等.电力系统振荡解列原理的分析与研究 ［J］.继电器，2003，31(10):51－55.

［3］董希建，赵杰，凌超，等.基于相位角原理的失步振荡解列判据机理研究 ［J］.电力系统保护与控制，2010，38(7):1－6.

［4］高鹏，王建全，周文平，等.关于振荡中心的研究［J］.电力系统自动化学报，2005，17(2):48－53.

［5］赵金利，余贻鑫.电力系统电压稳定分区和关键断面的确定［J］.电力系统自动化，2008，32(17):1－5.

［6］董建强.基于PMU的大区电网间失步解列方法的研究 ［D］.北京:华北电力大学，2006.

［7］Li Li， Yutian Liu.Out－of－step splitting framework based on adaptive separation detecting criterion ［J］.IEEE T＆D Asia 2009.

［8］姚李孝，宁卜，沈东方，等.异步运行状态下振荡中心研究 ［J］.电网与清洁能源，2008，24(6):16－20.

［9］李莉.基于广域测量信息的失步解列判据和控制方案研究［D］.济南:山东大学，2009.

［10］张保会，张毅刚，刘海涛.基于本地量的振荡解列装置原理研究 ［J］.中国电机工程学报，2001，21(12):67－72.

［11］高鹏，杨梅强，任祖怡.一种捕捉失步中心位置的新方法［J］.江苏电机工程，2006，25(3):7－10.

［12］Pai M A.Energy function analysis for power system stability analysis by the direct method of Lyapunov［M］.Boston:Kluwer Academic Pub，1968.