基于Simulink高阶非线性控制系统相平面实现

丁 红

(鲁东大学信息与电气工程学院，山东烟台264025)

0 引言

所有的控制系统都不同程度存在某种非线性特性。当非线性因素较弱时，非线性系统可以通过线性化方法按线性系统来处理，当非线性因素较强时，只能用非线性代数方程或非线性微分方程来描述。

在“自动控制原理”课程中，非线性系统的相平面法既能提供稳定性信息，又能提供时间响应的信息，通过相平面上相轨迹的运动趋势来确定非线性控制系统的动静态性能。但相平面法只适用于一阶、二阶线性环节组合而成的非线性系统，对于高阶线性环节组合而成的非线性系统则较难实现［1］。绘制一阶或二阶系统的相平面图的方法通常用δ法或等倾线法来实现。在有些文献中也阐述了高阶系统用δ法或等倾线法绘制高阶系统相平面图的方法，但还是较复杂的［2，3］。

本文介绍的绘制非线性系统相平面图的方法是在Simulink仿真环境中实现的，不但可以绘制一阶、二阶系统相平面图，还可以通过将线性系统部分化成能观标准形的形式，从而构造仿真模型，实现高阶系统的相平面图的绘制。这种方法简单实用，易于操作。

1 一般非线性系统的相平面图

对于一般的非线性系统，只要在Simulink中构造出仿真结构图，就可以得到相平面图。

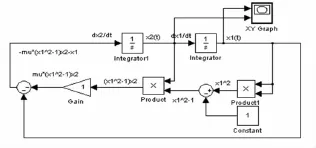
图1 范德堡方程仿真结构图

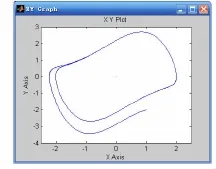
图2 输出的相轨迹图

2 高阶非线性系统相平面图的绘制

典型的非线性系统结构图如图3所示，其中线性系统的传递函数一般形式可以表示为

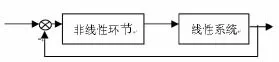
图3 非线性系统的结构图

设系统的输入为u，输出为y，则系统的微分方程形式为

设状态变量为

将x1……xn求导并整理得到能观标准形如下：

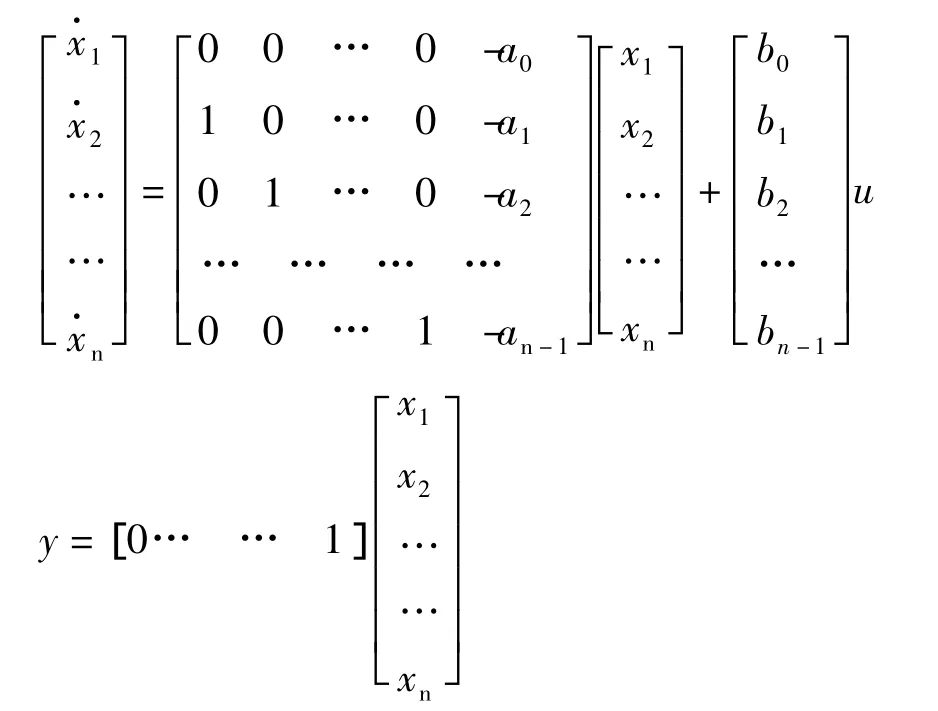
可以看出，能观标准型的特点是输出量等于最后一个状态变量xn，所以状态变量图中最后一个积分器的输出就是系统的输出量y，积分器的输入端是系统输出量y的一阶导数。而绘制系统的相平面图就是要在已知输出及各阶导数的初始条件下，绘制输出y和的相平面图，即(y，)平面的相轨迹。这样通过将线性系统部分化成能观标准形后，就可以得到输出y和，然后将其作为Simulink工具箱中的xy Graph模块的输入端，再将系统的仿真结构图构造出来进行仿真，相轨迹图就一目了然的绘制出来了。

其他形式的状态空间表达式中的输出y并不一定是某个状态变量，而大多数情况是等于状态变量的组合，所以将系统化成能观标准型，才能将输出y表示成状态变量xn，从而实现高阶系统的相平面图形的绘制。

3 仿真举例

下面还以图3所示的非线性系统为例说明绘制高阶系统相平面图的方法。线性部分的数学模型为

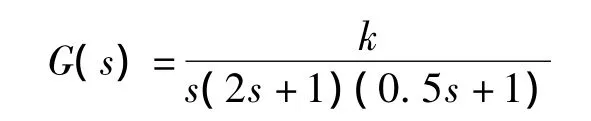
非线性部分具有饱和特性，其饱和特性的线性区域为［-1，1］，饱和值为 m=1，初始条件为

［y(0)(0)(0)］=［0.6，1，0.7］，由式(1)得［x1(0)，x2(0)，x3(0)］=［3.8，2.5，0.6］。

首先，将线性系统部分化成能观标准型：

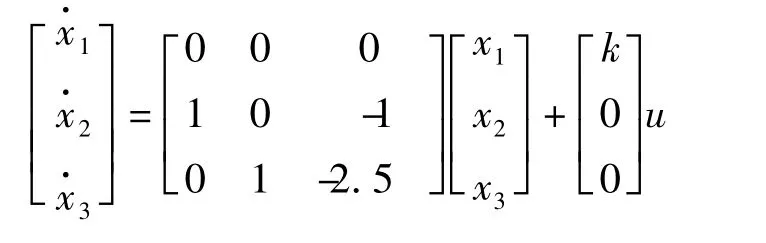
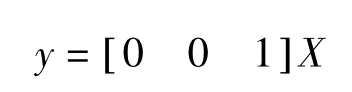
在Simulink环境中构造非线性系统的仿真结构图如图4所示。我们取不同的k值进行仿真发现，当k较小时，系统输出可以稳定于奇点［0，0］点，且k越小稳定的时间越短;当k大于等于2.5时，系统趋于某一极限环。

图4 非线性系统的仿真结构图

图5(a)和(b)分别给出了k=1.3时系统在初始条件为［y(0)，(0)，y¨(0)］=［0.6，1，1.7］，即［x1(0)，x2(0)，x3(0)］=［3.8，2.5，0.6］的相轨迹和输出响应。相轨迹的横轴为输出y，纵轴为。可以看出，相轨迹由初始条件出发，沿着稳定的方向以螺旋线方式最终趋于稳定，由图5(b)的输出响应也可以看出，系统稳定于原点。

而图6(a)和(b)所示为k=4.5时系统在同样初始条件下的相轨迹和输出响应。可以看出相轨迹由初始条件出发，沿着不稳定的方向趋于极限环，并且横轴输出呈等幅自振状态，其振幅为A=2.5。由图6(b)也可以看出输出自振的振幅为2.5，和相平面图是一致的。

用描述函数法分析可知，系统出现自激振荡的的临界k值为2.5，当k＜2.5时。系统趋于稳定。当k＞2.5时系统出现自激振荡。从图5和图6可以看出系统的相轨迹与描述函数法分析的结果是一致的，说明本文提出的基于Simulink仿真环境绘制高阶非线性系统相平面法是正确的。

另外，在Simulink环境中的非线性模块中(discontinuities)非线性环节包括很多种，如继电器特性、死区特性等等，可以直接调用及修改参数。也可以如图1所示，在Simulink中将非线性环节的仿真模块构造出来后，再将线性部分化成能观标准型，按上述方法构造仿真模型即可绘制出任意阶次系统输出的相平面图。其实，在Simulink仿真环境中绘制相平面图可以非常方便地得到任意变量相轨迹图。如图4所示，用积分器的输入和输出端作为示波器XY graph1和XY graph2的输入端，仿真就可以得到任意变量的相轨迹图，同时在输出加入一个示波器就可以得到系统的输出响应，如图5和图6所示。

图5 k=1.3时仿真结果

图6 k=4.5时的仿真结果

4 结语

本文介绍了借助Simulink绘制系统的相平面图形的问题。我们只要将系统的仿真结构图构造出来，将积分器的输入端和输出端作为示波器的输入，通过仿真就可以得到系统中任意变量的相平面图。对于高阶系统，采用将非线性系统中的线性部分化成能观标准型，将非线性部分用Simulink中的非线性模块或构造非线性系统仿真模型的方法，就可以实现高阶系统的相平面图的绘制，使传统的只适用于一、二阶系统分析的相平面法推广应用到高阶非线性系统中。该方法简单实用，易于实现，扩大了相平面法的应用范围。

［1］胡寿松.自动控制原理［M］.北京：科学出版社，2001

［2］张德祥等.高阶非线性控制系统相平面的图解实现［J］.北京：系统仿真学报，2005.(17)12

［3］张德祥等.基于δ法高阶非线性系统相平面实现［J］.北京：系统仿真学报，2004.16(4)

［4］薛定宇.基于Matlab/Simulink的系统仿真技术与应用［M］.北京：清华大学出版社2002