直觉分析在电路教学中的应用

田社平，张 峰，陈洪亮

(上海交通大学电子信息与电气工程学院，上海200240)

“电路理论”或“电路分析”课程是电类专业的第一门专业基础课，学生对该课程掌握的质量直接影响后续电类课程的学习。在教学中，除了要让学生掌握电路分析的基本知识外，还要培养学生的电路分析的各种能力。B.Razavi指出：“好的模拟电路设计依赖直觉、缜密和创造。作为模拟电路设计师，应该拥有工程师的直觉，能够快速地、直觉地理解一个大型电路;拥有数学家的缜密，能够计算出那些对电路虽然微小但却重要的影响;拥有艺术家的创造，能够发明新的电路拓扑形式”［1］。可见，直觉分析能力是一种综合能力。可以说，直觉分析能力的培养是目前高等教育教学中非常重要而又经常被忽视的实践内容，它与逻辑思维能力的培养有着同样的甚至更为重要的地位和作用［2］。在电路教学中，我们往往注重电路的逻辑分析能力的培养，而减弱甚至忽视其他方面的能力，如直觉分析能力。在国外的电路教学中，则非常重视电路直觉分析的教学，例如美国麻省理工学院(MIT)的电路与电子学教材专门将电路的直觉分析列为教材的内容［3］。在电气工程领域，同样也十分注意直觉分析方法的应用［4，5］。本文结合教学实际，通过举例说明电路直觉分析方法的表现形式以及如何开展电路直觉分析的教学。

1 直觉分析的特点

人们在分析和处理问题的时候，除了采用逻辑思维方式外，还会采取一些非逻辑性的思维形式。直觉思维是一种重要的非逻辑性思维形式。所谓直觉，是指一种不经过分析、推理的认识过程而直接快速地进行判断的认识能力。一般认为，直觉分析具有如下特点。

(1)直接性—主体不通过一步步的分析过程而直接获得对事物的整体认识，这是直觉思维最基本和最显著的特征。

(2)快速性—指思维的结果产生得很迅速，这种快速性以致思维者对所进行的过程无法作出逻辑的解释。

(3)跳跃性—在认知过程中，逻辑性思维是以常规的方式按步骤展现的，而直觉思维摆脱了这种常规的束缚，从而产生认知过程的急速飞跃和渐进性的中断。

(4)个体性—与思维者的知识经验和思维品质相联系，表现出直觉的个体特征。

(5)坚信感—主体的直觉分析有别于冲动性行为，主体对直觉结果的正确性或真理性具有本能的信念。当然，这并不意味着取消进一步分析加工和实验验证的必要性。

(6)或然性—非逻辑思维是非必然的，有可能正确，也可能错误，表现出直觉思维的局限性。

2 直觉分析的三种表现形式

2.1 直观分析

直观，即感性认识，就是实践中外界事物作用于人的感觉器官而在大脑中产生的感觉、知觉和表象，其特点是生动性、具体性和直接性。直观分析就是采用简单的易于理解的手段或方法如图表等进行的分析，其特点是理解上一见即明。

如图1(a)所示为RC高通正弦稳态电路，要判断输出电压与输入电压之间的相位关系，我们作出图1(b)所示的相量图。从图1(b)可以非常直观地看出各电压相量的相位关系。我们不难得出输出电压相位超前输入电压相位的结论。可见正弦稳态电路的相量图分析方法就是一种直观的分析方法。

图1 RC高通电路及相量图

2.2 抽象直觉分析

通常所说的抽象，是指在认识上把事物的规定、属性、关系从原来有机联系的整体中孤立地抽取出来。通过抽象，可以在更深的层次上把握事物的规律。对电路分析而言，除了在直观上理解电路的概念、方法和定理以外，还应考虑在一定的抽象层次上的直觉掌握和理解，特别是对于一些特殊的数量关系和规律，可以放弃其形成过程的逻辑关系，而直接从数量关系构成对象的数量特征出发，对其加以理解和把握，我们称之为抽象直觉分析。

例如，直流激励的一阶电路的三要素法的表达式为

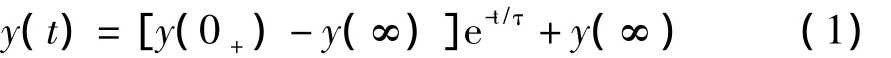
式中，三要素y(0+)，y(∞)和τ分别为初始值、稳态值和时间常数。

三要素法是跳过建立电路微分方程，直接由给定的一阶电路求三个要素，并列写出响应的数学表达式。这种方法是在总结了一阶电路全响应解析式结构规律的基础上得出的。撇开实际的一阶电路，可以对式(1)作如下的抽象直觉理解和分析。

(1)一阶电路中的响应是按指数规律变化的，都有它的初始值和稳态值，其变化过程惟一地由时间常数决定。

(2)基于上述认识，可以一般地写出一阶电路的响应形式：

(3)利用y(t)|t=0+=y(0+)和y(t)|t=∞=y(∞)的条件，可以写出

通过以上三点的分析，可以得到式(1)的结论：上述分析抛开了具体的电路，直接抓住一阶电路中特殊的数量关系和规律，一阶电路的响应仅与三个要素相关，其响应形式按指数规律变化。

2.3 创造性直觉分析

这是直觉分析能力中最高层次上的一种分析能力，直觉思维表现在对于客观存在的事物、现象、过程、系统中存在的量的方面的直觉的认识和把握，能够直觉地看出所隐含在其中的数量对象、数量关系、数量的变与不变的变化规律，这实际上就是抽象思维的过程。因此，创造性直觉分析能力是一种综合的能力，它是在对复杂分析对象进行类比、联想、发散、添加、数理演算、对比和猜想等良好的思维习惯和思维意识培养过程中逐步形成的［6］。

如图2(a)所示电路中，已知R=2Ω，C=0.5F，uS=e-3tε(t)V 时，其零状态响应当为u=(0.1e-0.5t+0.6e-3t)ε(t)V。现将R换成1Ω电阻，将C换成0.5H的电感，uS换成冲激电压源uS=2δ(t)V，求零状态响应u。

这是一道常常让学生感到疑惑的难题［7］。其难点在于电路的拓扑结构未知，而且要将RC支路替换为RL支路后再求响应，问题较为复杂。观察电路可知，如果将RC支路看作为一条阻抗支路，则将RC支路替换为RL支路后，只是该支路的阻抗发生了变化。图2(b)的S域模型使问题得到化解，这就是一种典型的直觉思维。在此基础上作进一步分析不难得出正确答案。

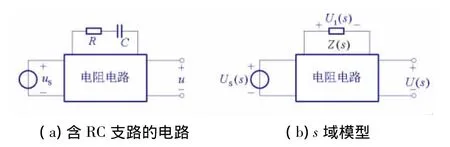
图2 创造性直觉分析示例图

3 电路教学中直觉分析能力的培养

直觉分析能力是一种可以培养的能力。对电路课程而言，我们认为可从如下几个方面着手。

(1)强化基础知识的教学

电路课程的基本概念多，分析方法灵活，只有深刻理解基本概念和熟练掌握各种分析方法，才有可能为提高直觉分析能力打下基础。在实际中，常常出现这样的情况：对某一问题，有的人往往不知从何处下手，甚至花费很长时间也不得要领，但另外的人可能用手一点，就指出问题的症结所在，问题立刻迎刃而解。这些人似乎凭直觉就知道问题的关键。其实，这就是一种直觉能力的表现，它是以深厚的基础知识作为铺垫的。

(2)注意电路分析方法和规律的总结

在教学过程中，不仅要加强基本概念的教学，还要注意电路分析方法和规律的总结。光知道基本概念，但不知道如何在电路分析中运用这些基本概念，那就根本谈不上能力的提高

(3)加强电路分析能力的训练

直观分析能力体现在对各种电路知识和方法的融会贯通上。要做到这一点，必须进行必要的电路分析的练习和训练。只有对电路分析方法的熟练掌握，才能又快又巧地解决碰到的电路问题。我们的体会是要适当引入对电路综合问题甚至是电路难题的讲解。

在教学中，还应当适当安排一些时间介绍电路发展史上的一些科学探索的实例，培养学生良好的科学素养，引导学生进行积极的思考，使其不断产生出突然获取问题解答的直觉状态。这种科学素质的培养是不可或缺的。

(4)加强实践教学环节

直觉分析能力在工程师中表现得最为明显，这是因为工程师拥有大量的解决工程实际问题的实践，积累了大量的经验。面对新的工程问题，我们可以快速直觉地给出问题解决方案。在电路教学中，可以通过加强实践教学环节，加深对电路基本概念和基本分析方法的理解。特别是随着电路仿真软件的广泛应用，通过仿真的方法来观测电路运行的规律非常方便，对大型电路的分析尤其如此。

4 电路课程的应用效果

笔者在2012年年初向我校申请了一个有关直觉分析的教改项目，获批后在2012-2013教学年度第二学期电路课程教学中实施。

(1)在绪论课中简单介绍直觉分析的含义，列举科学研究中的一些关于直觉的例子，让学生对直觉和直觉分析有一定的认识。如美籍华裔物理学家丁肇中在直觉的驱使下决定研究重光子，终于发现了J粒子，并因此而获得诺贝尔物理学奖。又如，居里夫人在深入研究铀射线的过程中，凭直觉感到铀射线是一种原子的特性，通过检查所有已知的化学物质，不久就发现另外一种物质—铣也能自发地发出射线，与铀射线相似。

笔者还介绍了自己切身经历的一些例子。如在和企业工程师接触中，发现他们对一些工程中的问题具有极强的直觉分析能力，他们往往能够跳过分析快速地给出一些结论。

(2)在接下来的授课中，注重电路问题直觉分析的可能性。在基本概念、基本方法的讲解中尽可能突出直觉分析的作用;另一方面，在举例分析，总是询问“从直觉的角度，这个电路问题学生会不会分析?应该如何分析?”。下面举一例加以说明。

在给定电源内阻抗和负载阻抗的情况下，能否通过电路设计实现负载阻抗获得最大功率呢?这个问题可以通过直觉的方法加以分析。

回答上述问题无非有“是”或“否”两种答案。如果回答是，就要找到一个电路设计方案;如果回答否，这是基于教材中的最大功率定理这一结论而得出的。最大功率匹配或共轭匹配是针对电源和负载直接相连这种情况而得出的，因此从直觉上分析，如果在电源和负载之间接入一个电路，有可能改变负载吸收的功率。既然负载吸收的功率会变化，那就存在最大值的可能性。

基于上述直觉分析，不妨设计如图3所示的电路，即在电源和负载之间接入一个二端口网络N，以达到实现阻抗变换的目的。图中ZL=RL+jXL为负载阻抗，ZS=RS+jXS为电源内阻抗，均为给定;N为某一合适的二端口网络，待求。

图3 最大功率传输

电路N应有什么样的拓扑结构?由什么元件构成?从直觉上可从两方面加以分析：首先，N不应包含电阻元件，因为电阻元件为耗能元件，这样负载功率吸收的效率只能降低;其次，能否设计N，使得从N的右边向左端看去的阻抗与ZL得到最大功率匹配，或者从N的左边向右端看去的阻抗与ZS得到最大功率匹配。

至此，直觉分析过程完成，接下来就可以在上述直觉分析的基础上作进一步的逻辑分析。当然，并不是所有的电路问题都可以采用直觉分析方法。但笔者认为，电路问题的直觉分析例子可以说比比皆是。在教学中，笔者准备了二十多个电路直觉分析例子并加以讲解，取得了如下基本效果。

(1)绝大多数学生对直觉分析方法非常感兴趣，认为它是一种有趣的方法，但同时也认为似乎是一种高级的有点难掌握的方法。笔者在教学过程中曾组织过一个小调查，请学生提出一个最感兴趣的关于课程的问题，其中就有不少学生提到“如何才能具备电路的直觉分析能力?”

(2)一部分学生的直觉思维能力得到了锻炼。相比往届教学而言，笔者发现在本届教学中，学生提出的问题多，而且往往有一定深度。例如，对一阶RC充电电路，教材上介绍其能量效率为50%。有学生指出，有可能将能量效率提高，使其超过50%。我们认为这其中就包含有可贵的直觉思维，尽管该学生还暂时不知道答案。但该学生的直觉分析是值得鼓励的［8］。

5 结语

(1)电路的直觉分析方法是一种综合的分析方法，它建立在对电路基本概念和基本分析方法深刻理解和熟练掌握的基础之上，是一种可以在教学活动中进行讲授的方法。

(2)通过在电路教学中适当加入直觉分析的例子，并加以适当引导，可以锻炼学生的直觉思维能力，同时还可以提高学生学习电路的积极性。

(3)一门课程的教学是一个综合的过程。值得指出的是，我们提倡电路的直觉分析，并不意味着我们否定其他分析方法和分析能力的培养。

［1］Behzad Razavi.Design of Analog CMOS Integrated Circuits［M］.Columbus：McGraw-Hill，2001

［2］亓正坤.浅谈数学直觉思维在高等数学教学中的培养［J］.兰州：高等理科教育，2006(3)：3～6

［3］Anant Agarwal，Jeffrey H.Lang著，于歆杰，朱桂萍，刘秀成译.模拟和数字电子电路基础［M］.北京：清华大学出版社.2008

［4］Darren Ashby.Electrical Engineering 101：Everything You Should Have Learned in School but Probably Didn＇t［M］.Singapore：Elsevier，2006

［5］Marc T.Thompson.Intuitive Analog Circuit Design［M］.Elsevier，2006

［6］胡京爽.浅谈数学教学过程中逻辑、形式与直觉方法的表现［J］.合肥：工科数学.2001，17(6)：63～66

［7］陈洪亮，张峰，田社平.电路基础［M］.北京：高等教育出版社.2007

［8］陈希有，李冠林，刘凤春.RC电路充电效率分析［J］.电气电子教学学报.2012，34(2)：32～35