有零点二阶系统的动态性能分析

赵 耀，王 建，杨晓梅，曾晓东

(四川大学电气信息学院自动化系，四川成都610065)

0 引言

“自动控制原理”是自动化以及相关的专业的主干必修课程，也是分析和设计自动控制系统的入门课程，是所有后续控制类课程的基础。该课程的时域分析部分，通过对低阶及高阶系统典型响应的分析，可以建立起系统传递函数相关参数与响应性能之间的定性和定量关系，从而为后续的系统分析与设计奠定基础。

“自动控制原理”课程中的一阶系统分析比较简单容易，而代表性更广的二阶系统始终占据着时域分析这部分的核心地位。很多实际系统都可以近似为二阶系统，而且很多情况下反馈控制系统的设计可以归结为二阶系统的参数配置问题，常常还会涉及到零点的配置问题，如采用PD调节器时。另外，分析高阶系统时可以将其分解为多个一阶和二阶系统，这时的二阶系统往往带有零点。所以研究零点对二阶系统响应性能的影响具有重要意义。

几乎所有该类课程的教材都会讨论二阶系统(没有零点)的响应性能问题。但是，对于零点的影响以及配置原则尚未全面深入的分析结果。有的教材基本上不讨论零点问题，有的主要分析开环零点对闭环特征方程的影响，还有的则只通过仿真例子简单说明一下零点对暂态性能的影响。例如，文献［1］只笼统地指出增加零点相当于增加了一个微分分量，作用是使响应加快、超调量增大、振荡加剧、调节时间拉长;文献［2，3］针对比例微分调节器给系统带来的零点，给出了阻尼比在0～1之间时性能指标的一些计算公式;文献［4，5］仅通过仿真分别分析了二阶和三阶系统的开环零点对暂态性能的影响;文献［6］讨论了独立改变系统零点的作用，但也限于阻尼比在0～1之间的情况，且分析仅基于计算结果，没有全面的定性分析。

实际上，零点对二阶系统的影响比较复杂。有时会加快响应，有时正好相反;有时会在加快响应的同时增大超调，有时却可以不产生超调而只加快响应;有时会使振荡加剧，有时却完全不产生振荡。那么，到底什么情况下零点的存在会改善性能?什么情况下会使性能恶化?配置零点应遵循的基本原则是什么?本文针对这些问题进行定性和定量的全面分析，并给出清晰的答案。

1 有零点二阶系统响应的基本特征

设系统的输入和输出分别为R(s)和Y(s)，则有零点二阶系统的传递函数可以表达为

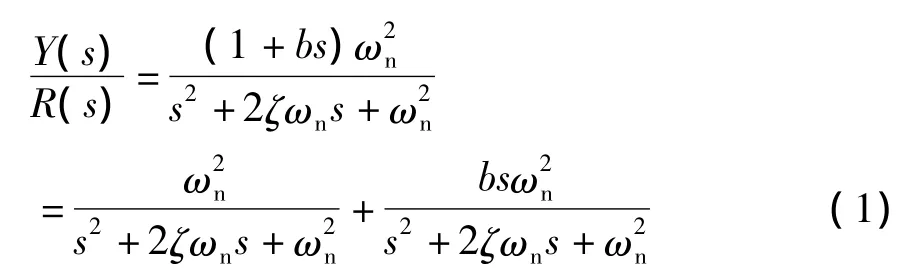
可见系统输出为无零点典型二阶系统响应及其微分部分两项的叠加：

式中，y0(t)为无零点典型二阶系统的响应。因此，零点的影响体现为增加了一个微分项，而且零点越靠近原点，|b|越大，影响越显著。

以下分析针对单位阶跃输入，并设系统稳定，即阻尼比ζ与自然振荡频率ω0均大于零。分实数极点与复数极点两种情况进行讨论，每一种情况都要考虑b＞0与b＜0，即负实数零点与正实数零点对系统动态响应性能的影响。

2 实数极点时零点对性能的影响

2.1 b﹥0，系统零点为负实数

先考察一个仿真例：

b取0.5和1.5不同值时系统各部分的单位阶跃响应曲线如图1所示。图1表明，系统极点为负实数时，由于无零点的响应y0(t)是单调上升的，所以其微分始终大于零。当b较小时，如图1(a)所示，总的输出y(t)不会产生超调，且响应加快;但当b较大时，如图1(b)所示，由于叠加的微分项过大，会导致y(t)产生超调。因此，需要搞清楚一个重要问题：定量地分析，b到底增大到什么值时才会产生超调?

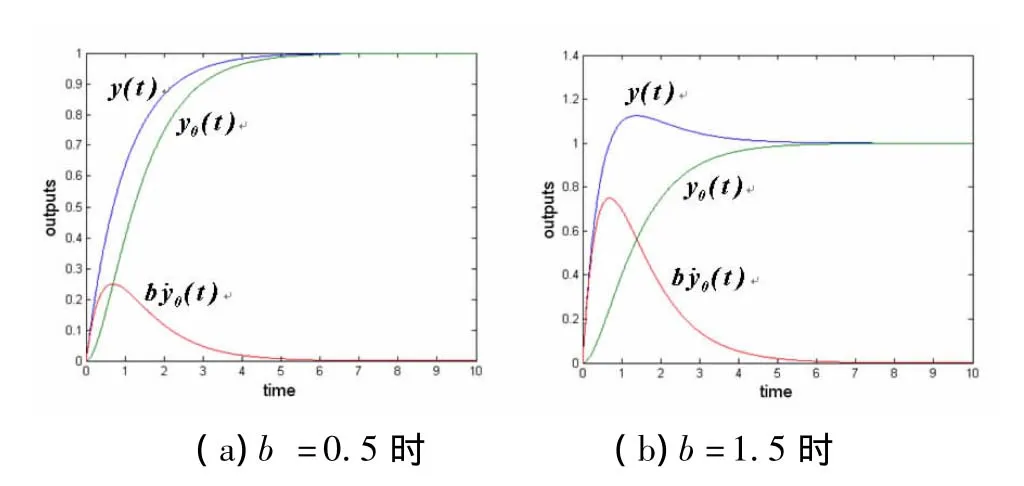
图1 单位阶跃响应曲线

分析的主要思路是若产生了超调，则响应有峰值，在0＜t＜∞的范围内一定存在一时间点t1，使得(t1)=0。

先考虑ζ＞1，即系统的两个极点s1和s2互异，并设s1＞s2。系统无零点部分的单位阶跃响应为

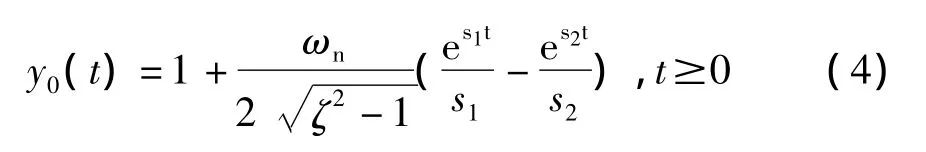
加上微分项后可得到总的响应，再求导可得

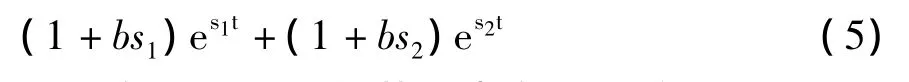
因此在0＜t＜∞的范围内有如下关系

上式左端是极点s1和s2与零点-1/b的距离之比，说明只有当零点位于负实轴上极点s1的右端时(见图2)，式(6)才成立。即此时一定存在某时间点t1＞0，使系统响应的导数=0，系统响应出现峰值和超调。

图2 系统零极点分布示意图

再考虑ζ=1，即系统的两个极点s1和s2相同，即s1，2=－ωn。系统无零点部分的单位阶跃响应为

与前面同样的思路，对总的响应求导后可得t+b－bωnt=0，即

上式左端的分母代表了极点与零点的距离，同样说明只有当零点-1/b位于两个极点s1，2=-ωn的右端时，才存在某时间点t1＞0，使系统响应的导数等于0。

上述分析说明无论系统极点相同或互异，只有当零点比极点更靠近原点时才会产生超调。式(6)和式(8)同时还表明，b越大，则零点越靠近原点，系统产生峰值的时间点会越提前。而且，由式(2)知对应的微分项越大，超调也会越大。

为了进一步验证上述结论，我们针对式(3)所代表的相异极点系统和下式所代表的相同极点系统进行仿真：

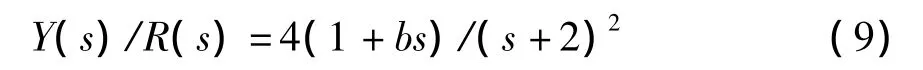
b的取值大致在产生超调前后，仿真结果如图3所示。仿真结果证实了前面分析的结论，即对于具有负实数极点的二阶系统，其负实数零点比极点更靠近原点时一定会产生超调，且零点在极点的右端距极点越远(越靠近原点)，超调就会越大。

图3 b取不同值时的二阶系统单位阶跃响应

2.2 b﹤0，系统零点为正实数

这种情况与前面的区别只是式(2)中构成系统响应的微分项部分的符号正好反过来，因此其作用是显而易见的。我们只须针对前面的式(3)所代表的系统做一组仿真就可看出其响应的一般规律。仿真结果如图4所示，说明当b＜0时，由于式(2)中的微分项始终为负，因此总的响应虽然不产生超调，但会产生反调;随着b的增大，反调也越来越大，而且上升时间和调节时间都会延长。

3 复数极点时零点对性能的影响

我们先考察一个仿真实例：

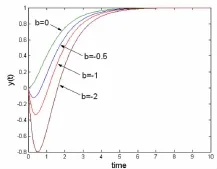
图4 b取不同负值时实数极点系统的单位阶跃响应

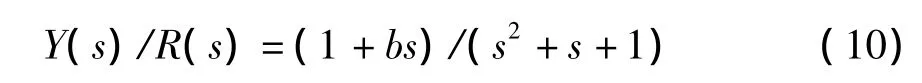
其极点为s1，2=-0.5 ± j0.5，取b±0.5 时系统各部分的单位阶跃响应如图5所示。

图5 二阶系统的单位阶跃响应曲线

由图5可以看出，当系统极点为复数时，由于无零点的响应y0(t)有振荡，所以其微分在y0(t)达到峰值或极值前大于零或小于零，而在y0(t)达到峰值或极值后则正好反过来，所以无论b的取值如何都会加剧振荡幅度，增大超调。在响应的快速性方面，上升时间和峰值时间在b＞0时会减小，而在b＜0时会增大，调节时间对于该例而言变化不大。但是在|b|较大时，由于振荡幅度会显著增大，所以调节时间应当是增加的。

下面针对一般情况先分析峰值时间与超调，然后分析调节时间。

设系统的极点为s1，2= σ ± jωd，其中 σ =-ζωn，，则无零点部分的单位阶跃响应及其微分分别为

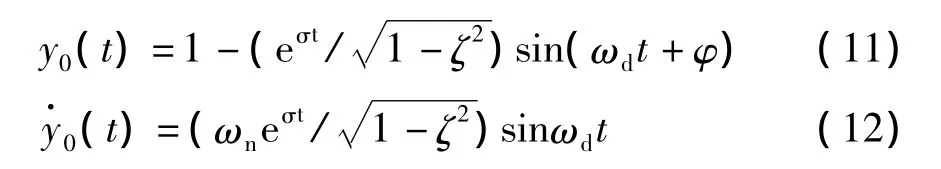
其中，φ=cosζ为阻尼角。将上述两式代入式(2)并对总的输出y(t)求导可得峰值时间tp满足下式

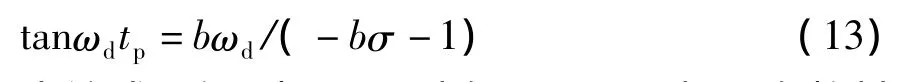
由该式可知：当b=0时有ωdtp=π，与现有教材典型二阶系统的相关结论一致;当b＞0时，则有ωdtp＜π，且ωdtp随b的增大而减小，即峰值时间缩短，b增大到-1/b=σ时有ωdtp=π/2，即零点在实轴上右移到极点实部位置时峰值时间将减小一半，继续增大则tp还会减小，但最多减小到ωdtp＜φ;而当b＜0时，则有ωdtp＞π，且ωdtp随b的减小而增大，但最多增大到π+φ。说明tp的变化受到阻尼角的限制，即+∞ ＞b＞-∞对应φ＜ωdtp＜π+φ。

对于响应峰值和超调，无论tp是减小还是增大，不同b所对应的曲线都相交于y0(t)的峰值点，tp的改变使y0(t)的峰值不再是有零点响应y(t)的峰值，所以y(t)的峰值一定大于y0(t)的峰值。也就是说复数极点情况下，零点的存在会使超调增大，而且由于|b|越大，在y0(t)基础上叠加的微分分量的幅度也越大，因此超调会随之增大。

最后再分析调节时间ts。设误差带为Δ(一般取5%或2%)，则按照其定义可推导出

按包络线估计调节时间可将上式简化为

从而可得

即调节时间比无零点时多出了lna这一项。分析该项可知：b＜0时有a＞1，lna＞0，因此ts一定会增大;而b＞0时有三种情况，即b=2ζ/ωn对应a=1，b＞2ζ/ωn对应a＞1，b＜2ζ/ωn对应a＜1，表明ts可能不变、增大或减小。由于这是按包络线估计的大致结果，与实际情况会有一些出入。

根据该节的分析结果，我们针对式(10)进行仿真，结果如图6所示。该图表明，无论b＞0还是b＜0，随着|b|的增大，即零点-1/b向原点靠近，都会使振荡加剧，超调增大，即平稳性变差;在快速性方面，调节时间在较小时变化不明显，在|b|较大时则明显延长;峰值时间tp会随|b|的增大而减小(b＞0时)或增大(b＜0时);无零点情况下(b=0时)的峰值时间为π/ωd=3.63，当b=2，即零点位于极点实部位置时，tp正好减小了一半，为1.815;由于阻尼角φ=π/3，所以tp最多减小到原来的1/3，即1.21。tp增大的极限则为4.84(即ωdtp→π+φ所对应的时间 3.63+1.21)。

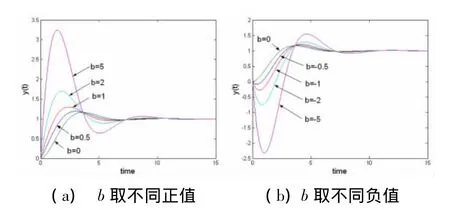
图6 二阶系统的单位阶跃响应

综上所述，对于复数极点的二阶系统，增加零点会使系统响应的振荡加剧，且零点越靠近原点，振荡幅度就越大，即平稳性越差;若零点位于右半复平面，快速性也会下降;若零点位于左半复平面，响应速度虽然会有所提高(上升时间和峰值时间缩短)，但调节时间并没有改善，反而会在零点靠近原点时明显延长。因此，综合评价，增加正实数零点是有害无益，增加负实数零点是弊大于利。在设计系统时，即使无法避免零点，也应当尽可能地使零点位于负实轴上，而且距离原点远一些。

4 结语

本文针对有零点的二阶系统，全面分析了零点对响应性能的影响，讨论了系统分别具有左半复平面实数和复数极点时对应的零点在负实轴和正实轴上四种情况。根据分析结果综合评价：只有当系统具有实数极点时，恰当地配置一个负实数零点可以明显改善快速性，且不影响平稳性，所配置零点的位置尽量不要比极点更靠近虚轴，以避免产生超调;若要追求快速性，可以让零点比极点适当地靠近虚轴一些，这样虽然有超调但不会太大。

［1］黄家英.自动控制原理(第二版，上下册)［M］.北京：高等教育出版社，2010.

［2］胡寿松.自动控制原理(第五版)［M］.北京：科学出版社，2007.

［3］张爱民.自动控制原理［M］.北京：清华大学出版社，2006.

［4］Ogata K.Modern Control Engineering(4th Edition)［M］.北京：清华大学出版社(影印版)，2005.

［5］Kuo B C，Golnaraghi F.Automatic Control Systems(8th Edition)［M］.北京：高等教育出版社(影印本)，2003.

［6］Dorf R C，Bishop R H著，谢卫红，邹逢兴等译.现代控制系统(第八版)［M］.北京：高等教育出版社(影印本)，2001.