自密实混凝土单轴受压应力——应变全曲线试验研究

陈 莉 王海伟 王建华

（江苏省洪泽湖水利工程管理处，江苏 洪泽 223100）

0 引言

混凝土的单轴受压应力-应变曲线方程是混凝土材料最基本的本构关系，又是多轴本构关系模型的基础。在钢筋混凝土结构的非线性分析中，例如：构件的截面刚度、截面极限应力分布、承载力和延性，超静定结构的内力和全过程分析等，它是不可或缺的物理方程，对计算结果的准确性起决定性作用。

本试验采用CSS-WAW-1000DL电液伺服万能压力试验机对自密实混凝土棱柱体试件进行了单轴受压试验,得出自密实混凝土的应力-应变全曲线，推出自密实混凝土单轴受压应力-应变全曲线方程，并对其进行分析。

1 试验概况

（1）试验材料

粉煤灰：华能南京电厂生产的F类Ⅰ级粉煤灰。

水泥：中国水泥厂有限公司生产的海螺牌P.O42.5R水泥。

细骨料：江西赣江生产的中砂，细度模数为2.51。

粗骨料：回容峰家山生产的碎石，粒径为5～19 mm，级配连续。

外加剂：江苏博特新材料有限公司生产的JM-PCA（Ⅰ）型减水剂，减水率最高可达35%以上。

（2）配比设计

自密实混凝土配比设计为水泥∶粉煤灰∶水∶砂∶石∶添加剂=318.8∶212.5∶170 ∶766.2 ∶864 ∶4.8（kg/m3）。

（3）试件制作

自密实混凝土每种配比制作3个试件，试件尺寸为150 mm×150 mm×300 mm的棱柱体。

（4）养护条件

本试验中，制作的所有试块均是在实验室标准养护条件下进行养护，温度为20℃，相对湿度为99%。

（5）试验设备

自密实混凝土棱柱体试件加载系统由YHD-50位移感应器、CSSWAW-1000DL电液伺服万能压力试验机、静态应变仪和计算机等组成，数据直接由DH3818静态应变测试仪采集。

（6）试验方法

要获得稳定的应力-应变全曲线，主要是在曲线的下降段必须控制混凝土试件缓慢地变形和破坏。采用CSS-WAW-1000DL电液伺服万能压力试验机对自密实混凝土棱柱体试件进行加载，上升段采用力控制，按峰值荷载的10%分级加载，接近预估峰值荷载的90%时采用位移控制，下降段的加载速度为0.005 mm/s。当试件最大应变达0.01左右或荷载减小至峰值荷载的10%左右时结束试验。

2 试验结果与分析

自密实混凝土的应力-应变全曲线如图1所示。

图1 自密实混凝土的应力-应变全曲线

自密实混凝土的应力-应变全曲线分为上升段和下降段两部分，二者以峰值点为界；自密实混凝土的破坏过程分为四个阶段：弹性阶段、裂缝稳定扩展阶段、裂缝失稳扩展阶段和破坏阶段，与普通混凝土的破坏过程基本相似。

自密实混凝土棱柱体试件刚开始加载时应力较小（σ≤0.4 fc），应力与应变近似成线性关系。继续加大应力，自密实混凝土的塑性变形和微裂缝稍有发展，应变逐渐加速增长，界面裂缝的长度、宽度随着应力的增长而增大，数量随着应力的增长而增多，应力-应变曲线的斜率渐减，开始不同程度的朝着水平轴弯曲。此时，自密实混凝土的泊松比 νs=ε′/ε=0.184～0.214<0.5，体积应变（εν=ε-2ε′）为压缩，但其变化率随着应力的增大而减小。

当自密实混凝土试块的应力值达到σ=（0.8～0.9）fc时，其应变约为峰值应变的（0.51～0.80）εp，切线泊松比νt=0.5，体积压缩变形达到最大值，不再继续缩小，意味着混凝土内部微裂缝有较大开展，但试件表面的裂缝肉眼尚未可见。此后，混凝土内部出现非稳定裂缝，应变和泊松比很快增长，体积压缩变形开始恢复。不久，应力提高有限，即达峰值点。随着应变继续增大，试件的承载力减小，曲线进入下降段而形成一个尖峰，峰值应力即混凝土的棱柱体抗压强度fc，相应的应变为峰值应变εp。普通混凝土达到峰值时对应的应变约为0.002，本试验中自密实混凝土的峰值应变在0.002～0.003之间，约为0.0022，比普通混凝土的峰值应变略大。

自密实混凝土试块的应力-应变曲线进入下降段不久，试件中部的表面出现第一条可见裂缝，此裂缝细而短，平行于受力方向。继续增大应变，应力的下降速度逐渐增加，横向变形迅速发展，试件上相继出现多条不连续的纵向短裂缝，自密实混凝土试件的承载力下降很快，但在应力-应变曲线的下降段存在一个反弯点，即应力下降速率最大的点。混凝土内骨料和砂浆的界面粘结裂缝，以及砂浆内的裂缝不断地延伸、扩展和相连，沿着试块最薄弱的面形成宏观裂缝，并逐渐地贯穿全截面。本试验中自密实混凝土棱柱体试件应力-应变曲线的反弯点对应的应力值约为峰值应力的 55%～65%，即 σ=（0.55～0.65）fc，相应的应变值在0.002～0.003之间。

当自密实混凝土试块的应力-应变曲线进入下降段的反弯点后，各不连续的裂缝开始相连形成斜向裂缝，斜裂缝进一步发展贯穿整个截面，再增大试件应变，此斜裂缝在正应力和剪应力的搓碾下不断发展加宽，成为一破损带，而试件其他部位上的裂缝一般不再发展。试件上的荷载由斜截面上的摩阻力和残存的粘结力相抵抗，剩余承载力缓慢地下降。即使在更大的应力下，混凝土的残余强度仍未完全丧失。此时，自密实混凝土的残余强度约为峰值应力的 15%～25%，即 σ=（0.15～0.25）fc，比普通混凝土的残余强度σ=（0.2～0.4）fc略小。

由上述分析可见，自密实混凝土的应力-应变全曲线与普通混凝土的应力-应变全曲线基本相似，但各特征点的位置和取值有所变化。因此，在进行自密实混凝土结构设计时要注意利用这个特点。

自密实混凝土棱柱体试件的受压变形和破坏过程，决定了其应力-应变全曲线的形状。用无量纲坐标公式表示自密实混凝土受压应力-应变全曲线（如图2）。

无量纲坐标公式：

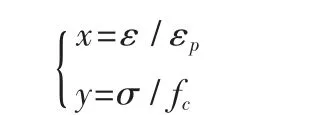
式中:

εp—自密实混凝土的峰值应变；

fc—自密实混凝土的峰值应力，MPa。

图2 无量纲的应力-应变全曲线

由图2可以看出，自密实混凝土的应力-应变全曲线上升段斜率单调下降，在峰值点曲线斜率为零；曲线下降段先出现一个拐点，接着出现曲率最大点，然后曲线趋于平缓，该曲线满足以下几个条件：

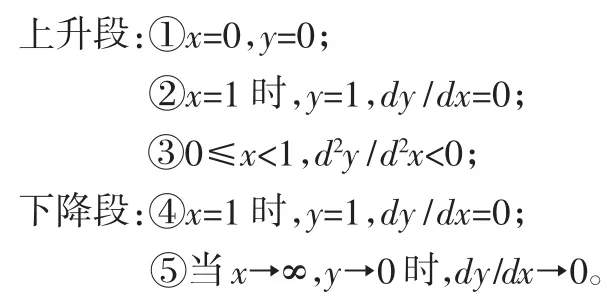
由于混凝土材料的复杂性，要找到一个曲线方程全部满足上述5个条件是比较困难的。在综合和比较前人研究的基础上，建议自密实混凝土应力-应变全曲线方程采用下列形式：

（1）上升段曲线方程

由条件①可得：

式中：

Ec—自密实混凝土的弹性模量，N/mm2；

Es—自密实混凝土的割线模量，N/mm2。

由条件①和②可得：

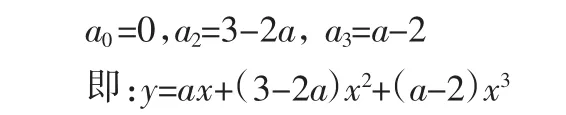
由条件③可得：

d2y/d2x=2（3-2a）+6（a-2）x＜0，得到 a 值的范围：1.5≤a≤3。

（2）下降段曲线方程

由条件④可得：

当 b=0时，y≡1，应力-应变曲线为从峰值点延伸的水平线，相当于理想的塑性变形；

当b→∞时，y≡0，即峰值点之后自密实混凝土的残余强度为0，相当于完全脆性的材料。可知，b值的范围：0＜b＜∞。

条件⑤当 x→∞，y→0时，dy/dx→0，上式满足。

因此，自密实混凝土的应力-应变全曲线方程为：

为了确定自密实混凝土应力-应变全曲线方程中的参数a和b值，进而作出其应力-应变全曲线，将自密实混凝土试件的实测曲线离散化，用最小二乘法进行计算，可得上述应力-应变全曲线方程的参数值，a=2.11，b=1.73。可见，a和 b 值均满足相应的取值范围。本试验提出的自密实混凝土单轴受压应力-应变全曲线方程为：

根据上述方程，可以作出自密实混凝土的计算曲线。图3为自密实混凝土的试验曲线与计算曲线的对比。

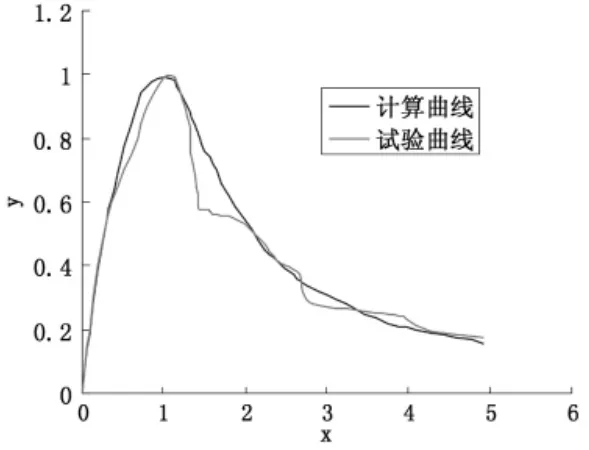
图3 自密实混凝土的试验曲线与计算曲线

通过图3对比可以得出，自密实混凝土的计算曲线与试验曲线吻合良好。因此，试验建议的自密实混凝土单轴受压应力-应变全曲线方程可以很好的描述自密实混凝土的单轴受压应力-应变全曲线。

3 结论

自密实混凝土的应力-应变关系曲线与普通混凝土的应力-应变关系曲线基本相似，但各特征点的位置和取值略有变化。

建议自密实混凝土的应力-应变全曲线方程为：

其中：a值的范围：1.5≤a≤3，b值的范围：0＜b＜∞。

自密实混凝土的计算曲线与试验曲线吻合良好。因此，本试验推出的自密实混凝土单轴受压应力-应变全曲线方程可以很好的描述自密实混凝土的应力-应变全曲线。