适用于宽马赫数的尾喷管优化设计①

陈 兵，谷良贤，龚春林

(西北工业大学 航天学院，西安 710072)

0 引言

高超声速飞行器的后体/尾喷管是高超飞行器一体化的重要部分，是体现气动/推进系统耦合的重要部件。尾喷管既是冲压发动机的主要推进型面，某些条件下其推力可达总推力的70%［1］;同时，也是重要的气动型面，其性能好坏影响整个飞行器的飞行品质。

国内外对高超声速喷管的研究较多，中国空气动力研究与发展中心的周正等通过Rao方法建立SERN模型，并通过优化算法对其进行多目标优化［2］;北航的曹德一等应用特征线法结合遗传算法，提出了一种尾喷管优化设计方法［3］;西工大的李建平等通过最小长度理论和粒子群算法，进行了超燃发动机的尾喷管设计［4］，空军工程大学的文科等考虑了不同进口马赫数对喷管性能的影响［5］，美国空军的怀特实验室在20世纪90年代开发了一套利用响应面法的高超声速喷管的优化设计代码［6］。目前，国内对高超尾喷管优化设计的设计点较单一，对于飞行速域和空域较大的飞行器，单一设计点优化出的喷管构型，很难保证飞行器在整个飞行过程中的性能。此时，尾喷管的设计要考虑其在多个设计点的综合性能。

本文针对高超飞行器的大速域和大空域的飞行特点，进行多点综合优化，通过拉丁方采样，利用CFD手段进行喷管的性能计算，建立响应面，通过遗传算法对喷管进行优化设计，保证喷管能满足宽马赫数范围的推力和升力特性。

1 优化模型

高超尾喷管的优化方法较多，常用的有特征线法、最大推力喷管设计方法、短喷管设计方法等。其设计原则都是保证尾喷管产生的推力尽可能大，对于高超飞行器，基于一体化的考虑，其尾喷管不仅产生推力，同时也是飞行器升力的重要来源。所以，尾喷管的设计要兼顾升力特性。本文采用单壁喷管(SERN)，其型面设计采用三次曲线法，其构型如图1所示。

喷管上表面为三次曲线:

其系数可通过喷管的入口高度H1、出口高度H2、入口扩张角θ1、出口扩张角θ2及喷管总长度L1来确定。以上表面的入口点为坐标原点，则三次曲线的系数为

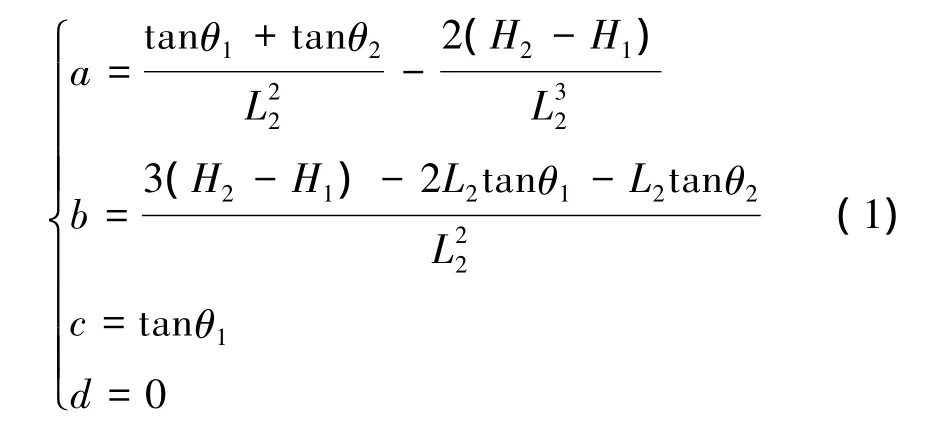
由三次曲线法描述的尾喷管可通 H1、H2、θ1、θ2、L1和L2完全描述，但由于喷管的入口高度受燃烧室出口尺寸的约束，而出口高度又受机身高度的约束。所以，在优化的过程中H1和H2为定值，不作为优化变量。在喷管的设计过程中，最关心的是其产生的推力和升力。所以，具体的优化问题可描述为

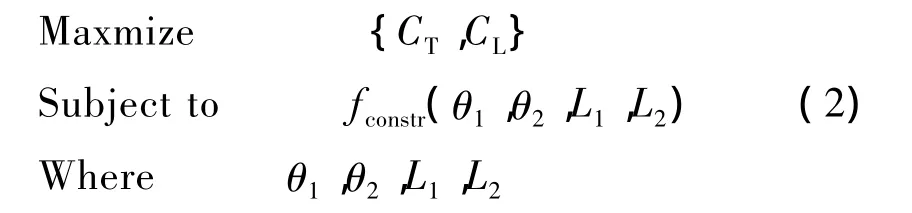
考虑到飞行器尺寸的约束，各优化变量的取值范围为 H1=1，H2=2.4，θ1∈［20°，40°］，θ2∈［0°，15°］，L1∈［1.5，5.0］，L2∈［5.5，6.5］。

为保证尾喷管在整个飞行范围内都有较好的工作性能，其优化采用多点综合优化，分别取来流Ma=2.5、5.0、8.0进行计算，考虑到吸气式飞行器需要在一定的动压范围内飞行。所以，其对应的飞行高度分别取为10、22、30 km。其对应的喷管入口条件如表1所示。

表1 喷管入口状态条件Table 1 Conditions of nozzle intake

2 优化方法

遗传算法是一类随机优化算法，不受搜索空间条件的约束。遗传算法是从代表问题可能潜在解集的一个种群开始，逐代演化产生出越来越好的近似解。其核心思想是模拟生物进化过程中优胜劣汰规则与群体内部染色体信息交换机制，从而处理人工自适应系统中的一系列复杂问题。

遗传算法的求解流程如图2所示。

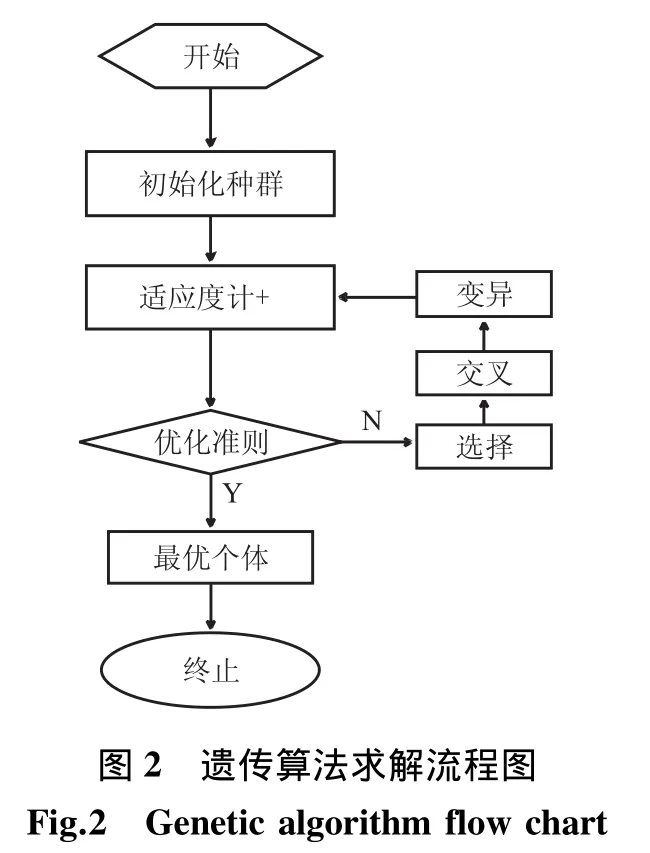
在喷管的优化过程中，通过CFD手段建立推力系数和升力系数的代理模型，通过MatLab自带的遗传算法优化工具箱，可快速准确地优化出在指定优化区域内的目标值，这种方式简单，优化效果好。

3 建立代理模型

3.1 试验设计

常用的试验设计方法包括正交设计、中心复合设计、均匀设计和拉丁方设计等。优化拉丁方由于使用方便、计算代价较小、可靠性高等特点，近年来广泛使用，本文也采用此种试验设计方法。

设有n个变量，每个变量有p个水平，则整个变量空间就分成了pn个子区域。若水平均匀分布，则每个设计变量均分为p个区间。按照以下2个原则进行试验点的选取:(1)样本点在每个子区域随机选取;(2)任一变量在任一维上的投影有p个区间，每个区间有且仅有一个样本点。本文通过拉丁方试验设计方法，选取了20个样本点。

3.2 响应面建立

多项式响应面模型(RSM)是采用多项式回归技术对试验数据进行最小二乘拟合。其中，二阶响应面的基本形式如下:

通过CFD手段，对每个样本点的构型进行计算;通过计算结果，选取其中的15个样本点的计算结果。利用式(3)，建立多项式响应面模型。

对应的响应面如图3所示。

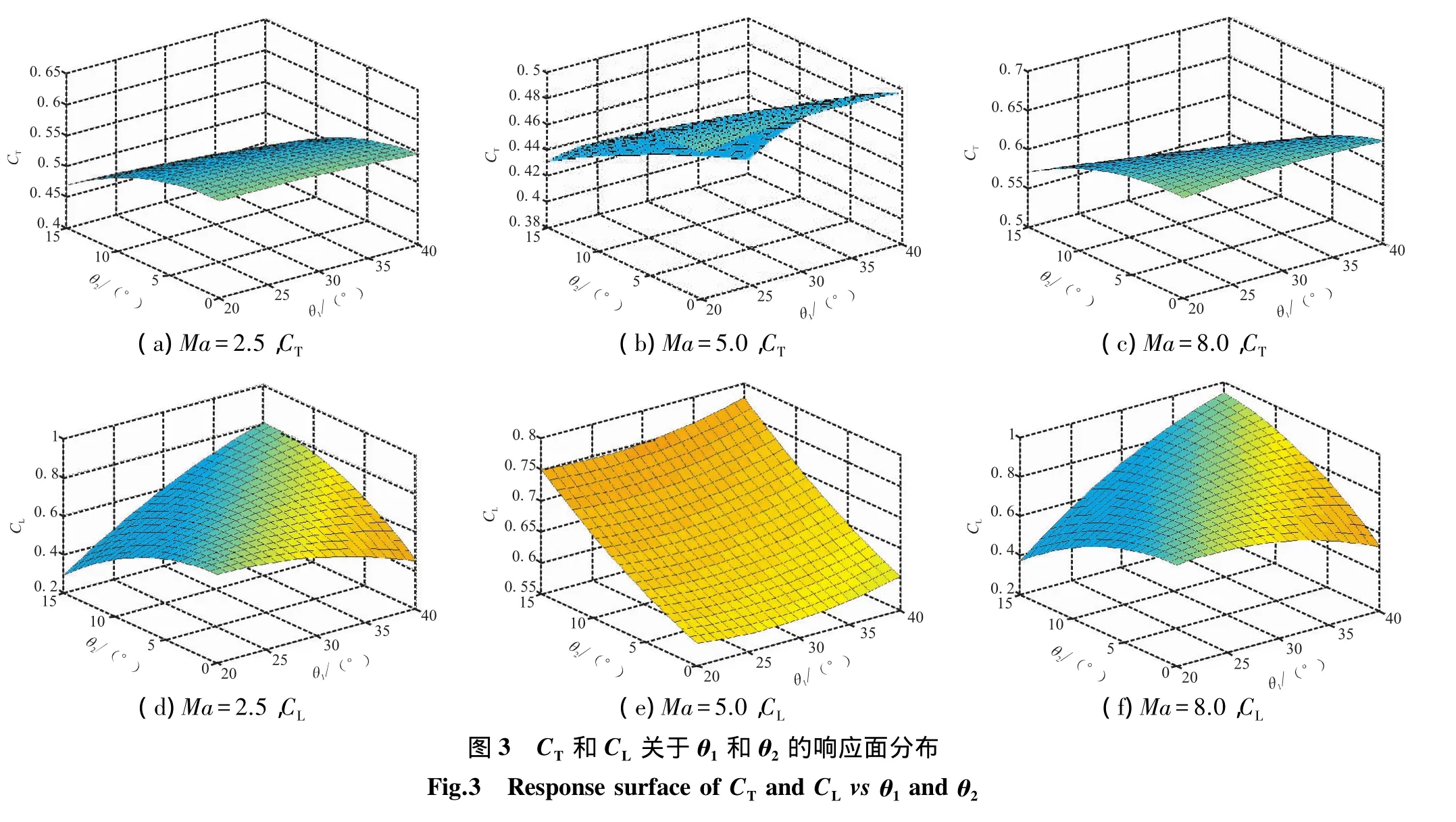
3.3 代理模型检验

代理模型优化方法建立在对真实模型作出近似的基础之上，因此与实际模型之间必然存在误差。通过随机选择3组设计变量，通过数值回代来检验代理模型精度是否满足要求。3组设计变量的θ1/θ2/L1/L2分别为 21.05°/3.16°/3.71/6.45，20°/8.7°/1.5/5.97，24.2°/2.4°/3.5/6.2，数值回代检验结果如表 2 和表 3所示。

表2 代理模型数值回代检验结果(CT)Table 2 Surrogate models’s checkout results(CT)

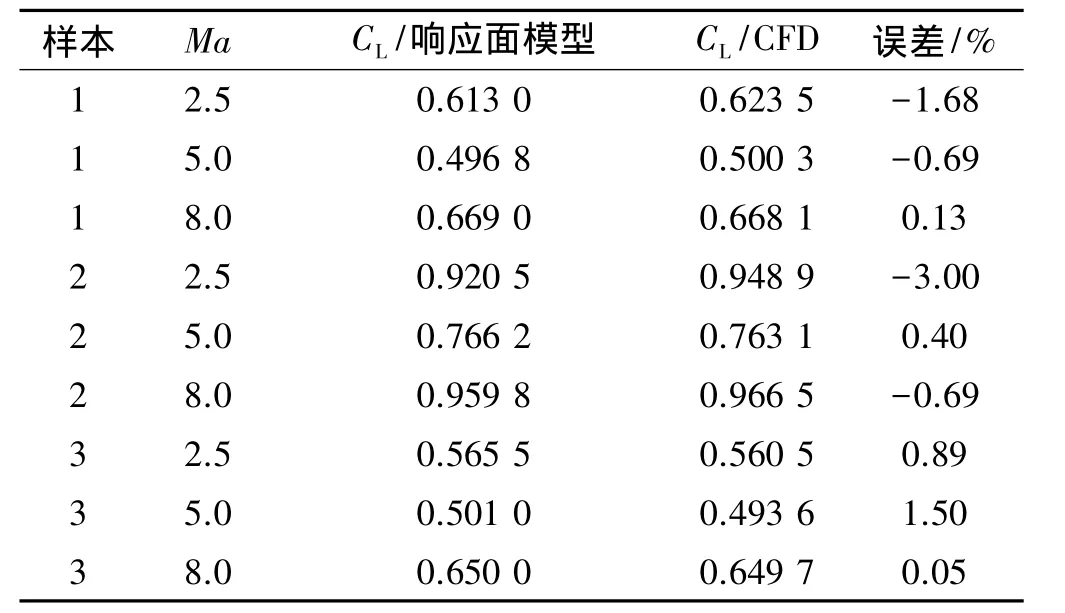
表3 代理模型数值回代检验结果(CL)Table 3 Surrogate models’s checkout results(CL)

通过上述的数值回代计算结果可知，响应面模型建立的代理模型精度满足要求，可用此响应面模型来描述喷管性能。

4 优化结果与分析

本文研究的喷管基准构型为 θ1=25°，θ2=5°，L1=2.5，L2=6。通过CFD计算，得到其性能数据如表4所示。

对于高超声速飞行器，其尾喷管的工作范围较宽，为了保证喷管在整个飞行范围内的性能，需要综合考虑各个状态下喷管产生的升力系数和推力系数。对于在 Ma=2.5、5.0、8.0 条件下，分别以升力系数和推力系数作为目标函数，进行单目标优化。优化结果如表5所示。

表4 基准构型计算结果Table 4 Baseline’s calculation results

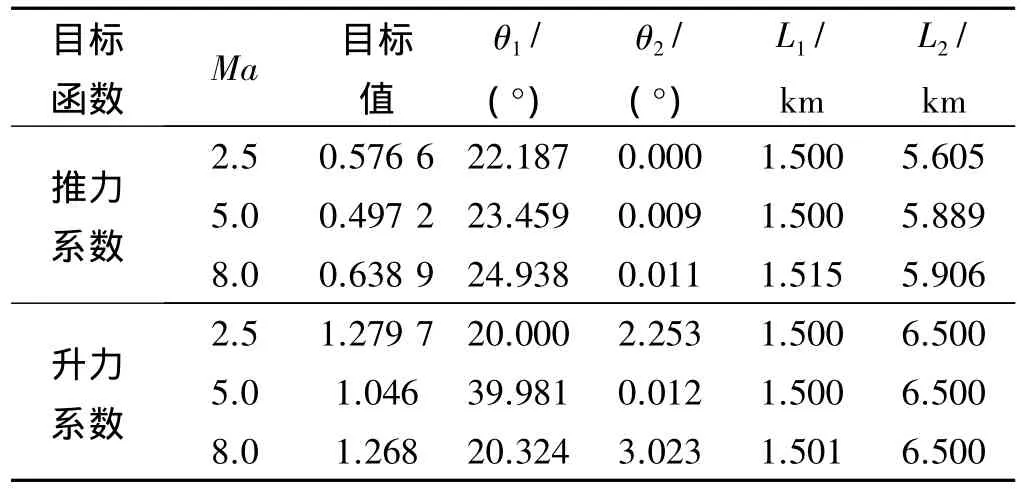
表5 单目标优化结果Table 5 Results of single objective optimization

通过单目标优化，可分别将推力系数提高4.86%、1.46%、1.74%。可见，在现有约束下，通过改变 θ1、θ2、L1、L2对推力系数的提高有限，但能将升力系数分别提高 90.23%、70.12%、64.98%，通过优化，可将升力系数大大提高。

将尾喷管在 Ma=2.5、5.0、8.0 条件下分别进行多目标优化，优化目标函数为升力系数CL和推力系数CT，可得多目标优化的优化前沿如图4所示。

由优化结果的Pareto前沿可知，尾喷管的升力系数和推力系数无法同时达到最优。优化时，需在两者之间进行综合考虑。优化对推力系数的改进有限，但可大大提高喷管的升力系数。在综合优化时，不仅要在升力系数和推力系数之间权衡，也要考虑不同马赫数条件的影响，在最终的优化过程中，可通过加入权值因子来将多点多目标的优化函数转换中，为一个简单的优化函数进行优化。

为保证尾喷管的全速域性能，并考虑推力系数和升力系数对喷管的重要性，通过加入权值因子，对目标函数进行改进，改进的目标函数如式(4)所示。

式中 CL1和CT1分别为Ma=2.5条件下的升力系数和推力系数;CL2和CT2分别为Ma=5.0条件下的升力系数和推力系数;CL3和CT3分别为Ma=8.0条件下的升力系数和推力系数。

以式(4)作为目标函数，利用遗传算法进行优化，最终的优化结果为 θ1=20°、θ1=0.8°、L1=1.5 km、L2=6.5 km，其对应的推力系数和升力系数的计算结果，以及与基准构型计算结果的对比如表6所示。

表6 优化构型计算结果Table 6 Optimum shape’s compute results

优化的目标值为0.669，基准构型的目标值为0.581，优化构型与基准构型相比，目标值提高了15.1%。在高马赫数段，通过牺牲很小一部分的推力性能，可换取升力系数的极大提高。

优化后的构型与基准构型进行对比，如图5所示。

5 结论

(1)单纯依靠改变喷管的入口扩张角、出口扩张角、喷管外罩长度和喷管总长度，对喷管推力性能的影响有限，但其对喷管所产生的升力系数影响很大。

(2)喷管的升力主要由外喷管产生，为得到较大的升力，应保证外喷管长度尽可能长。

(3)喷管优化时，很难保证其推力系数和升力系数同时达到最优值，在多目标优化过程中，需结合实际需求综合分析。

(4)喷管优化时，考虑全速域的影响，通过多点优化出的喷管构型，可很好地适应高超飞行器在整个飞行范围内的需求。

［1］Edwards C L Q，Small W J，Weider J P.Studies of scramjet/airframe integration techniques for hypersonic aircraft［R］.AIAA 75-2581.

［2］周正，倪鸿礼，等.基于Rao方法的二位单壁膨胀喷管优化设计［J］.推进技术，2009，30(4):1011-4055.

［3］曹德一，李椿萱.高超声速飞行器的优化设计［J］.北京航空航天大学学报，2007，33(10):1001-5965.

［4］李建平，宋文艳，李卫强.超燃发动机尾喷管设计方法研究［J］.长春理工大学学报，2007，30(1):1672-9870.

［5］文科，李旭昌，等.不同入口马赫数对超燃冲压发动机尾喷管的性能影响研究［J］.火箭推进，2011，37(3):1632-9374.

［6］Ralph Tolle.A new optimum design code for hypersonic nozzles，utilizing response surface methodology［R］.AIAA 97-0519.