温度影响下炭纤维/环氧树脂复合材料性能预示①

樊 钰，叶定友，，陈汝训

(1.第二炮兵工程大学，西安710025;2.中国航天科技集团公司四院，西安 710025)

0 引言

航天技术的发展对材料在温度影响下的力学性能提出了很高要求。在某些情况下，研究材料的耐温性能，正确地评价材料，使其能满足服役要求，成为航天技术发展和材料科学研究的重要任务。

目前，炭纤维/环氧树脂复合材料以其优异的热力学性能，成为现代固体火箭发动机壳体的首选材料。国内外学者对复合材料在高低温环境下的细观和宏观力学性能开展了系统的实验研究［1－4］，实验结果为建立典型微结构特征和宏观力学性能的定量关系提供了验证数据。但炭纤维/环氧树脂复合材料的内部微观结构非常复杂，有限的实验数据还难以建立起微结构特征和材料性能的全面关系。同时，通过温度力学实验获得复合材料在不同温度下的各种力学性能，需耗费大量的时间以及人力物力，而且只能获得几个温度点下的性能，不能连续测试温度，无法得到完整的材料力学性能随温度变化规律。自20世纪80年代以来，国内外对炭纤维/环氧树脂复合材料在温度影响下的性能预测研究做了一定的工作［5－9］，但多数仅侧重于某个方面的力学参数，缺乏系统性和普适性，尤其是针对固体火箭发动机壳体所用的炭纤维/环氧树脂复合材料，更没有在其高低温宽温度范围内进行过系统、完整的力学性能预示。

本文结合热弹性力学本构关系理论，利用混合定律和Tsai－Hahn准则，建立起基于温度变化的炭纤维/环氧树脂复合材料性能预示模型。梳理并分析宽温度范围内复合材料强度、模量与温度变化的关系，预示该材料的单向力学性能随温度的变化规律，并与实验结果相结合。该预示方法不仅可合理地揭示炭纤维/环氧树脂复合材料复杂的温度变化机理，还可用于评估固体火箭发动机复合材料壳体承受各类载荷的力学行为，极大地减小实验带来的成本及周期问题。

1 理论模型

1.1 理论预示模型的建立

通过对炭纤维/环氧树脂复合材料在温度影响下的力学性能试验，可发现材料力学性能强度及模量均是随温度变化的变量。通过对文献分析，发现对于树脂及其复合材料的单向力学性能随温度变化的规律，可近似地用下式表达:

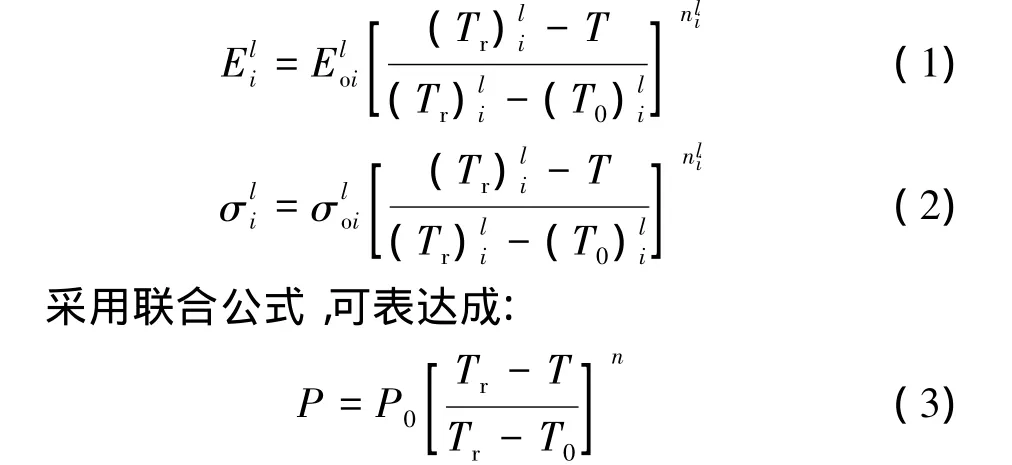
式中 P为材料在某一温度T下的力学性能，如强度、模量等;P0为室温下材料的性能;Tr为参考温度，即材料性能变化可忽略的温度;n为常数;T0和T分别为常温和实际温度。

P0、Tr和n是与温度无关的常数。Tr和n可用最小二乘法求得，且对于固定体系的复合材料是一个常数。因此，若已知Tr和n，便可知该复合材料性能随温度变化的情况。Tr和n曲线可较好地反映树脂的高温性能变化规律，该公式不但适用于树脂体系，也可用于复合材料体系。

综上所述，当已知某类型复合材料的3～4个温度点，就可应用式(3)模型很好地预测材料强度和模量随温度变化的规律。在基体树脂和纤维材料的温度力学性能已知的情况下，可利用“混合定律”和“Tsai－Hahn准则”，预测复合材料力学性能随温度变化的规律。

1.2 对理论模型中常数n的讨论

当温度升高时，即T＞T0时，整个温度变化模型=为小于 1的数。分析可知，当 n0时，;0＜n＜ 说明材料性能随温度没有变化 当1，且随着n的增大，材料性能随温度的变化敏感度减小;当n=1时，材料性能随温度呈线性变化;当n＞1，且n越来越大时，温度对于材料的影响越来越小，可不作为考虑的范围。同时，由实验可知，不论是树脂还是复合材料，随着温度的升高，材料性能均呈现下降趋势。因此，n值不可能出现负数。由以上分析可知，在温度上升的情况下，理论模型式(3)中，n的取值范围是0～1。

当温度降低时，即T＜T0时，整个温度变化模型=为大于1的数。同样分析可知，当n0时，材料性能随温度没有变化;当－1＜n＜0，且随着n的减小，材料性能随温度的变化减小;当0＜n＜1，且随着n的增大，材料性能随温度的变化增加;当n=1时，材料性能呈增加趋势，且随温度呈线性变化;当n＞1且n越来越大时，温度对于材料的影响越来越大。由低温实验可知，不论是树脂还是复合材料，随着温度的降低，材料性能呈现上升、下降及保持不变3种趋势。因此，n值可能呈现正负数形式。由以上分析可知，在温度下降的情况下，理论模型式(3)中，n的取值范围是－1～1。

1.3 对理论模型中材料性能保持率的讨论

将理论模型公式(3)变形得

其中，P/P0是材料性能在某温度T下的保留率，大多数评价则依据性能保留率50%～70%以上的温度作为使用温度。因此，可把从公式中求出性能保留率符合要求的使用温度作为耐温指标。对同一复合材料的不同性能及不同复合材料的同一性能，可进行纵向和横向比较，讨论理论模型公式中的Tr和n:

(1)高温下，固定n，则Tr越大，性能保留率越大，说明材料的耐热性好。如对纵向拉伸模量、强度，Tr趋于无穷大，这性能基本不随温度而改变。

(2)低温下，固定n为正值，则Tr越大，性能保留率越低，耐低温性能差;固定n为负值，则Tr越大，性能保留率越高，耐低温性能好。如Tr趋于无穷大，这性能基本不随温度而改变。

(3)高温下，固定Tr，则n越小，性能保留率越大，说明材料的耐热性好。

(4)低温下，固定Tr，n不论为正值还是负值，随着n值的增大，材料性能保留率越高，即耐低温性能越好。如n=0，则认为该材料性能不随温度而改变;如n=1，则认为该材料的性能保留率与温度呈线性变化。

(5)若Tr和n均不固定，则往往很难比较。这时用程序及图形软件把曲线进行叠加，整个使用温度范围内，性能变化的情况便会一目了然。

2 实验内容

根据固体火箭发动机的研制发展需求，对炭纤维/环氧树脂复合材料力学性能进行了系统的温度实验研究。由于高速飞行导弹在研制、生产、运输、贮存过程中可能遇到各种气候环境因素，同时在飞行过程中，弹体承受气动加热带来的高温、冲刷影响，而发动机与外热防护材料之间的背壁温度可能达到几百摄氏度，发动机壳体必须进行外热防护。基于以上因素，确定影响发动机壳体的温度范围，即低温－40℃至高温200℃。按照试验相关标准，在此基础上开展温度影响下树脂基体材料、复合材料层合板的力学性能实验，见图1和图2。

3 分析与讨论

3.1 环氧树脂材料拟合数据及分析

根据前述的理论模型公式，由试验的有限点可得到从低温到高温范围内连续温度的材料性能曲线，若要求性能达到某一值时，可用此公式求出相应的使用温度;反之，给出使用温度，也可求出此时所能达到的性能保留指标。

首先，对环氧树脂材料进行曲线拟合，采用最小二乘法原理自编程序得到Tr和n，表1是环氧树脂在高温和低温下的拟合参数。从表1可看出，所拟合出的Tr和n满足1.2节中的讨论结果。

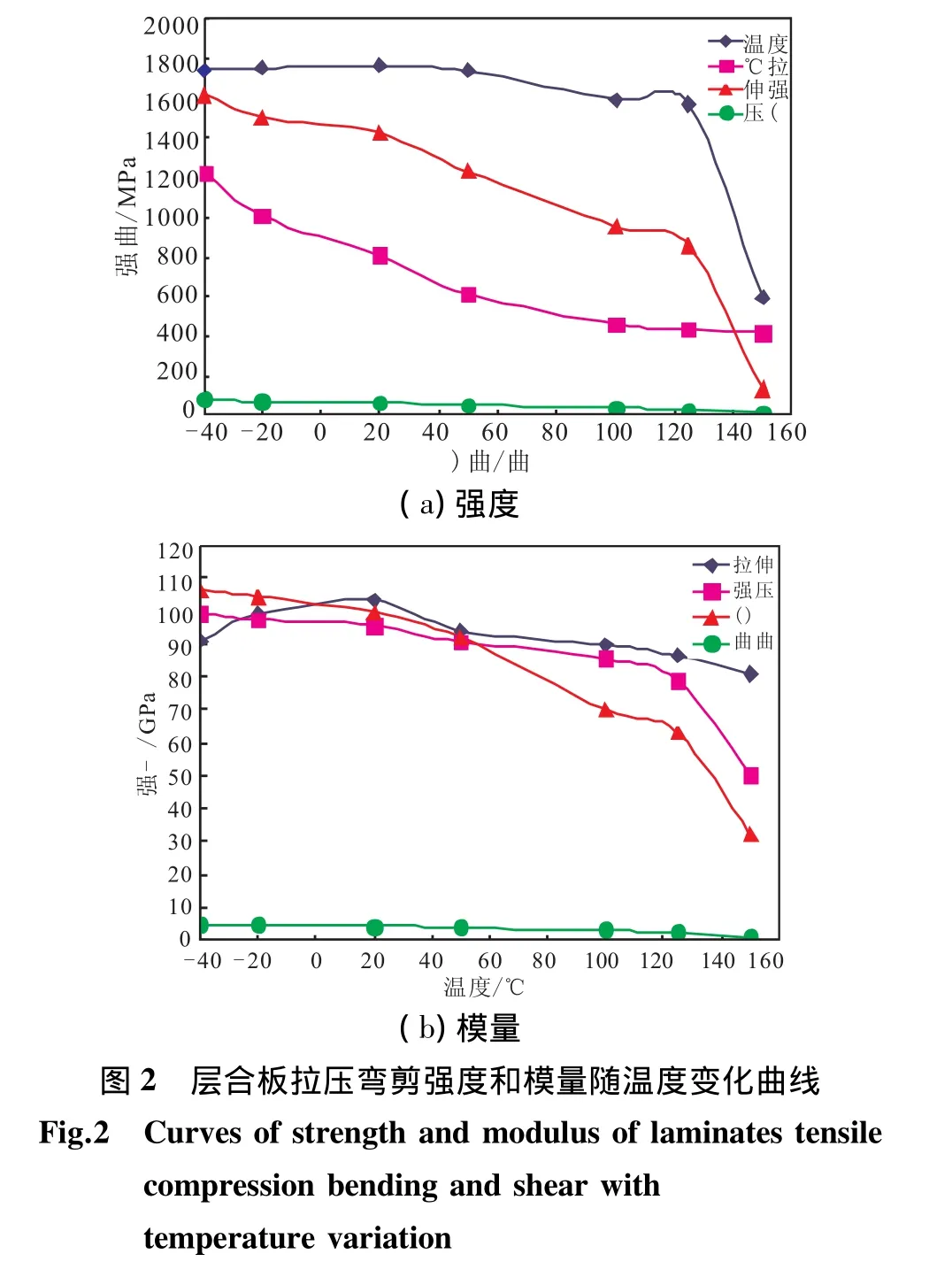
表1 环氧树脂材料Tr和n拟合参数Table 1 Fitting parameters of Trand n of epoxy resin

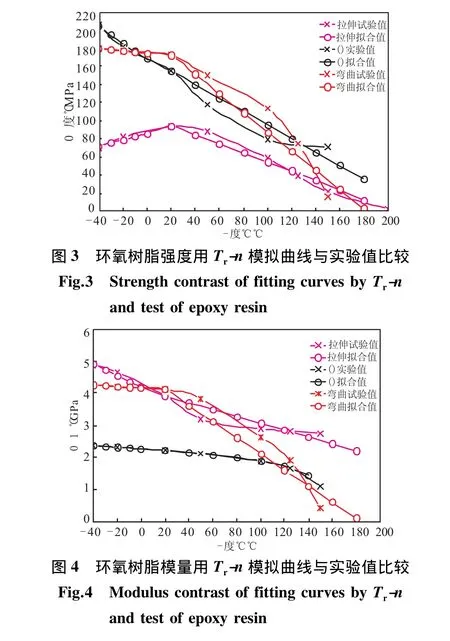
图3和图4分别是环氧树脂材料在－40～200℃之间，拉伸、压缩、弯曲强度和模量用Tr－n模拟出的数据与实际试验值比较结果。从对比图可看出，用所建立的数学模型，通过最小二乘法计算出的数据与试验数据较吻合，能较好地反映出材料在各个温度点下的性能，说明该方法切实可行。

3.2 炭纤维/环氧树脂复合材料拟合数据及分析

针对复合材料随温度变化的性能数据，可用基体在不同温度下的性能及纤维的性能，通过“混合定律”和“Tsai－Hahn准则”来获取。同样应用预示模型(3)，以试验数据为基础拟合Tr和n，获取复合材料随温度变化下的基本力学性能。

表2是炭纤维/环氧树脂复合材料在高低温环境下所拟合出的Tr和n，将拟合曲线与实际实验数据曲线进行对比，两者具有较好的吻合性，见图5和图6。

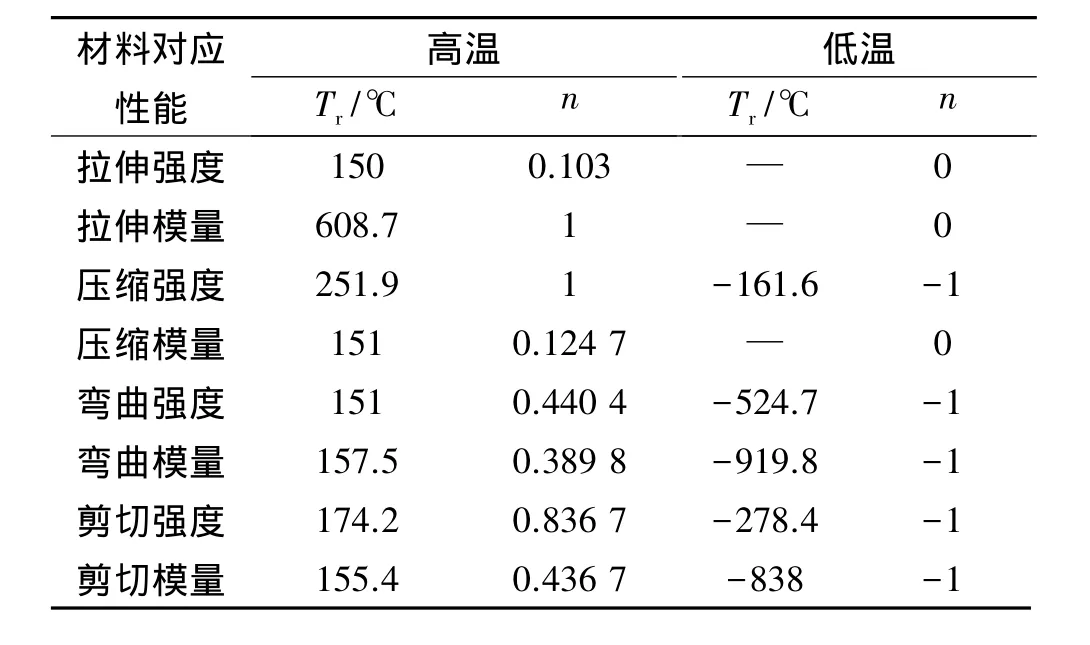
表2 复合材料Tr和n拟合参数Table 2 Fitting parameters of Trand n of composite material

所获得数据对理论预测复合材料的力学性能随温度变化的规律可作为选材的基本依据，对评价和应用复合材料的耐热性有一定的指导意义。

3.3 复合材料容器拟合数据及分析

目前，固体火箭发动机复合材料壳体结构设计是在经典网格理论的基础上，依据工程研制及试验数据，采用系数修正的方法，以适应壳体工作要求为目标推导得出的。该方法是在常温环境下，在常温材料参数的基础上得到的。均衡型缠绕圆筒的爆破压强可近似由式(5)确定:

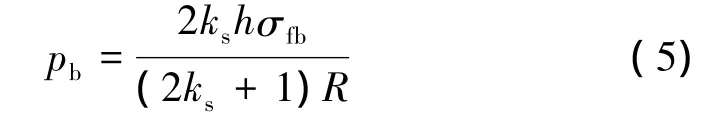
由式(5)可知，h和R均是壳体的结构设计参数，应力平衡系数ks也是与壳体极孔开口大小相关的常系数，以上几个参数均不受温度的影响。因此，在温度影响下，壳体爆破压强只受纤维材料发挥强度的影响。虽然壳体结构设计是基于经典网格理论，不考虑树脂基体的性能，但事实上设计所采用的纤维发挥强度是考虑了树脂基体的影响。同理，通过“混合定律”可知，纤维发挥强度与复合材料、树脂基体的性能相关。因此，均衡型纤维缠绕壳体随温度变化下的爆破压强也可用式(6)表示:

此处，pb0是常温T0下的爆破压强，通过 Tr-n模型，可获得不同温度下壳体的爆破压强。但受实验条件限制，复合材料壳体在高低温下的爆破试数据采集点较少，无法满足最小二乘法理论要求。因此，此处不进行试验数据的拟合对比。

4 结论

(1)提出了炭纤维/环氧树脂复合材料在温度影响下的理论预示模型，分析并讨论了理论预示模型中的相关参数;建立了满足环氧树脂基体材料及炭纤维/环氧树脂复合材料随温度变化的数学模型。

(2)所提出的复合材料受温度影响力学性能预示方法与实验结果吻合较好，能获取材料在任意温度下的性能变化规律，可作为工程应用中材料设计的计算手段和选材基本依据，对评价和应用复合材料耐热性有一定的指导意义。

(3)利用网格理论及混合定律，分析了平衡型纤维缠绕复合材料壳体随温度变化的规律，扩展到对复合材料壳体爆破压强的性能预示。

［1］达道安.空间低温技术［M］.北京:中国宇航出版社，2005.

［2］刘宝锋，李佩兰，黎明，等.5231树脂体系/碳纤维复合材料力学性能研究［J］.高科技纤维与应用，2005，30(6).

［3］李敏，张宝艳.5428/T700复合材料的耐湿热性能［J］.纤维复合材料，2006(1).

［4］Rock A Rushing.High temperature matrices for filament wound composites［R］.AIAA 2005-3613.

［5］Sung K H，Geoge S S.Mechanical properties of graphite epoxy composites at elevated temperature［R］.ICCM-6 ＆ ECCM-2，1987(4):45-48.

［6］Sung K H，Geoge S S.Nonlinear elastic properties of organic matrix composites at elevated temperatures［J］.Transactions of Thesis，1988(10):13-14.

［7］SAMPE.Simulated data for high temperature composite design［C］//International SAMPE Technical Conference，2004.

［8］李芙蓉.先进复合材料耐热性评价［D］.北京航空航天大学，1995:35-45.

［9］刘文博，王荣国，张洪涛.CF/PPEK、CF/PPES复合材料高温力学性能研究［J］.材料科学与工程，2004，12(2):187-188.