AP1000主管道冷段弯管回弹量的理论计算

陈红宇 宋树康 杜军毅

(中国第二重型机械集团公司重型压力容器与核电技术研究所，四川618013)

在管材塑性弯曲变形过程中存在弹性变形。由于回弹量不仅与材料、截面尺寸、弯曲半径、弯曲角度等基本参数有关，也与成型方式、加载路径有关，因此通过塑性弯曲成型理论很难推导出通用的回弹量计算公式。管材弯曲成型时的回弹量往往根据具体的技术条件结合经验来确定。AP1000主管道冷段弯管材料采用316LN超低碳控氮奥氏体不锈钢，外径∅688 mm，内径∅558 mm，弯曲半径2 908 mm，弯曲角度66.6°。由于316LN不锈钢在管材中使用较少而产品尺寸精度要求高，根据成型方法选取合适的工艺参数就显得十分重要。

本文根据316LN超低碳控氮奥氏体不锈钢的材料特性，结合AP1000主管道冷段弯管的尺寸参数，通过理论计算确定冷段弯管弯曲成型时的弯曲力矩、回弹角和半径回弹补偿量，为AP1000主管道冷段弯管成型模具设计提供参考。

1 弯曲力矩的计算

管材在外力矩M作用下弯曲时，变形区内外

侧应力应变状态如图1所示。其中σθ、σD和σt分别代表切向、圆周方向和厚度方向的应力。在外侧区域，σ1=σθ，σ2=σD，σ3=σt；内侧区域，σ1=σt，σ2=σD，σ3=σθ。

图1 管材弯曲变形示意图Figure 1 The schematic diagram of pipe bending deformation

管材弯曲时，其切向应变是绝对值最大的主应变。假定弯曲后变形区的横剖面仍保持为平剖面，则当中性层曲率半径ρ、弯曲角度为α时，距中性层y处的切应变为[1]：

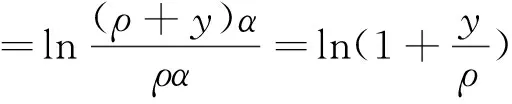
(1)

为便于计算，采用以下基本假设:(1)弯曲过程为纯弯曲，弯曲后变形区横截面仍为平面；(2) 管材周向变形忽略不计，即假定弯曲时管径不变，εD=0；(3)应力中性层和应变中性层重合，位于管材截面中心；(4)塑性变形体积不变，即:εθ+εD+εt=0。

图2是弯曲过程受力分析图。根据力矩平衡原理，管材外加弯矩M的大小应等于其切向应力σθ产生的弯矩之和，故弯曲力矩M为[2]：

(2)

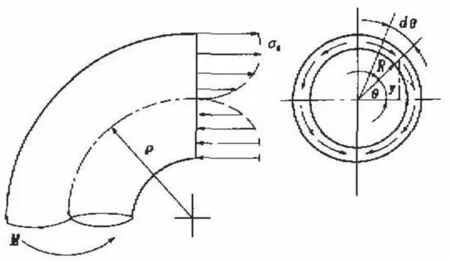
图2 弯曲过程受力分析示意图Figure2 The schematic diagram of forces analysis during bending

AP1000主管道冷段弯管外径∅688 mm，内径∅558 mm，壁厚65 mm，近似作为薄壁管处理，即各纤维间的径向压应力可以忽略不计，σt=0，则应力-应变关系为[3]：

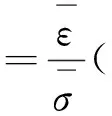
(3)

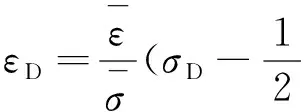
(4)

根据基本假设(2)可以得到；

σθ

(5)

因此，等效应力强度为

σθ

(6)

根据线性强化模型，当ε>σs/E时，具有如下关系[4]：

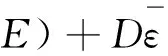
(7)

已知316LN不锈钢的弹性模量E=192 GPa，根据σs、σb可以确定D值，经过整理得：

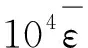
(8)

对于平面应力状态，根据基本假设(4)，εθ=-εt，所以

(9)

将(9)式代入(7)式，则有：

σθ

(10)

将(10)式代入(6)式，则有：

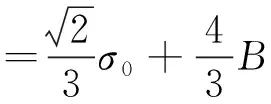
(11)

由(1)、(11)式，则有：

(12)

将(12)式代入(2)式，则有：

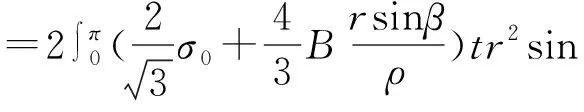
(13)

式中，σ0是补插屈服应力，单位为MPa；t是管材壁厚，单位为m；r是管材内径，单位为m；B是应变刚模量，单位为Pa；ρ是管材中性层弯曲半径，单位为m。

由(8)、(13)式，则有：

≈(6.09×106)N·m

(14)

2 回弹量的计算

假设弯曲后的卸载过程为在塑性弯曲相反方向施加一个假想弹性弯矩M′的过程，则M′=M。

弯管卸载前后中性层长度不变，如图3所示。则有：

αρ=α′ρ′

(15)

式中，α为卸载前弯曲角；ρ为卸载前中性层曲率半径；α′为回弹后弯曲角，α′=66.6°；ρ′为回弹后中性层曲率半径，ρ′=2 908 mm。

图3 管材弯曲回弹示意图Figure 3 The schematic diagram for spring-back of pipe bending

回弹角Δα为：

(16)

图4为管材加载、卸载过程。从图4可以看出[5]：

ε=εe+εp

(17)

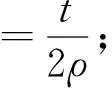
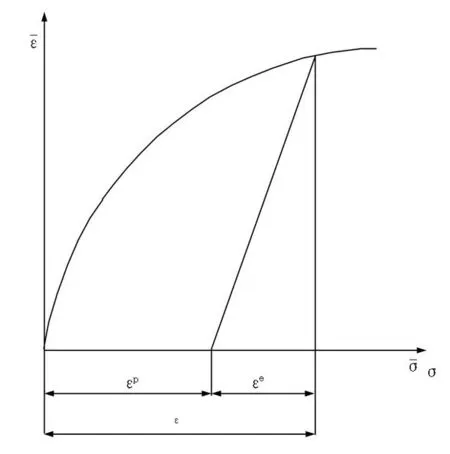
图4 加载、卸载过程Figure 4 Loading and unloading processes

将ε、εe和εp代入(17)式，则有：

(18)

根据AP1000主管道冷段弯管外径、内径和壁厚，得到如下结果：

卸载前中性层曲率半径的计算：

ρ=2.866 m

回弹角Δα的计算：

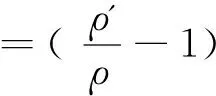
回弹补偿量的计算：

Δr=ρ′-ρ=42 mm

3 结论

通过塑性弯曲理论计算确定AP1000主管道冷段弯管纯弯曲时的弯曲力矩、回弹角和半径回弹补偿量。弯曲力矩M=6.09×106N·m，回弹角Δα=0.98°，半径回弹补偿量Δr=42 mm。

[1] 王珍，邓克，田福祥. 管材弯曲力矩的计算方法. 青岛建筑工程学院学报，2002(1)：87-90.

[2] 王同海.管材塑性加工技术.北京：机械工业出版社，1998.

[3] 汪大年.金属塑性成形原理(第二版).北京：机械工业出版社，1986.

[4] 鄂大辛，宁汝新，古涛. 管材弯曲过程中的弹塑性变形分析. 兵工学报，2009(10)：1353-1356.

[5] 张立玲. 管材塑性弯曲回弹量计算.锻压技术，2002(3)：37-39.