动叶安装角异常反向偏离对轴流风机性能的影响

叶学民， 李春曦， 尹 攀

（华北电力大学 电站设备状态监测与控制教育部重点实验室，保定071003）

动叶可调轴流风机作为一种通用流体机械广泛应用于电力、冶金、石化、煤炭和矿山等领域.该风机的动叶调节系统允许连续调整转子的动叶角度以满足不同工况下的风量需求，具有很高的调节效率.但部分风机的工作环境非常恶劣，如输送含有粉尘的两相介质，因粉尘颗粒进入调节结构引发卡涩，从而导致风机动叶调节异常［1］.另外，由于动叶调节机构精密，动叶的安装质量也是导致叶片出现非同步调节的重要原因之一［2］.

对于此类大型回转机械，现场不仅难以获取动叶异常偏转时的有效数据，而且更难捕获风机的内流特征及其细节.近年来，数值模拟方法给叶轮机械的研究提供了契机［3］.目前，对轴流风机的研究多集中在大型轴流风机的失速与喘振现象［2，4］、叶顶间隙处的泄漏流动和泄漏涡特征［5－7］以及低速轴流风机的前缘滞流区特征和后缘尾迹特征［8］.对其噪声的研究则主要关注叶顶间隙产生的漩涡与噪声间的关系［9］、变工况下叶尖间隙诱发的噪声特征［10］及叶片非等间距周向布置时的降噪机理［11］等方面.而对于动叶异常对轴流风机性能造成的影响，仅叶学民等［12－14］模拟分析了动叶安装角小角度异常、多叶片相邻和相间时的风机内流特征和运行性能的变化.

在动叶调节过程中，异常动叶偏转方向与正常调整方向相反（即动叶安装角出现反向偏离）也是动叶异常偏转的现象之一，这会导致轴流风机出力不足，甚至引发喘振和失速等更大危害.然而，对于两异常叶片反向偏离时，异常叶片安装角偏离度和异常叶片间的相位关系对风机性能的影响尚未有文献进行报道.笔者以OB－84型动叶可调轴流风机为例，通过研究两异常叶片反向偏离情形下的风机性能曲线及特征截面上的总压、熵产率和噪声分布变化，探讨异常叶片安装角偏离度和相位关系对风机性能的影响.

1 数值计算方法

1.1 几何模型

以OB－84型动叶可调轴流风机为研究对象［15］（见图1），该风机转速为1 200r／min，动叶外径为1 500mm，叶片数为14，采用NACA翼型叶片；导叶数为15，动叶与导叶沿周向均匀分布，风机轮毂比为0.6，叶顶间隙为5mm.

1.2 数学模型

风机整体采用非结构化网格（图1），对叶顶间隙处进行网格加密处理.模拟中，分别对网格数为1 96万、246万和312万等情况的模拟结果与原性能曲线进行了比较.结果表明，当网格数为246万时，模拟范围内风机全压和效率的平均偏差分别为1.44%和5.0%，可满足流场细节分析的要求，且有效缩短了计算时间.因此，笔者所进行的模拟计算选用246万网格数，其中动叶区和导叶区的网格数分别为91万和48万.

控制方程组采用带旋流修正的Realizable k－ε湍流模型，该模型适用于旋转流动、强逆压梯度的边界层流动、流动分离和二次流等情形［12－14］.以集流器进口截面和扩压器出口截面作为模拟区域的进、出口，进口边界条件为速度进口，出口边界条件为自由出流.

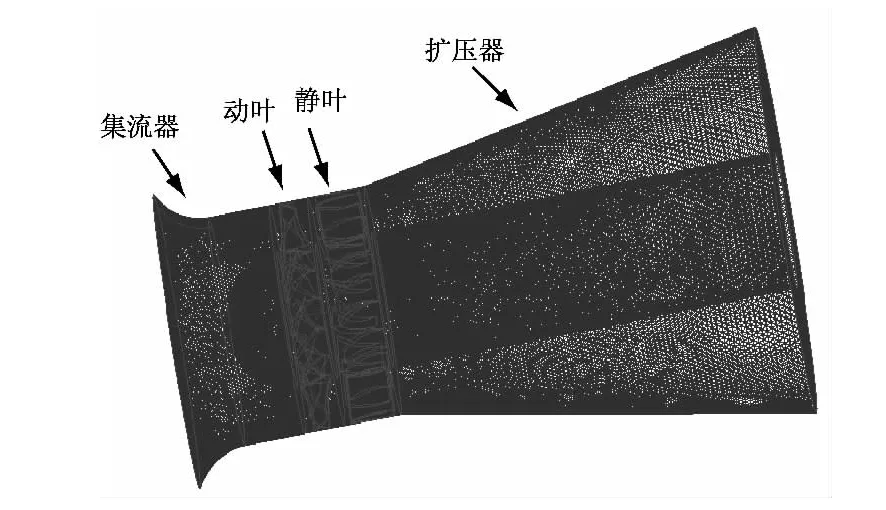
图1 轴流风机结构及计算域网格Fig.1 Structural diagram and grid division of the axial fan

1.3 熵产率计算模型

为考察叶片异常时引起的流动损失变化，采用熵产率分布特征来进行分析.风机内单位体积的熵产率包括黏性耗散引起的熵产率sVD和湍流耗散引起的熵产率sTD［16］：

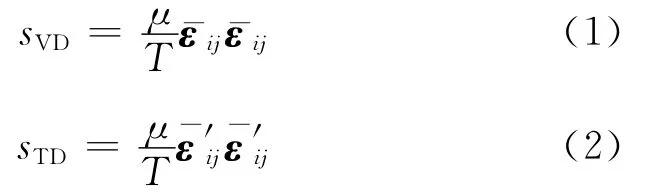
式中：εij和ε′ij分别为平均流场和脉动流场的变形率张量；μ和T分别为流体的动力黏度和温度；“－”表示时均值.

因sTD含有速度脉动项而无法直接计算得到，此处采用Kock等［17］的简化计算模型：

式中：ε为湍流耗散率，m2／s3；ρ为流体密度，kg／m3.

2 计算结果及分析

为分析两异常动叶的安装角偏离度和所处相位变化对风机性能的影响，选取两异常动叶的相位关系如图2所示，其中相位关系分为相间（1号和2号，1号和3号）和相对（1号和4号）等3种情形.安装角偏离度Δβ选10°、20°和30°，当Δβ＝0°时表示叶片安装角处于正常状态.取动叶区出口截面上的总压分布、中间截面上的熵产率和噪声分布来分析风机周向截面上内流特征的变化.

图2 异常动叶间的相位示意图Fig.2 Schematic diagram of phases between abnormal blades

2.1 运行性能和内流特征的变化

2.1.1 运行性能曲线

图3和图4分别给出了两动叶异常时对风机运行性能的影响.由图3和图4可知，两动叶异常时的全压（p）和效率（η）曲线严重偏离正常值，并且随Δβ的增大，风机全压和效率均大幅下降，因此，风机性能更加恶化.且两异常叶片间的相位影响在不同Δβ下也有所不同.

由图3（a）和图4（a）可知，当Δβ＝10°时，全压维持在2 000Pa以下，异常叶片间的相位变化对全压和效率的影响程度基本相同，异常叶片为1号和2号时的影响最大，为1号和3号时的影响最小.与原性能曲线相比，最高效率点由设计流量系数φ＝0.223移至大流量区φ＝0.24，且随流量的增大，效率降幅更大.由图3（b）和图4（b）可知，当Δβ＝20°时，风机全压和效率进一步降低.此时，2种相间关系的影响大体类似，但1号和2号相位关系的影响较弱，而异常叶片为相对关系的影响明显高于相间关系，由此对应的全压和效率值明显低于后者.而受异常叶片影响，最高效率点移至小流量系数φ＝0.21附近.由图3（c）和图4（c）可知，Δβ＝30°时的性能曲线变化与Δβ＝20°时类似，但风机性能显著恶化，此时全压最大值已降低至正常值的50%以下.值得注意的是，当风机处于大流量区φ≥0.25时，异常叶片影响下的风机全压仅为数百帕，且效率低于50%.尤其相对关系的异常叶片在φ＝0.27时，其全压仅为63Pa，效率为3%，此时风机的做功能力几乎丧失，不能起到输送流体的作用.

图3 不同Δβ下异常叶片相位对全压的影响Fig.3 Effects of phase andΔβof abnormal blades on full pressure

图4 不同Δβ下异常叶片相位对效率的影响Fig.4 Effects of phase andΔβof abnormal blades on fan efficiency

为进一步分析异常叶片对风机性能的影响程度，表1给出了在设计流量系数下，与正常状态相比，在异常叶片相位和安装角偏离度Δβ影响下全压和效率的相对变化率.由表1可知，在相同Δβ下，随异常叶片间隔的增大，全压和效率的相对变化率总体呈增大趋势，即风机全压和效率总体降低.这是因为随着异常叶片间隔的增大，单个异常叶片对流场的独立影响逐渐显著，对流场原有周向对称性的破坏逐渐加剧，进一步扩大了异常叶片引起的流场畸变对风机整体流场的影响区域（见下文内流特征分析）；而且，因异常叶片扰动区增大，使得边界层脱离区作用范围扩大，造成脱落的涡流与流道内的主流相互作用区域增大，导致风机全压和效率降低.由此导致对异常叶片附近流道和旋转方向下游流道内流特征的总体影响逐渐加剧，并造成当地流动损失增大，且由表1可知，随着Δβ的增大，该不利影响更为突出.

表1 全压和效率的相对变化率Tab.1 Relative variation of full pressure and efficiency%

2.1.2 总压分布

风机通常在设计工况下运行，因此，针对设计工况分析叶片安装角正常时的风机内流特征，并比较异常叶片相位和Δβ对风机性能的影响.图5为叶片安装角正常时动叶出口截面上的总压分布，由图5可知，总压在周向上总体呈周期性对称分布，而径向上总压的高压区集中在叶高中上部，这也是叶片对气流做功、总压得以提高的主要区域［13，18］.

图5 正常工况下出口截面上的总压分布Fig.5 Total pressure contour on outlet cross section under normal condition

受叶轮旋转影响，在相邻叶片间的流道内也形成明显的高压区.图6～图8给出了相位关系和安装角偏离度Δβ对出口截面总压的影响.由图6～图8可知，异常叶片不仅改变了总压周向分布的对称性，而且不同相位和Δβ下的总压分布形态也明显不同.当Δβ＝10°时（图6），异常叶片为1号和2号、1号和4号时在异常叶片附近出现了相对低压区（总压低于1 400Pa），而叶片异常为1号和3号时则出现多处高压区（总压高于3 400Pa）.因此，相位为1号和3号时对应的风机全压较高，这与图3（a）所得结论一致.

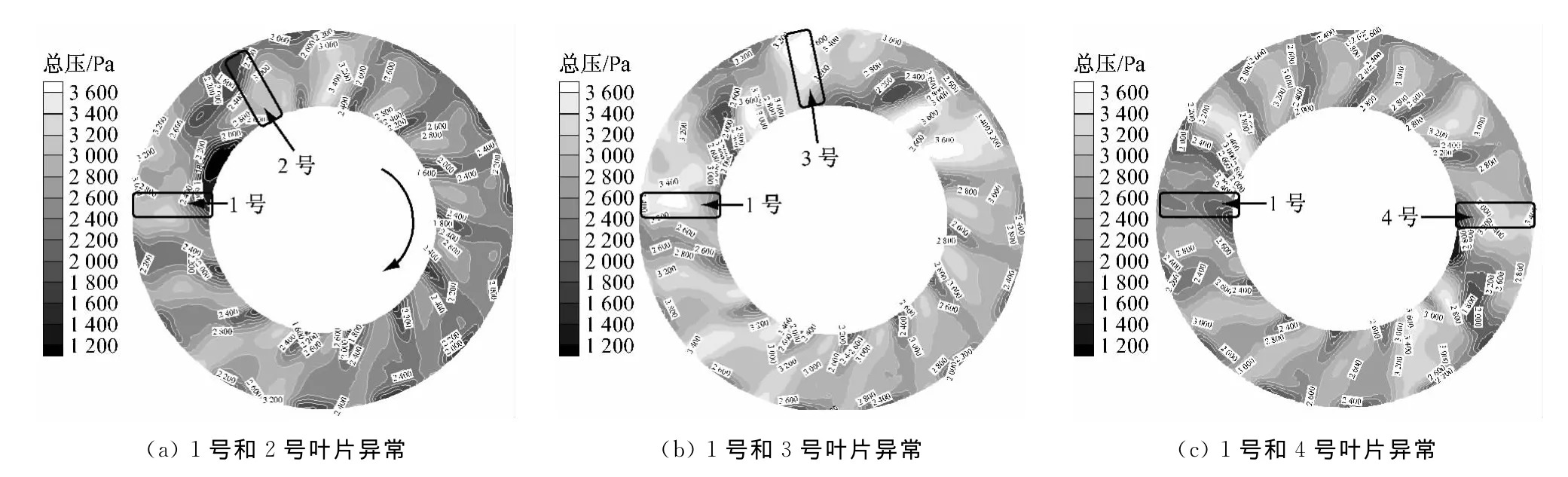
图6 Δβ＝10°时出口截面上的总压分布Fig.6 Total pressure contours on outlet cross section atΔβ＝10°

当Δβ＝20°时（图7），低压区范围进一步扩大.异常叶片为1号和2号时，在叶根区产生带状低压区，沿旋转方向扩展至叶高中部.当异常叶片为1号和3号时，低压范围由叶根区扩大至下游流道的叶顶区，形成覆盖整个流道的低压带.当异常叶片为1号和4号时，形成基本对称的总压分布，其低压区也延续至异常叶片下游流道的叶顶区.对比图7中各图可知，相间异常叶片对内流特征的影响有叠加效应，而相对异常叶片的影响范围有限，因而其总压基本呈对称分布.

当Δβ＝30°时（图8），叶片安装角偏离度进一步增大，且与叶轮旋转方向相同，因而造成内流特征的显著恶化，严重影响风机的整体性能.因此，低压区总压数值进一步降低，范围扩大至覆盖异常叶片下游的多个流道.其中，相对关系时的低压区变化最为显著，影响范围也增大至下游多个流道的大部分区域，这一影响与宏观上风机全压和效率显著降低的结论一致（图3（c）和图4（c））.另外，除异常叶片为1号和3号时的总压分布有局部高压区出现外，其余2种情形对内流特征的影响主要表现为低压区的变化，且周向大部分区域均受异常叶片的影响.

图7 Δβ＝20°时出口截面上的总压分布Fig.7 Total pressure contours on outlet cross section atΔβ＝20°

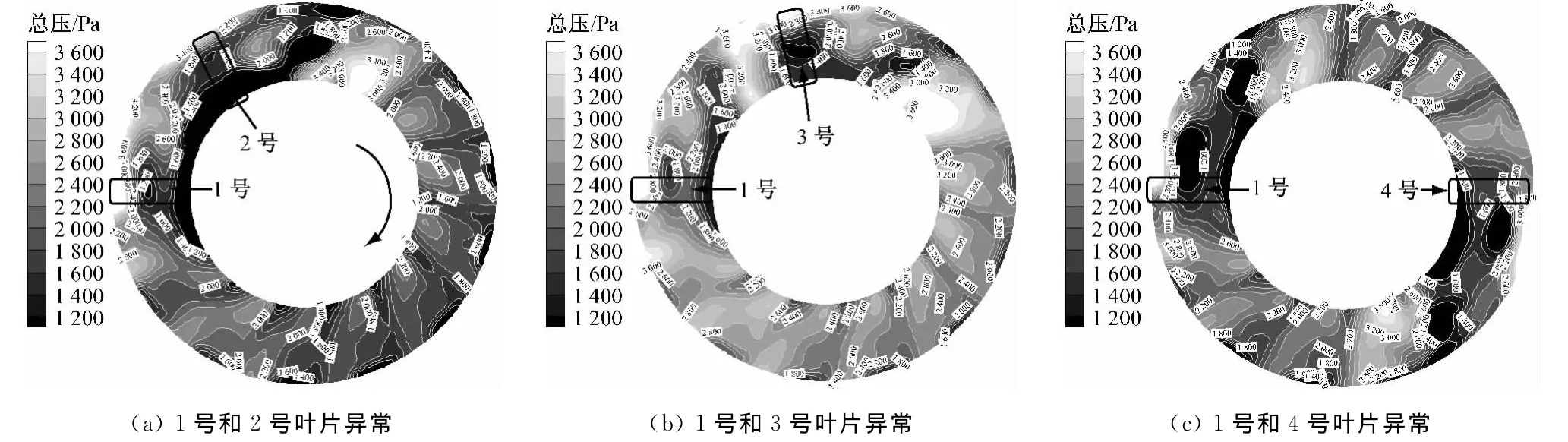
图8 Δβ＝30°时出口截面上的总压分布Fig.8 Total pressure contours on outlet cross section atΔβ＝30°

2.1.3 熵产率分布

熵产率可用于描述流场中能量损失的当地细节特征，从而反映该过程的不可逆程度［16－17］.取动叶区中间截面上的熵产率分布作为其平均变化来研究径向和轴向上的内流损失.图9为设计流量系数下动叶正常时中间截面上的熵产率分布.由图9可知，该情形下的熵产率分布具有极好的周向对称性，且绝大部分区域的熵产率均低于50W／（m3·K），仅在叶片顶部的极小区域存在稍大的熵产率区，这与叶顶存在的泄漏损失有关［4－6，19］.

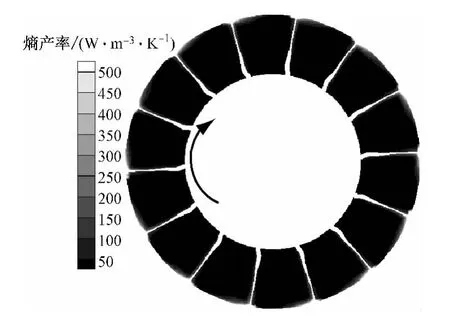
图9 正常工况下中间截面上的熵产率分布Fig.9 Contour of entropy generation rate on middle cross section under normal condition

由总压分布变化可知，因动叶异常导致风机内流特征出现明显紊乱现象，风机内部熵产增加，并导致风机效率降低.图10～图12分别为Δβ＝10°、Δβ＝20°和Δβ＝30°时中间截面上的熵产率分布.当Δβ＝10°时，中间截面上的整体熵产率变化不大，与图9类似，高熵产率区仍集中在叶顶处的狭小区域；其他高熵产率区则零散地分布于异常叶片下游的叶高中部区域，此时风机的内流损失相对较小，这与此时风机效率降低幅度不大的结论一致.

当Δβ＝20°时，高熵产率区大幅增加，且数值明显增大，这与图4（b）中风机效率显著降低的结果相符.因异常叶片反向偏离方向与旋转方向相同，使得进入异常叶片所在流道内的流体被排挤到旋转方向的上游流道，造成上游流道的内流损失增大，因而此处的熵产率较高，并出现覆盖整个流道的高熵产率区，如2号和3号叶片.而且受旋转效应影响，1号和2号异常叶片间耗散和内流损失的叠加作用有所减小，因而2号叶片上游的熵产率有所减小（与图11（b）和图11（c）相比）.随着异常叶片间距的增加，该叠加作用逐渐减弱，异常叶片为1号和4号时，由异常叶片引起的高熵产率区互不干扰，呈对称分布.当Δβ＝30°时，异常叶片附近的内流损失进一步增大，由此造成的高熵产率区在数值和范围上均大幅增大，因而导致风机效率急剧降低（图4（c））.其中，相间关系的异常叶片导致高熵产率区几乎充满了两叶片间的流道和上游流道的大部分区域.

图10 Δβ＝10°时中间截面上的熵产率分布Fig.1 0 Contours of entropy generation rate on middle cross section atΔβ＝10°

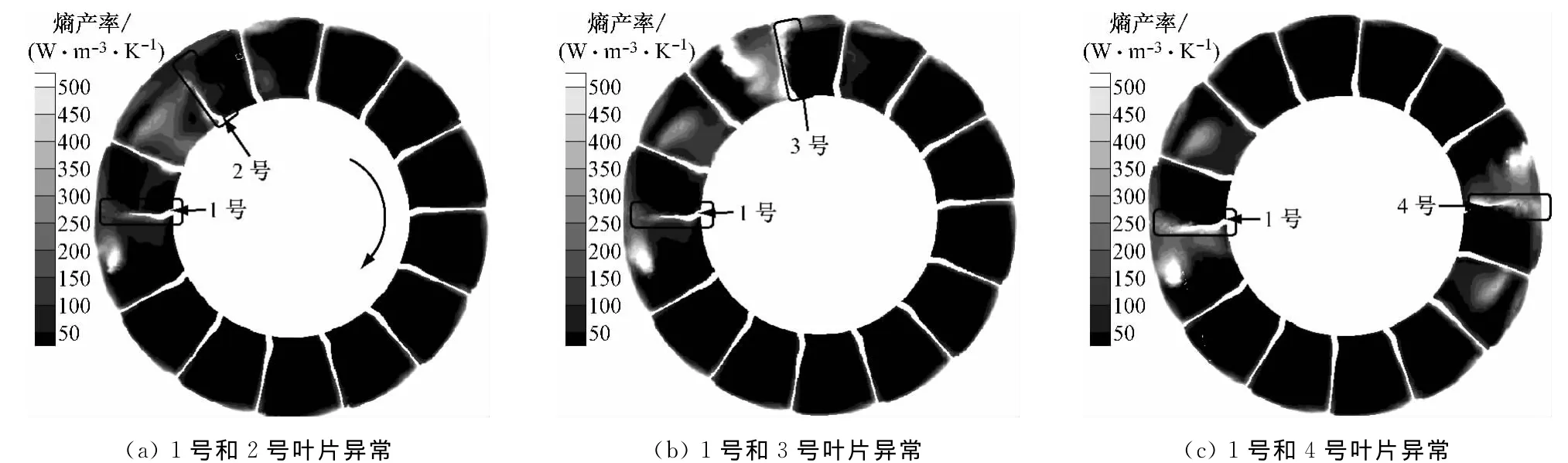
图11 Δβ＝20°时中间截面上的熵产率分布Fig.1 1 Contours of entropy generation rate on middle cross section atΔβ＝20°

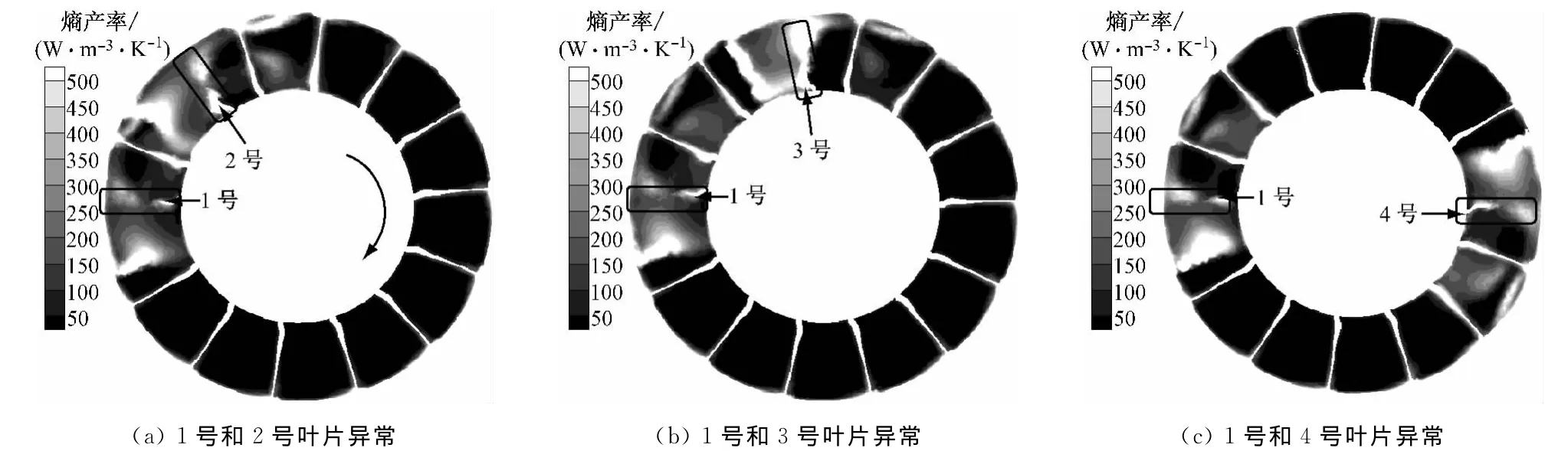
图12 Δβ＝30°时中间截面上的熵产率分布Fig.1 2 Contours of entropy generation rate on middle cross section atΔβ＝30°

2.2 噪声特征

异常叶片的另一重要影响表现为风机噪声的变化，图13为采用Realizable k－ε模型得到的不同情形下的最大声功率级Lw.由图13可知，在正常状态下，风机的Lw随流量系数的增大而增大.当Δβ＝10°时，异常叶片并未改变声功率级的总体变化趋势，但异常叶片导致各流量系数下的Lw整体增大，且异常叶片为1号和2号时的Lw增大幅度最为明显.当Δβ＝20°时，与Δβ＝10°时相比，异常叶片为1号和2号时Lw的变化不大，但另外2种异常工况下Lw变化非常显著，在模拟流量系数范围内Lw保持在145dB的高噪声等级.当Δβ＝30°时，异常叶片为1号和3号时对应的Lw相对较大，3种异常工况下的噪声等级总体处于130～140dB.

图13 不同相位和Δβ下噪声的数值预估Fig.1 3 Numerical prediction of noise at different phases andΔβ

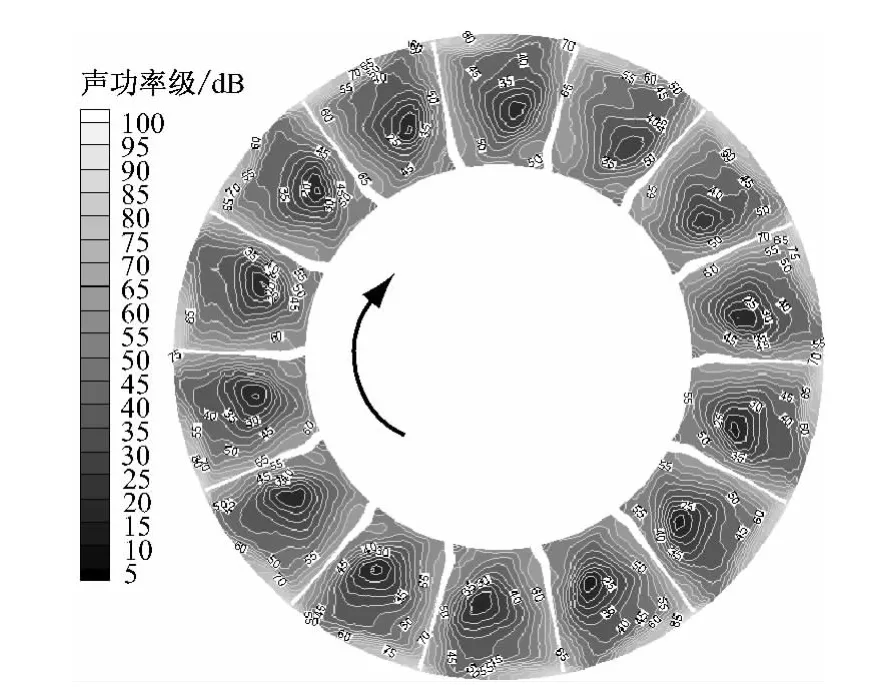
图14 正常工况下中间截面的声功率级分布Fig.1 4 Contour of acoustic source power level on middle cross section under normal condition

图15 Δβ＝10°时中间截面上的声功率级分布Fig.1 5 Contours of acoustic source power level on middle cross section atΔβ＝10°

图14为设计流量系数下动叶区中间截面上的声功率级分布.由图14可知，叶片正常时其声功率级呈周期性对称分布，相邻叶片间的中部存在一显著且范围较大的低噪区，受流体与叶片相互作用及叶片表面上边界层分离的影响，叶片表面附近的噪声高于相邻叶片流道间的噪声，最大噪声源位于叶顶间隙处的微小区域，其值约为90dB，这与叶顶处泄漏损失的影响密切相关［4－6，18－19］.

受叶轮旋转和异常叶片影响，各流道内的气流具有非均匀性，当非均匀气流周期地作用于周围介质时，将产生压力脉动，进而增大噪声.异常叶片对风机声功率级分布的影响见图15～图17.从图15～图17可以看出，随着Δβ的增大，对应的高声功率级区变大.当Δβ＝10°时，异常叶片的总体影响较小，并主要集中在异常叶片附近，此时异常叶片为1号和2号时对噪声的影响较为突出，在两异常叶片间形成1个明显的高噪区，因此其对应的噪声等级较高，这与图13（a）反映的结果一致.

当Δβ＝20°时（图16），中间截面上的整体声功率级的值和范围均进一步增大.其中，相间关系的两异常叶片间产生声功率级达到100dB的高噪声区，而相对关系的异常叶片在其上下游流道均产生明显的高噪声区.当Δβ＝30°时（图17），异常叶片附近达到100dB的高噪声区显著增加，并演变为覆盖上下游多个流道的高噪声带.与内流特征类似，当两异常叶片距离较近时，高噪声区表现出一定的叠加性，而异常叶片为1号和4号时，其影响被限制在上下游流道的有限区域内.

图16 Δβ＝20°时中间截面上的声功率级分布Fig.1 6 Contours of acoustic source power level on middle cross section atΔβ＝20°

图17 Δβ＝30°时中间截面上的声功率级分布Fig.1 7 Contours of acoustic source power level on middle cross section atΔβ＝30°

3 结 论

（1）两动叶异常反向偏离时，风机全压和效率曲线会严重偏离正常值，且随着安装角偏离度Δβ的增大，风机性能显著下降，两异常叶片间的相位影响在不同Δβ下也有所不同.当Δβ＝30°、φ≥0.25时，异常叶片影响下的全压仅为数百帕，效率低于50%.异常叶片使各流量系数下的最大声功率级Lw整体增大，且Δβ＝20°，异常叶片为1号和3号、1号和4号时的噪声增大最为明显，其对应的Lw保持在145dB左右.

（2）异常叶片改变了风机内流特征，不同的异常叶片相位关系和安装角偏离度对特征截面上的总压、熵产率和声功率级分布具有不同的影响.总体上，相间关系的异常叶片对内流特征的影响有叠加效应，相对关系的异常叶片对其附近及下游流场的影响基本对称.随着Δβ的增大，异常叶片的影响逐渐显著，衍生出以范围更大的低压区、高熵产率区和高噪声区为特点的内流特征变化.

［1］王新生.动叶可调轴流风机调整异常原因分析及措施［J］.江西电力，2004，30（5）：27－30，42.WANG Xinsheng.Measure and analysis of abnormal reason on adjusting of moving blade adjusted axialflow fan［J］.Jiangxi Electric Power，2004，30（5）：27－30，42.

［2］马少栋，李春曦，王欢，等.动叶可调轴流风机失速与喘振现象及其预防措施［J］.电力科学与工程，2010，26（7）：37－41.MA Shaodong，LI Chunxi，WANG Huan，et al.Investigation and preventive measures of stall and surge in variable pitch axial fans［J］.Electric Power Science and Engineering，2010，26（7）：37－41.

［3］LI Chunxi，WANG Songling，JIA Yakui.The performance of a centrifugal fan with enlarged impeller［J］.Energy Conversion and Management，2011，52（8／9）：2902－2910.

［4］LIU S H，HUANG R F，LIN C A.Computational and experimental investigations of performance curve of an axial flow fan using downstream flow resistance method［J］.Experimental Thermal and Fluid Science，2010，34（7）：827－837.

［5］TALLMAN J，LAKSHMINARAYANA B.Numerical simulation of tip leakage flows in axial flow turbines，with emphasis on flow physics：part I－effect of tip clearance height［J］.Journal of Turbomachinery，2001，123（2）：314－323.

［6］ZHU Xiaocheng，LIN Wanlai，DU Zhaohui.Experimental and numerical investigation of the flow field in the tip region of an axial ventilation fan［J］.Journal of Fluids Engineering，2005，127（2）：299－307.

［7］LI Yang，LIU Jie，OUYANG Hua，et al.Internal flow mechanism and experimental research of low pressure axial fan with forward－skewed blades［J］.Journal of Hydrodynamics，2008，20（3）：299－305.

［8］ESTEVADEORDAL J， GOGINENI S，COPENHAVER W，et al.Flow field in a low－speed axial fan：a DPIV investigation［J］.Experimental Thermal and Fluid Science，2000，23（1／2）：11－21.

［9］JANG C M，FUKANO T，FURUKAWA M.Effects of the tip clearance on vortical flow and its relation to noise in an axial flow fan［J］.JSME International Journal Series B，2003，46（3）：356－365.

［10］FUKANO T，JANG C M.Tip clearance noise of axial flow fans operating at design and off－design condition［J］.Journal of Sound and Vibration，2004，275（3／4／5）：1027－1050.

［11］CATTANEI A，GHIO R，BONGIOVI A.Reduction of the tonal noise annoyance of axial flow fans by means of optimal blade spacing［J］.Applied Acoustics，2007，68（11／12）：1323－1345.

［12］李春曦，尹攀，叶学民，等.轴流风机动叶异常对风机内熵产影响的数值模拟［J］.动力工程学报，2012，32（12）：947－953.LI Chunxi，YIN Pan，YE Xuemin，et al.Effect of abnormal blade incidence on internal entropy generation in axial－flow fans［J］.Journal of Chinese Society of Power Engineering，2012，32（12）：947－953.

［13］叶学民，李俊，王松岭，等.动叶可调轴流式通风机叶片安装角异常工况下的气动特性［J］.中国电机工程学报，2009，29（26）：79－84.YE Xuemin，LI Jun，WANG Songling，et al.Aerodynamics of adjustable blade axial fan under abnormal installation angles［J］.Proceedings of the CSEE，2009，29（26）：79－84.

［14］叶学民，李俊，李春曦，等.轴流风机多动叶安装角非同步调节下的内流特征和运行特性［J］.中国电机工程学报，2010，30（32）：77－83.YE Xuemin，LI Jun，LI Chunxi，et al.Aerodynamics and operating performance of a variable pitch axial fan with asynchronous regulation of installation angles of multiple blades［J］.Proceedings of the CSEE，2010，30（32）：77－83.

［15］B埃克.通风机［M］.北京：机械工业出版社，1983：361－368.

［16］HERWIG H，KOCK F.Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems［J］.International Journal of Heat ＆ Mass Transfer，2007，43（3）：207－215.

［17］KOCK F，HERWIG H.Local entropy production in turbulent shear flows：a high－Reynolds number model with wall functions［J］.International Journal of Heat＆ Mass Transfer，2004，47（10／11）：2205－2215.

［18］XU Jian，TAN Chunqing，CHEN Haisheng，et al.Influence of tip clearance on performance of a contrarotating fan［J］.Journal of Thermal Science，2009，18（3）：207－214.

［19］POPOV N A，PETROV N.Evaluation of pressure losses in blade rings of axial mine fans and substantiation of their rational design parameters［J］.Journal of Mining Science，2005，41（4）：357－363.