求解0/1背包问题的自适应遗传退火算法

吕学勤，陈树果，林 静

(1.上海电力学院电力与自动化工程学院，上海 200090;2.信阳市供电局财务资产部，河南 信阳 464000)

0 引言

0/1背包问题(zero-one knapsack problem，ZKP)是运筹学中一个典型的NP(non-deterministic polynomia)完全问题［1-2］。背包问题在20世纪50年代末期由Dntzig提出之后，经历几十年的发展，已成功应用于管理科学、计算机科学、分子物理学以及超大规模集成电路设计、代码设计、图像处理、电子工程等领域。目前，解决0/1背包的常规方法包括穷举法、动态规划法和递归回溯法等［3］，但只能处理小规模背包问题。启发式算法是模拟自然界和生物行为的新型算法，具有模型灵活，求解速度快、解的质量高等一系列优点，因而被获得广泛应用。但遗传算法、蚁群算法、差分进化算法等优化算法收敛速度慢、全局收敛性差，而模拟退火算法(simulated annealing algorithm，SA)能改善陷入局部最优解的缺陷，使得算法快速地收敛于全局最优解［4-5］。因此，本文提出了自适应遗传退火算法(adaptive genetic annealing algorithm，AGAA)求解大规模背包问题，通过4个背包问题对算法进行性能对比，结果表明本文提出的算法具有较快的搜索性能和较强的实用价值。

1 背包问题

给定一个可装重量为M的背包及n件物品，物品i的重量和价值分别为wi和ci，i=1，…，n。要选若干件物品装入背包，使其价值之和最大，背包问题的目标函数为

2 遗传算法及其改进

2.1 遗传算法

遗传算法(genetic algorithm，GA)抽象于生物体的进化过程，是一种基于自然选择和群体遗传机理的搜索算法，其本质是一种高效、并行、全局搜索的优化方法。

2.2 遗传算法的改进

GA的改进方案大致有2种:一种是算法本身的编码方式、遗传操作的改进，另一种是GA与其他优化算法构成混合算法。为此，本文把GA与SA相结合构成混合算法，并改进GA交叉、变异方式，使得改进后的算法既保持了GA的高速并行性，又保持了SA跳出局部最优值的能力。

1)编码策略。

针对0/1背包问题，采用二进制编码方案，问题的解可以表示为

(3)式中:fi表示在某一次迭代解空间里的某一个染色体串经适应度评价得到的解;P是由解空间里n个染色体串所得到的解的集合，比如:染色体1为(0，0，1，…，1)，f1=C1× 0+ … +Cn× 1 。

2)选择策略。

为了避免由交叉、变异操作导致破坏最优解或近似最优解的情况，采用轮盘赌和最优保存策略相结合的选择机制，以保留当前最优染色体，即从当前种群中保留2个最佳染色体直接复制到下一代种群中，余下的种群通过轮盘赌方法选择进入下一代种群中，以提高算法的收敛性。

3)交叉、变异策略。

整个遗传进程中，影响遗传算法性能的主要指标为交叉、变异概率，为了维持种群的多样性，交叉概率Pc越大，产生新个体越多，但种群中好的模式被破坏的可能性就越大，即适应度高的个体所占的比重就越少;交叉概率过小时，好的模式保留的可能性越大，种群的多样性难以保证;若变异概率Pm越小，种群中就不易产生新的模式，Pm越大，遗传算法就不满足定向搜索算法的原则，因此，对于实际问题，需多次实验确定交叉、变异概率的取值，而且很难找到适应每个问题的最优解。在自适应遗传算法(a daptive genetic algorithm，AGA)中，Pc和 Pm按(4)式和(5)式进行自适应调整。

(4)—(5)式中:f为当前个体的适应度;f1为当代种群两个个体的较大适应度;favg为当代各个体的平均适应度;fmax为各个体的最大适应度。根据前人经验，(4)—(5)式中 Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.001。

从(4)—(5)式看出，种群中各个体的适应度值接近于局部最优时，Pc，Pm相应增加;种群中各个体的适应度值趋于分散时，Pc，Pm相应地减少。同时，当适应度值高于种群的平均适应度值的个体，对应较低的Pc，Pm，使得适应度高的个体进入下一代种群中;而适应度值低的个体，Pc，Pm会相应地增加，致使该个体被破坏。因此，Pc，Pm的自适应调整能提供个体最适合的Pc，Pm。

4)退火策略。

对于本文算法而言，以遗传算法为主，用模拟退火算法来改进遗传算法的局部搜索能力，使得待求问题能快速搜索到最优解。遗传算法执行完遗传操作后，得到子代种群，而子代种群由于退火策略的引入不能以全概率进入新一代的种群中，为此，以状态i和新状态j为连续的两种状态为例说明，当新状态j的适应度值f(j)小于或等于f(i)时，则直接进入新种群中;当f(j)大于f(i)时，需按照Metropolis准则来确定是否进入新种群中，(6)式给出了新状态j的接受概率

(6)式中:a为退温系数;tk为退火温度。

2.3 算法效率定性分析

虽然理论上SA算法和带最优保存策略的AGA算法能以1的概率搜索到全局最优值，但实际上两者难以实现理论的收敛条件，因此，2种算法的效率和优化性能均不太理想，也导致算法的参数选取困难。综合2种算法的优点，构成自适应遗传退火算法，具有以下优势:1)SA算法在各状态赋予优化过程可变的概率突跳性，高温时，算法具有较高的突跳性，温度渐缓时，Metropolis抽样过程使得SA算法变为几乎是概率为1的带优变异操作，实现了很强的趋化性局部搜索;2)AGA算法采用群体并行搜索机制，而SA算法采用串行搜索，把这两种算法相结合，能够使得SA成为并行搜索算法，以提高算法的优化性能;3)AGA和SA算法对参数的选取要求很苛刻，不合适的参数会严重影响算法的性能。AGA算法的参数选取没有明确的理论指导，多半要靠大量的实验和经验来确定，而AGA和SA相混合，使算法的性能有所提高，因此，对算法参数的选取不必太严格。

3 求解0/1背包问题的自适应遗传退火算法的具体实现

根据以上介绍的算法的各种策略，制定了求解基于0/1背包的自适应遗传退火算法如下。

步骤1 给定算法参数，包括种群规模popsize，染色体长度chromlong，自适应交叉概率Pc1，Pc2，自适应变异概率Pm1，Pm2，退火温度tk，退温系数a等;

步骤2 随机产生初始群体pop(k)，其中k赋初始值0，作为初始迭代;

步骤3 根据适应函数对群体中每一个个体的适应度值作出评价，并判断其是否符合优化准则，若符合，输出最佳个体及其代表的最优解，并结束计算;否则执行以下步骤;

步骤4 按照轮盘赌和最佳保存策略相结合的方式执行选择操作，并按照自适应交叉、变异概率公式执行基因重组和基因突变操作，产生SA算法的初始群体SA_pop(k);

步骤5 从群体SA_pop(k)中的每一染色体i∈SA_pop(k)的领域中随机选取一个状态j∈N(i)，按照Metropolis抽样准则接受或拒绝j，该阶段需要进行popsize次迭代产生下一代群体pop(k+1);

步骤6 执行退温操作tk+1=a×tk，并令k=k+1，返回步骤3;

在自适应遗传退火算法流程中，步骤5的群体选择随机搜索一个个体的领域空间，比单纯遗传算法的搜索空间更大，相当于用N(i)取代了?SA_pop(k)，同时用Metropolis抽样准则由(6)式所确定的接受概率接收可行解，进一步增大了领域内的局部搜索能力，而步骤4中最优保存策略的引入，是为了避免当代种群最优解的流失，同时引入自适应交叉、变异概率，保证了在交叉、变异时能自适应地调整当代种群最佳的Pc，Pm。

4 实例仿真

为了考察AGAA求解0－1背包问题的性能，下面用matlab语言编写了AGAA算法的程序，同时编写了GA，AGA两种算法的程序，3种算法的程序在CPU为Intel cole T6570，内存为2 GByte，操作系统为Window XP的计算机上对4个背包实例进行研究。

4.1 AGAA，AGA和GA的对照实验及结果

实验中，背包数目分别选10，20，50，100为测试实例，其中，实例1来源于文献［6］，实例2和3来自文献［7］，实例4来源于文献［8］。参与对比的2种算法分别为AGA，GA。为了减少随机性对算法性能的影响，各算法对每一测试算例独立运行20次，以便分析它们的统计特征。实验中，3种算法的适应度公式均相同，AGAA，AGA，GA 3种算法的种群规模均选为100，交叉、变异率均设定为 Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.001，AGAA 算法中初始退火温度均设定为800，衰减因子设定为K=0.95，3种算法均以最大迭代次数为停止准则，即背包数目10，20，50，100 分别设定最大迭代次数为 50，80，250，300。

3种算法所获得的统计值比较如表1所示。表1中，性能比较标准为算法在20次独立运行中所获得的最优适应度值Vmax，最差适应度值Vmin，平均适应度值Vavg，平均波动率δ，最小迭代次数Tmin，平均迭代次数Tavg以及所获得可行最优解的次数Z。表1中，N表示不同的背包数目;“—”表示文献中未进行该数值结果的统计;Tmin，Tavg能够衡量算法的收敛速度(时间复杂度);Vmax，Vmin，Vavg，Z 能够衡量算法的寻优能力;δ能够衡量算法的稳定程度。其中

(7)式中，Vopitimation为不同背包数目的理论最优值。

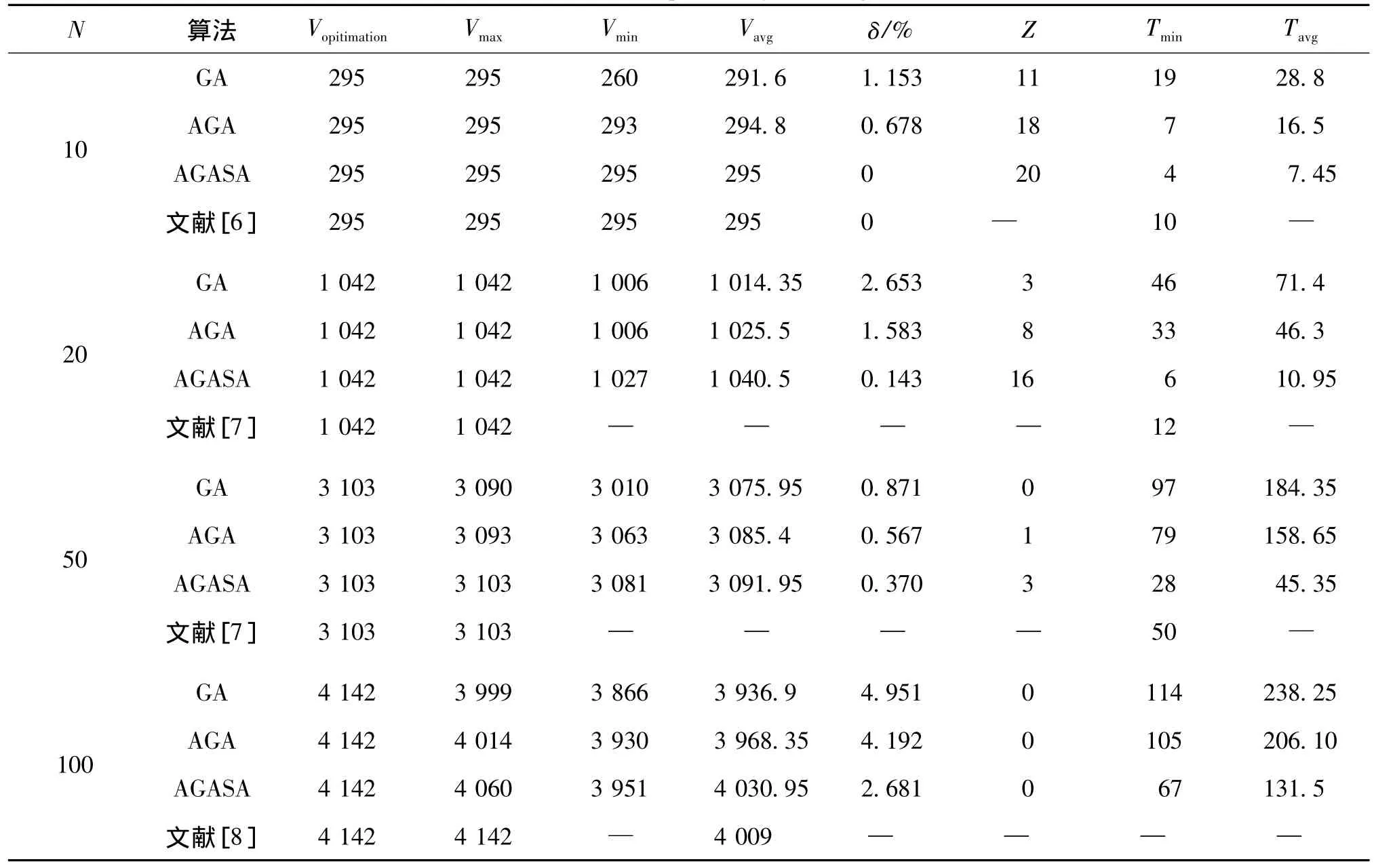
表1 3种算法所获得的统计值比较Tab.1 Statistical comparison by three algorithms

由表1可知，对于10个数目的背包而言，平均波动率均大于0，表明AGA，GA 2种算法在20次独立运行中至少有一次获得了近似最优解;对于20个数目的背包而言，AGAA所获得的最优值数目均比其他2种算法多，且平均波动率为0.143%，明显低于其他2种算法，表明AGAA算法的稳定性更好;对于30个数目的背包，GA，AGA 2种算法均未获得最优值，而AGAA获得了3次最优解，可见，在问题规模逐步增大时，参与比较的2种算法搜索到最优值相当困难，且平均波动率也进一步增大，虽AGAA算法的平均波动率达到了0.370%，但仍小于其他2种算法，进而表明，AGAA的稳定性是较好的;对于100个数目的背包而言，3种算法均未收敛到最优值，只是在解的领域空间里获得了近似最优解，但AGAA所获得的平均适应度值最大，且高于文献［8］，可见该算法的寻优能力最好。从整体上看，对于不同数目的背包问题，AGAA算法的收敛代数明显少于其他2种算法的收敛代数，平均波动率也好于其他2种算法，从而表明，AGAA算法在求解大规模背包问题时，其收敛速度、寻优能力和稳定性要比其他2种算法更满意。

图1—2是N分别为20，50时，3种算法独立运行20次中某一次最佳适应度值的收敛曲线图，从图1可以看出，3种算法均能寻优到理想最优值，而AGAA算法的收敛速度明显大于参与比较的2种算法，从图2可以看出，仅AGAA收敛到了理想最优值，而且收敛速度较快。

图1 N=20时，3种算法最佳适应度值收敛图Fig.1 Best fitness value convergence map of three algorithms when N=20

5 结束语

引入自适应交叉、变异和退火策略的AGAA加剧了染色体之间的竞争，提高了收敛速度，同时加强了种群跳出局部最优的能力，实验结果表明，AGAA处理0/1背包问题具有明显的优越性，具有较好的搜索效率。

图2 N=50时，3种算法最佳适应度值收敛图Fig.2 Best fitness value convergence map of three algorithms when N=20

在N=100个背包的实例中，AGAA算法未能搜索到理论最优值，但平均适应度值高于文献［8］，至此，该算法如何在解决高维0/1背包问题中获得更为理想的解，需进一步研究。

［1］何小锋，马良.求解0-1背包问题的量子蚁群算法［J］.计算机工程与应用，2011，47(16):29-31.HE Xiaofeng，MA Liang.Quantumispired ant algorithm for solving 0-1 knapsack problem［J］.Computer Engineering and Application，2011，47(16):29-31.

［2］熊小华，宁爱兵，马良.多目标0-1背包问题的元胞竞争决策算法［J］.计算机应用研究，2010，27(10):3680-3682.XIONG Xiaohua，NING Aibing，MA Liang.Cellular competitive decision algorithm for multi-objrctive 0-1 knapsack problem［J］.Application Research of Computers，2010，27(10):3680-3682.

［3］吴迪，姜永增，宋广军.基于蜂群遗传算法的0-1背包问题［J］.计算机工程与科学，2011，33(5):102-105.WU Di，JIANG Yongzeng，SONG Guangjun.The 0-1 knapsack problem based on the bee-swarm genetic algorithm［J］.Engineering and Science，2011，33(5):102-105.

［4］黄凯，茅永兴，周文晋.基于遗传算法的测量船工况优选方法［J］.电讯技术，2009，49(7):13-17.HUANG Kai，MAO Yongxing，ZHOU Wenjin.A new method of optimizing the tracking-ship operation condition design based on genetic algorithm［J］.Telecommunication Engineering，2009，49(7):13-17.

［5］李剑，景博.自适应遗传算法在多边多议题协商中的应用［J］.北京邮电大学学报，2008，31(6):67-69.LI Jiang，JING Bo.Adaptive genetic alg-orithm and its application in multi-lateral multi-issue negotiation［J］.Journal of Bei-jing University of Posts and Telecommu-nication，2008，31(6):67-69.

［6］马良，王龙德.背包问题的蚂蚁优化算法［J］.计算机应用，2001，21(8):4-5.MA Niang，WANG Longde.Ant optimization algorithm for knapsack problem［J］.Computer Application，2001，21(8):4-5.

［7］李康顺，贾玉珍，张文生.一种基于模式替代的遗传算法解0/1背包问题［J］.计算机应用研究，2009，26(2):470-471.LI Kangshun，JIA Yuzhen，ZHANG Wensheng.Genetic algorithm with schema raplaced for solving 0/1 knapsack problem［J］.Application Research of Computers，2009，26(2):470-471.

［8］庄中文，钱淑渠.抗体修正免疫算法对高维0/1背包问题的应用［J］.计算机应用研究，2009，26(8):2921-2923.ZHUANG Zhongwen，QIAN Shuqu.Immune algorithm with antibody-repaired and its application for high-dimensional 0/1 knapsack problem［J］.Application Research of Computers，2009，26(8):2921-2923.