与时机判定相结合的关联规则增量更新算法

夏 英，刘晓凤

(重庆邮电大学计算机科学与技术学院，重庆 400065)

0 引言

关联规则是数据挖掘领域中的一个重要研究内容，在电信业务、零售业交易、环境监测、工业生产、互联网服务等领域中应用广泛。随着高速数据获取、网络通信、数据管理等技术的高速发展，时效性高、动态变化的数据不断聚集，隐藏在其中的关联规则也必然会发生变化，及时高效的关联规则更新对于趋势分析、指挥调度、辅助决策、信息推荐等具有重要的应用价值。

近年来，已有许多学者开展了增量式关联规则挖掘的研究，提出了相应的更新算法［1-5］。比如，基于树结构的关联规则更新算法［1-3］，由于算法在发现频繁项集过程中，不需要产生候选项集，因此在挖掘长频繁项集时，具有较高的效率。张根香等［4］提出了基于免疫优化的遗传算法(immune optimization based genetic algorithm，IOGA)，引入遗传算法解决大规模数据集的关联规则增量更新问题。夏英等［5］提出了基于滑动窗口的关联规则增量式更新算法(incremental updating algorithm based on slidingwindow，SWIUA)，该算法基于滑动窗口进行数据更新，挖掘出用户感兴趣的近期的关联规则。以上算法虽然一定程度上提高了关联规则更新算法的效率，但是大多没有考虑关联规则更新时机的问题，直接将其用于实时环境中的模式更新，容易造成不必要的模式更新，同时频繁进行关联规则更新耗费的系统资源较大。针对实时应用中频繁更新的数据集，丁虎［6］提出基于抽样技术的算法(sampling algorithm，SA)，该算法考虑了关联规则更新时机，适合于频繁更新数据时模式更新的情况。但该算法在判定更新时机时需要对新增数据集进行多次扫描，在关联规则更新时仅利用原频繁项集对候选项集进行修剪，这不利于处理大数据集和长频繁项集。

针对频繁更新的数据集，本文在SA算法的基础上，综合考虑关联规则更新时机判定和关联规则增量更新问题，提出了与时机判定相结合的关联规则增量更新算法。

1 相关定义与性质

定义1 关联规则差异度描述了2个数据集中关联规则差异的大小，主要表现在数据集中频繁项集的差异上，其计算方法［6］为

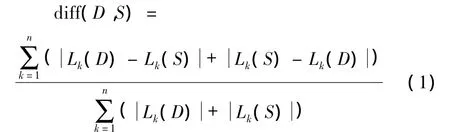
(1)式中:Lk(D)表示数据集D中的频繁k项集;Lk(S)表示数据集 S 中的频繁 k－项集，k=1，2，…，n。

关联规则差异度的取值为［0，1］，0表示2个数据集的关联规则完全相同;1表示2个数据集的关联规则完全不同。计算关联规则差异度可以用于判定关联规则的更新时机，如当关联规则差异度大于阈值¯d时进行关联规则更新，¯d的取值为［0，1］，通常由领域专家或用户所定。

定义2 频繁项集的集合 L={L1，L2，…，Ln}，其中，Ln是频繁n项集，则Ln含有的非空子集个数之和是(2n－2)×mn，其中mn是Ln中频繁项集的个数，对含有非空子集个数之和最多的频繁项集记为LKmax，此时LKmax中频繁项集的长度是Kmax。

Apriori算法是一种常用的关联规则挖掘算法，通常包括连接和剪枝2个步骤，具有“频繁项集的所有非空子集都必须也是频繁的”这一Apriori性质［7］。在关联规则增量更新时，根据定义2计算LKmax，找出其中在更新数据集中仍然频繁的项集，根据Apriori性质，则其对应长度的所有子集也是频繁的，由于这部分子集不需要扫描数据集来判断其频繁性，将其从候选项集中删除，完成对候选项集的修剪。

性质1 如果项集X在原数据集和新增数据集中都是非频繁的，则项集X在更新数据集中是非频繁的，同时项集X的超集也是非频繁的。

对于满足上述条件的候选项集中的项集，根据性质1，则该项集在更新数据集中也不可能是频繁的，可直接从候选项集中删除，从而修剪候选项集。

2 关联规则增量更新算法

关联规则增量更新算法包括更新时机判定和关联规则增量更新2个阶段。根据更新前后数据集的关联规则差异度判定更新时机，如果所得的关联规则差异度大于阈值¯d，则进行关联规则增量更新。

2.1 关联规则更新时机判定方法

针对频繁更新的数据集，以固定时间间隔的方式执行关联规则更新时机判定。在关联规则时机判定阶段，利用已经得到的频繁项集在累积新增数据集中的支持度计数，发现频繁项集，计算关联规则差异度，并以此确定关联规则更新时机，减少对关联规则更新后累积新增数据集的重复扫描，具体过程如下:首先，通过逐层搜索的迭代方法，产生候选项集，然后，扫描本次新增数据集和原始数据集，统计项集支持度计数，发现更新后数据集的频繁项集，进而计算关联规则差异度，最后，确定是否更新关联规则。

根据以上分析，关联规则更新时机判定方法描述如下。

算法1 关联规则更新时机判定方法Updatemoment。

输入:原数据集DB，DB的频繁项集L={L1，L2，…，Ln}，关联规则更新后累积新增数据集db'，本次新增数据集db，最小支持度min_sup，关联规则差异度阈值 ¯d。

输出:是否更新关联规则的布尔值。

Function Updatemoment(DB，L，db'，db，min_sup，¯d)

处理步骤:

2.2 关联规则增量更新算法

本文提出的关联规则增量更新算法，根据上述提出的关联规则时机判定方法，确定是否需要更新关联规则，如果不需要就将原频繁项集作为新频繁项集直接返回;相反，则进行关联规则的更新操作。

在关联规则增量更新阶段，首先对原数据集中频繁项集L根据定义2，求出含有子集个数最多的LKmax，扫描新增数据集，找出LKmax中项集在更新数据集中仍然频繁的项集组成L'Kmax，将L'Kmax的子集直接放入对应长度的新频繁项集 L1'，L2'，…，LK'max－1中。然后计算新频繁i项集(1≤i≤Kmax－1)，通过逐层搜索迭代的方法产生候选项集，把候选项集分成3个互不相交的子集:①L'Kmax的i项子集;②Li－Li'中的项集，即项集在原数据集中是频繁项集，但是它的Kmax项超集不在L'Kmax中;③原数据集中的非频繁项集。对①中的项集，根据Apriori性质，直接把项集加入新频繁项集中，同时将其从候选项集中删除。对②中的项集，扫描新增数据集，即可判断项集在更新数据集中的频繁性，同时将其也从候选项集中删除。对③中的项集，由于其在原始数据集中是非频繁的，基于性质1进行修剪，将修剪之后的其余项集通过扫描更新数据集，即可判断该项集是否是频繁的。最后计算更新数据集中i项(iKmax)新频繁集。

根据以上分析，本文的关联规则增量更新算法描述如下。

算法2 关联规则增量更新算法

输入:原数据集DB，DB的频繁项L={L1，L2，…，Ln}，关联规则更新后累积新增数据集db'，本次新增数据集db，最小支持度min_sup，关联规则差异度阈值 ¯d。

输出:更新数据集 DB'=DB∪db'∪db的频繁项集 L'。

处理步骤:

设原数据集事务数为N，新增数据集事务数为m，频繁项集的最大长度为n，含有子集个数之和最大的频繁项集的长度为k。在关联规则更新时机判定阶段，由于需要扫描原数据集一次，扫描新增数据集n次，确定关联规则差异度，算法的时间复杂度为O(nm+N);在关联规则增量更新阶段，在最好的情况下，新频繁i－项集(ik)可由Apriori性质全部得到，为了得到更新后数据集的新频繁项集，需要扫描原数据集(n－k+1)次，扫描新增数据集(n－k+1)次，此时算法的时间复杂度为O((n－k+1)(N+m));最坏的情况下，为了得到新频繁项集，需要扫描原数据集n次，扫描新增数据集n次，此时算法的时间复杂度为O(n(N+m));因此，完成一次有效的关联规则增量更新，其时间复杂度为O(nm+N+(2n－k+1)(N+m)/2)。对于长频繁项集，k比较接近n，算法时间复杂度为O(nm+N+(n+1)(N+m)/2)。

从算法占有的存储空间上来讲，算法处理过程中，根据Apriori性质，把频繁项集的子集直接放入频繁项集中，减少子集计数计算对存储空间的需求，实现对候选项集的修剪，最终降低了算法对存储空间的需求。

3 实验结果及分析

为了验证本文提出算法的有效性，实验将本文所提出的算法和SA算法使用相同的数据集进行比较。实验对算法的执行时间和计算过程中需要存储的候选项集数量2个指标进行评测。实验使用的环境为Intel(R)CPU 2140@1.60GHz 2.00GB RAM，操作系统为Windows XP Professional，算法使用E-clipse平台的 Java语言实现，数据库选用MySQL5.0。数据集由 IBM QUEST［8］生成，采用的原数据集包含10 000条事务，每次新增的数据集包含1 000条事务。实验中事务的平均长度是20，频繁项集的数量为1 500，最大的潜在频繁项集的平均长度为8。

实验1:测试数据集相同，在不同的最小支持度条件下对比算法的执行时间。设定关联规则差异度阈值¯d为2%，新增数据集的大小为4 000，结果如图1所示。

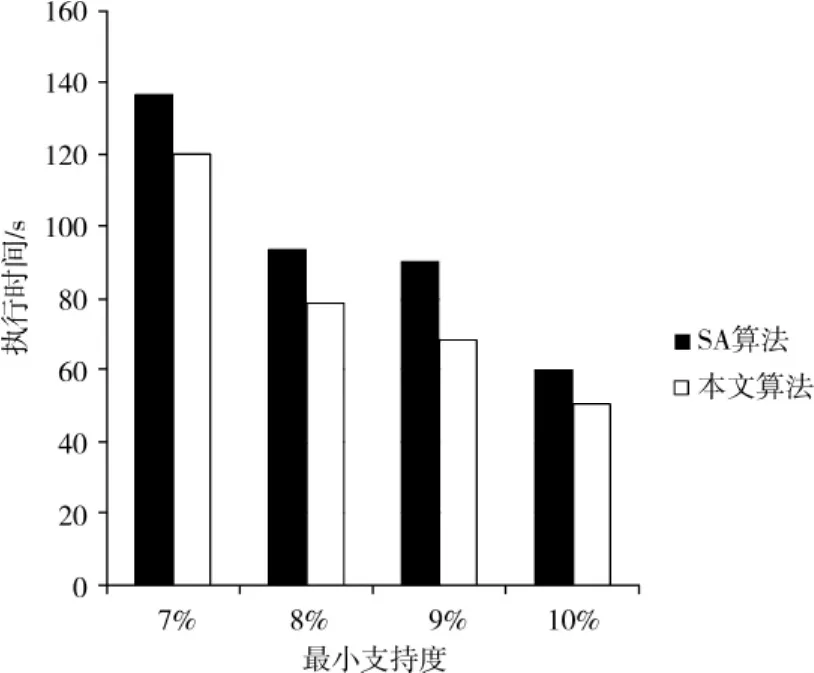
图1 不同最小支持度下算法的执行时间Fig.1 Execution time under the different minimum support

由图1可以看出，随着最小支持度的增大，本文算法的执行时间低于SA算法。原因主要有以下2点:①本文算法在关联规则更新时机判定阶段，利用了频繁项集在累积新增数据集中的支持度计数，可以减少对累积新增数据集的扫描次数;②在关联规则增量更新阶段，本文算法基于Apriori性质直接得到频繁的子集，采用增强的剪枝方法，对候选项集进行修剪，减少对候选项集计算的时间。随着最小支持度的增大，2个算法执行时间都逐渐降低，主要是由于最小支持度决定了产生频繁项集的数量。

实验2:测试数据集相同，在不同的最小支持度条件下对比算法的候选项集数量。设定关联规则差异度阈值¯d为2%，新增数据集的大小为4 000，结果如图2所示。

通过图2可以看出，本文算法的候选项集个数少于SA算法，这是因为本文算法在计算过程中利用Apriori性质，采用增强的剪枝方法，有效的对候选项集进行了修剪，而SA算法在计算的过程中，只是简单利用原频繁项集对候选项集进行修剪。在不损失频繁模式信息的情况下，如果候选项集的个数越少，则算法需要占用的存储空间越少。因此，与SA算法相比，本文算法需要占用较少的存储空间。

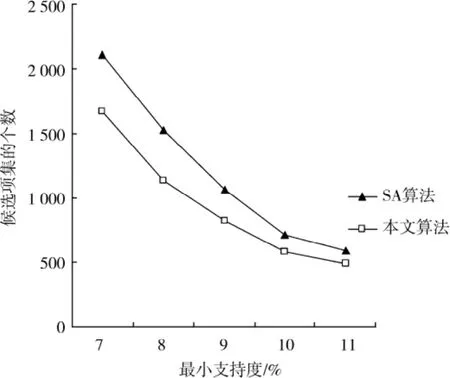
图2 不同最小支持度下算法的候选项集数量Fig.2 Number of candidate itemsets under the different minimum support

4 结论

针对实时应用中的模式增量更新问题，本文提出了与时机判定相结合的关联规则增量更新算法，结合更新时机进行模式更新，同时采用增强的剪枝策略，从而实现关联规则的高效更新。该算法不但可以满足用户的关联规则增量更新要求，而且避免了关联规则更新频繁、更新时间长的这些缺点。目前，本文主要针对数据增加时的关联规则增量更新算法研究，进一步工作还将考虑数据删除或者最小支持度变化时的关联规则更新算法。

［1］LIU Jian-ping，WANG Ying，YANG Fan-ding.Incremental Mining Algorithm Pre-FP in Association Rules Based on FP-tree［C］//Proceedings of Networking and DistributedComputing(ICNDC)，Hangzhou:IEEE Press，2010:199-203.

［2］易彤，徐宝文.一种基于FP树的挖掘关联规则的增量式更新算法［J］.计算机学报，2004，27(5):703-710.YI Tong，XU Baowen.A FP-Tree Based Incremental Updating Algorithm for Mining Association Rules［J］.Chinese Journal of Computers，2004，27(5):703-710.

［3］PRADEEPINI G，JYOTHI S.Tree-based Incremental Association Rule Mining without Candidate Itemset Generation［C］//Proceedings of Trendz in Information Sciences ＆ Computing(TISC)，Chennai:IEEE Press，2010:78-81.

［4］张根香，陈海山.大规模数据集的增量式关联规则挖掘［J］.计算机工程与应用，2009，45(29):120-124.ZHANG Genxiang，CHEN Haishan.Incremental Association Rules Mining for Large Dataset［J］.Computer Engineering and Applications，2009，45(29):120-124.

［5］夏英，刘婉蓉.基于滑动窗口的关联规则增量式更新算法［J］.计算机应用，2008，28(12):3224-3226.XIA Ying，LIU Wanrong.Incremental Updating Algorithm for Association Rule based on Sliding-window［J］.Journal of Computer Applications，2008，28(12):3224-3226.

［6］丁虎.基于数据仓库的关联规则抽样算法研究［D］.哈尔滨:哈尔滨工程大学，2006.DING Hu.The Research of Association Rule Sampling Algorithm Based on Data Warehouse［D］.Harbin:Harbin Engineering University，2006.

［7］JIAWEI H，MICHELINE K.数据挖掘概念与技术［M］.第二版.范明，孟小峰，译.北京:机械工业出版社，2007:148-151.JIAWEI H，MICHELINE K.Data Mining Concepts and Techniques［M］.2nd Edition.FAN Ming，MENG Xiaofeng，translation.BeiJing:Machinery Industry Press，2007:148-151.

［8］CHEUNG D，HAN J，NG V，et al.Maintenance of Discovered Association Rules in Large Databases:An Incremental Updating Technique［C］//Proceedings of the 12th International Conference on Data Engineering，New Orleans:ACM Press，1996:106-114.